8.2: Elementary Matrices and Determinants
- Page ID
- 1998
In chapter 2 we found the elementary matrices that perform the Gaussian row operations. In other words, for any matrix \(M\), and a matrix \(M'\) equal to \(M\) after a row operation, multiplying by an elementary matrix \(E\) gave \(M'=EM\). We now examine what the elementary matrices to do determinants.
Row Swap
Our first elementary matrix multiplies a matrix \(M\) by swapping rows \(i\) and \(j\). Explicitly: let \(R^{1}\) through \(R^{n}\) denote the rows of \(M\), and let \(M'\) be the matrix \(M\) with rows \(i\) and \(j\) swapped. Then \(M\) and \(M'\) can be regarded as a block matrices (where the blocks are rows):
\[ M=\begin{pmatrix}\vdots \\ R^{i} \\ \vdots \\ R^{j} \\ \vdots\end{pmatrix} \textit{ and } M'=\begin{pmatrix}\vdots \\ R^{j} \\ \vdots \\ R^{i} \\ \vdots\end{pmatrix}. \]
Then notice that:
\[M'=\begin{pmatrix} \vdots \\ R^{j} \\ \vdots \\ R^{i} \\ \vdots\\ \\ \end{pmatrix}=
\begin{pmatrix}
1 & & & & & & \\
& \ddots & & & & & \\
& & 0 & & 1 & & \\
& & & \ddots & & & \\
& & 1 & & 0 & & \\
& & & & & \ddots & \\
& & & & & & 1 \\
\end{pmatrix}
\begin{pmatrix} \vdots \\ R^{i} \\ \vdots \\ R^{j} \\ \vdots \\ \\ \end{pmatrix}\]
The matrix
\[
\begin{pmatrix}
1 & & & & & & \\
& \ddots & & & & & \\
& & 0 & & 1 & & \\
& & & \ddots & & & \\
& & 1 & & 0 & & \\
& & & & & \ddots & \\
& & & & & & 1 \\
\end{pmatrix}=:E^{i}_{j}
\]
is just the identity matrix with rows \(i\) and \(j\) swapped. The matrix \(E^{i}_{j}\) is an \(\textit{elementary matrix}\) and
\[ M'=E^{i}_{j}M\, .\]
Because \(\det I=1\) and swapping a pair of rows changes the sign of the determinant, we have found that
\[ \det E^{i}_{j} = -1\, .\]
Now we know that swapping a pair of rows flips the sign of the determinant so \(\det M'=-det M\). But \(\det E_{j}^{i}=-1\) and \(M'=E^{i}_{j} M\) so
\[\det E^{i}_{j} M = \det E^{i}_{j} \, \det M\, .\]
This result hints at a general rule for determinants of products of matrices.
Scalar Multiply
The next row operation is multiplying a row by a scalar. Consider $$M=\begin{pmatrix}R^{1} \\ \vdots \\ R^{n} \end{pmatrix}\, ,$$ where \(R^{i}\) are row vectors. Let \(R^{i}(\lambda)\) be the identity matrix, with the \(i\)th diagonal entry replaced by \(\lambda\), not to be confused with the row vectors. \(\textit{i.e.}\),
\[
R^{i}(\lambda)=
\begin{pmatrix}
1 & & & & \\
& \ddots & & & \\
& & \lambda & & \\
& & & \ddots & \\
& & & & 1 \\
\end{pmatrix}
\, .\]
Then:
\[ M'=R^{i}(\lambda)M=\begin{pmatrix}R^{1} \\ \vdots \\ \lambda R^{i} \\ \vdots \\ R^{n} \end{pmatrix}\, ,\]
equals \(M\) with one row multiplied by \(\lambda\).
What effect does multiplication by the elementary matrix \(R^{i}(\lambda)\) have on the determinant?
\begin{eqnarray*}
\det M' & = & \sum_{\sigma} \textit{sgn}(\sigma) m^{1}_{\sigma(1)}\cdots \lambda m^{i}_{\sigma(i)} \cdots m^{n}_{\sigma(n)} \\
& = & \lambda \sum_{\sigma} \textit{sgn}(\sigma) m^{1}_{\sigma(1)}\cdots m^{i}_{\sigma(i)} \cdots m^{n}_{\sigma(n)} \\
& = & \lambda \det M
\end{eqnarray*}
Thus, multiplying a row by \(\lambda\) multiplies the determinant by \(\lambda\). \(\textit{i.e.,}\) $$\det R^{i}(\lambda) M = \lambda \det M\, .\]

Since \(R^{i}(\lambda)\) is just the identity matrix with a single row multiplied by \(\lambda\), then by the above rule, the determinant of \(R^{i}(\lambda)\) is \(\lambda\). Thus:
\[
\det R^{i}(\lambda) = \det \begin{pmatrix}
1 & & & & \\
& \ddots & & & \\
& & \lambda & & \\
& & & \ddots & \\
& & & & 1 \\
\end{pmatrix} = \lambda\, ,
\]
and once again we have a product of determinants formula:
$$
\det R^{i}(\lambda) M = \det R^{i}(\lambda) \det M
\]
Row Addition
The final row operation is adding \(\mu R^{j}\) to \(R^{i}\). This is done with the elementary matrix \(S^{i}_{j}(\mu)\), which is an identity matrix but with an additional \(\mu\) in the \(i,j\) position:
\[
S^{i}_{j}(\mu) = \begin{pmatrix}
1 & & & & & & \\
& \ddots & & & & & \\
& & 1 & & \mu & & \\
& & & \ddots & & & \\
& & & & 1 & & \\
& & & & & \ddots & \\
& & & & & & 1 \\
\end{pmatrix}\, .
\]
Then multiplying \(M\) by \(S^{i}_{j}(\mu)\) performs a row addition:
\[
\begin{pmatrix}
1 & & & & & & \\
& \ddots & & & & & \\
& & 1 & & \mu & & \\
& & & \ddots & & & \\
& & & & 1 & & \\
& & & & & \ddots & \\
& & & & & & 1 \\
\end{pmatrix}\begin{pmatrix}\\ \vdots \\ R^{i} \\ \vdots \\ R^{j} \\ \vdots\\ \\\end{pmatrix}
=
\begin{pmatrix}\\ \vdots \\ R^{i} +\mu R^{j} \\ \vdots \\ R^{j} \\ \vdots\\ \\ \end{pmatrix}\, .
\]
What is the effect of multiplying by \(S^{i}_{j}(\mu)\) on the determinant? Let \(M'=S^{i}_{j}(\mu)M\), and let \(M''\) be the matrix \(M\) but with \(R^{i}\) replaced by \(R^{j}\). Then
\begin{eqnarray*}
\det M' & = & \sum_{\sigma} \textit{sgn}(\sigma) m^{1}_{\sigma(1)}\cdots (m^{i}_{\sigma(i)}+ \mu m^{j}_{\sigma(j)}) \cdots m^{n}_{\sigma(n)} \\
& = & \sum_{\sigma} \textit{sgn}(\sigma) m^{1}_{\sigma(1)}\cdots m^{i}_{\sigma(i)} \cdots m^{n}_{\sigma(n)} \\
& & \qquad + \sum_{\sigma} \textit{sgn}(\sigma) m^{1}_{\sigma(1)}\cdots \mu m^{j}_{\sigma(j)} \cdots m^{j}_{\sigma(j)} \cdots m^{n}_{\sigma(n)} \\
& = & \det M + \mu \det M''
\end{eqnarray*}
Since \(M''\) has two identical rows, its determinant is \(0\) so
$$
\det M' = \det M,
$$
when \(M'\) is obtained from \(M\) by adding \(\mu\) times row \(j\) to row \(i\).
We also have learnt that
$$\det S^{i}_{j}(\mu)M = \det M\, .$$
Notice that if \(M\) is the identity matrix, then we have $$\det S^{i}_{j}(\mu) = \det (S^{i}_{j}(\mu)I) = \det I = 1\, .\]

Determinant of Products
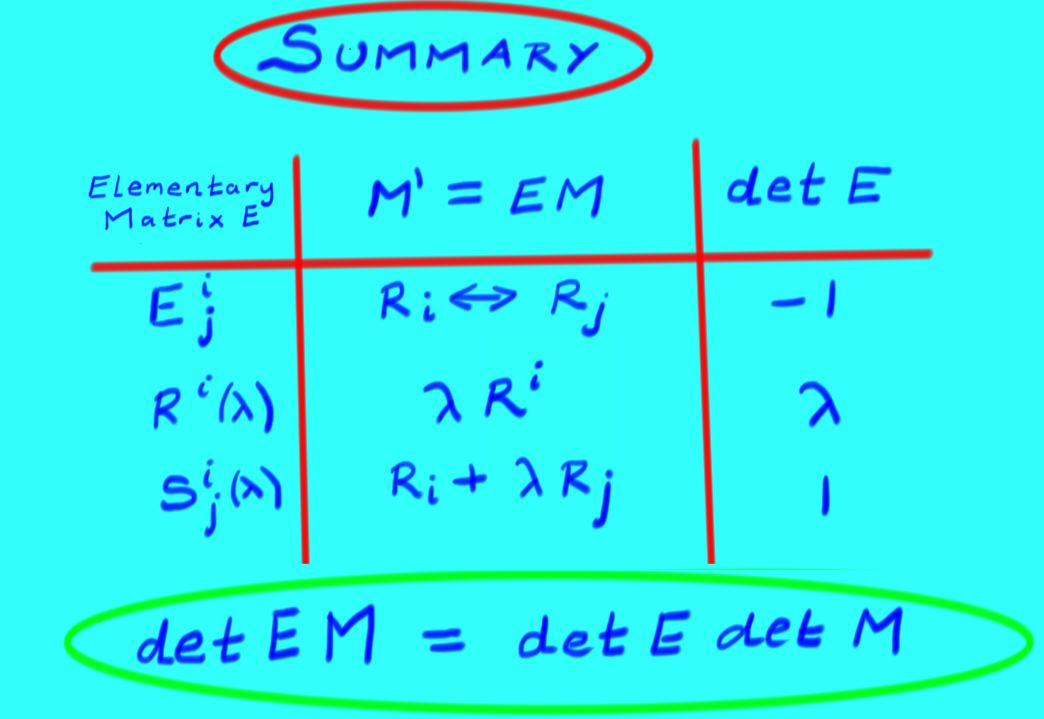
In summary, the elementary matrices for each of the row operations obey
\[
\begin{array}{cccc}
E^{i}_{j} &=& I \textit{ with rows i,j swapped;} &\det E^{i}_{j}=-1 \\
R^{i}(\lambda) &=& I \textit{ with \(\lambda\) in position i,i;}
&\det R^{i}(\lambda)=\lambda \\S^{i}_{j}(\mu) &=& I \textit{ with \mu in position i,j;}
&\det S^{i}_{j}(\mu)=1 \\
\end{array}
\]
Moreover we found a useful formula for determinants of products:
Theorem
If \(E\) is \(\textit{any}\) of the elementary matrices \(E^{i}_{j}, R^{i}(\lambda), S^{i}_{j}(\mu)\), then \(\det(EM)=\det E \det M\).
We have seen that any matrix \(M\) can be put into reduced row echelon form via a sequence of row operations, and we have seen that any row operation can be achieved via left matrix multiplication by an elementary matrix. Suppose that RREF\((M)\) is the reduced row echelon form of \(M\). Then $$RREF(M)=E_{1}E_{2}\cdots E_{k}M\, ,$$ where each \(E_{i}\) is an elementary matrix. We know how to compute determinants of elementary matrices and products thereof, so we ask:
$$\textit{What is the determinant of a square matrix in reduced row echelon form? }$$
The answer has two cases:
1. If \(M\) is not invertible, then some row of \(RREF(M)\) contains only zeros. Then we can multiply the zero row by any constant \(\lambda\) without changing \(M\); by our previous observation, this scales the determinant of \(M\) by \(\lambda\). Thus, if \(M\) is not invertible, \(\det RREF(M)=\lambda \det RREF(M)\), and so \(\det RREF(M)=0\).
2. Otherwise, every row of \(RREF(M)\) has a pivot on the diagonal; since \(M\) is square, this means that \(RREF(M)\) is the identity matrix. So if \(M\) is invertible, \(\det RREF(M)=1\).
Notice that because \(\det RREF(M) = \det (E_{1}E_{2}\cdots E_{k}M)\), by the theorem above, $$\det RREF(M)=\det (E_{1}) \cdots \det (E_{k}) \det M\, .$$ Since each \(E_{i}\) has non-zero determinant, then \(\det RREF(M)=0\) if and only if \(\det M=0\). This establishes an important theorem:
Theorem
\(\textit{For any square matrix M, \det M\neq 0 if and only if M is invertible.}\)
Since we know the determinants of the elementary matrices, we can immediately obtain the following:

Corollary
Any elementary matrix \(E^{i}_{j}, R^i(\lambda), S^{i}_{j}(\mu)\) is invertible, except for \(R^{i}(0)\). In fact, the inverse of an elementary matrix is another elementary matrix.
To obtain one last important result, suppose that \(M\) and \(N\) are square \(n\times n\) matrices, with reduced row echelon forms such that, for elementary matrices \(E_{i}\) and \(F_{i}\), $$M=E_{1}E_{2}\cdots E_{k} \, RREF(M)\, ,$$ and $$N=F_{1}F_{2}\cdots F_{l} \, RREF(N)\, .$$ If \(RREF(M)\) is the identity matrix (\(\textit{i.e.}\), \(M\) is invertible), then:
\begin{eqnarray*}
\det (MN) & = & \det (E_{1}E_{2}\cdots E_{k}\, RREF(M) F_{1}F_{2}\cdots F_{l} \, RREF(N) )\\
& = & \det (E_{1}E_{2}\cdots E_{k} I F_{1}F_{2}\cdots F_{l}\, RREF(N) )\\
& = & \det (E_{1}) \cdots \det(E_{k})\det(I)\det(F_{1})\cdots\det(F_{l})\det RREF(N)\\
& = & \det(M)\det(N)
\end{eqnarray*}
Otherwise, \(M\) is not invertible, and \(\det M=0=\det RREF(M)\). Then there exists a row of zeros in \(RREF(M)\), so \(R^{n}(\lambda)
RREF(M)=RREF(M)\) \(\textit{for any \lambda}\). Then:\begin{eqnarray*}\det (MN) & = & \det (E_{1}E_{2}\cdots E_{k}
\, RREF(M) N )\\
& = & \det (E_{1}E_{2}\cdots E_{k}
\, RREF(M) N )\\
& = & \det (E_{1}) \cdots \det(E_{k})\det(
RREF(M)N)\\
& = & \det (E_{1}) \cdots \det(E_{k})\det( R^{n}(\lambda)
\, RREF(M)N)\\
& = & \det (E_{1}) \cdots \det(E_{k})\lambda \det(
RREF(M)N)\\
& = & \lambda \det (MN)
\end{eqnarray*}
Which implies that \(\det (MN)=0=\det M \det N\).
Thus we have shown that for \(\textit{any}\) matrices \(M\) and \(N\),
\[
\det (MN) = \det M \det N
\]
This result is \(\textit{extremely important}\); do not forget it!

Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


