18.8: Movie Scripts 3-4
- Page ID
- 2194
G.3: Vectors in Space \(n\)-Vectors
Review of Parametric Notation
The equation for a plane in three variables \(x\), \(y\) and \(z\) looks like
$$
ax+by+cz=d
$$
where \(a\), \(b\), \(c\), and \(d\) are constants. Lets look at the example
$$
x+2y+5z=3\, .
$$
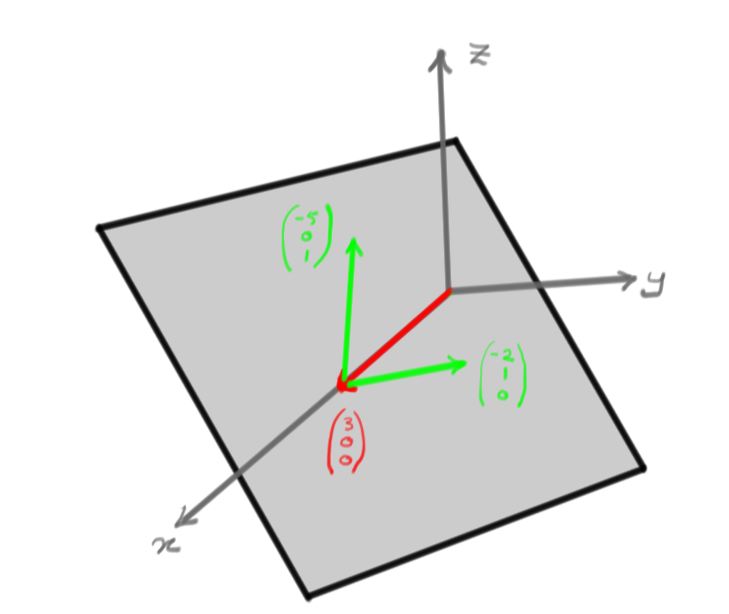
In fact this is a system of linear equations whose solutions form a plane with normal vector \((1,2,5)\). As an augmented matrix the system is simply
$$
\Big( 1 \ \ 2 \ \ 5\ \Big| \ 3 \Big)\, .
$$
This is actually RREF! So we can let \(x\) be our pivot variable and \(y\), \(z\) be represented by free parameters \(\lambda_{1}\) and \(\lambda_{2}\):
$$
x=\lambda_{1}\, , \qquad y = \lambda_{2}\, .
$$
Thus we write the solution as
$$
\begin{array}{ccccc}
x&=&-2\lambda_{1}&-5\lambda_{2}&+3\\
y&=&\lambda_{1}&&\\
z&=&&\lambda_{2}&
\end{array}
$$
or in vector notation
$$
\begin{pmatrix}
x\\y\\z
\end{pmatrix}
=
\begin{pmatrix}
3\\0\\0
\end{pmatrix}
+\lambda_{1}
\begin{pmatrix}
-2\\1\\0
\end{pmatrix}
+\lambda_{2}
\begin{pmatrix}
-5\\0\\1
\end{pmatrix}\, .
$$
This describes a plane parametric equation. Planes are "two-dimensional'' because they are described by two free variables. Here's a picture of the resulting plane:
The Story of Your Life
This video talks about the weird notion of a "length-squared'' for a vector \(v=(x,t)\) given by \(||v||^{2}=x^{2}-t^{2}\) used in Einstein's theory of relativity. The idea is to plot the story of your life on a plane with coordinates \((x,t)\). The coordinate \(x\) encodes \(\textit{where}\) an event happened (for real life situations, we must replace \(x\to (x,y,z)\in \mathbb{R}^{3}\)). The coordinate \(t\) says \(\textit{when}\) events happened. Therefore you can plot your life history as a worldline as shown:

Each point on the worldline corresponds to a place and time of an event in your life. The slope of the worldline has to do with your speed. Or to be precise, the inverse slope is your velocity. Einstein realized that the maximum speed possible was that of light, often called \(c\). In the diagram above \(c=1\) and corresponds to the lines \(x=\pm t\Rightarrow x^{2}-t^{2}=0\). This should get you started in your search for vectors with zero length.
G.4: Vector Spaces
Examples of Each Rule
Lets show that \(\mathbb{R}^{2}\) is a vector space. To do this (unless we invent some clever tricks) we will have to check all parts of the definition. Its worth doing this once, so here we go: Before we start, remember that for \(\mathbb{R}^{2}\) we define vector addition and scalar multiplication component-wise.
- Additive closure: We need to make sure that when we add \(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\) and \(\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}\) that we do not get something outside the original vector space \(\mathbb{R}^{2}\). This just relies on the underlying structure of real numbers whose sums are again real numbers so, using our component-wise addition law we have $$\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} := \begin{pmatrix}x_{1}+x_{2}\\y_{1}+y_{2}\end{pmatrix}\in \mathbb{R}^{2}\, .$$
- Additive commutativity: We want to check that when we add any two vectors we can do so in either order, \(\textit{i.e.}\) $$\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix} + \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} \stackrel?= \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} + \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}.$$ This again relies on the underlying real numbers which for any \(x,y\in \mathbb{R}\) obey $$x+y=y+x\, .$$ This fact underlies the middle step of the following computation $$\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix} + \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} = \begin{pmatrix}x_{1}+y_{1}\\x_{2}+y_{2}\end{pmatrix} = \begin{pmatrix}y_{1}+x_{1}\\y_{2}+x_{2}\end{pmatrix} = \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} + \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$$ which demonstrates what we wished to show.
- Additive Associativity: This shows that we needn't specify with parentheses which order we intend to add triples of vectors because their sums will agree for either choice. What we have to check is $$\left(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}\right)+\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix} \stackrel?= \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\left(\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}+\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}\right)\, .$$ Again this relies on the underlying associativity of real numbers: $$(x+y)+z=x+(y+z)\, .$$ The computation required is $$\left(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}\right)+\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix} = \begin{pmatrix}x_{1}+y_{1}\\x_{2}+y_{2}\end{pmatrix}+\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix} = \begin{pmatrix}(x_{1}+y_{1})+z_{1}\\(x_{2}+y_{2})+z_{2}\end{pmatrix}$$ $$=\begin{pmatrix}x_{1}+(y_{1}+z_{1})\\x_{2}+(y_{2}+z_{2})\end{pmatrix} = \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix}+\begin{pmatrix}y_{1}+z_{1}\\y_{2}+z_{2}\end{pmatrix} = \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+ \left(\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}+\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}\right)\, .$$
- Zero: There needs to exist a vector $\vec 0$ that works the way we would expect zero to behave, \(\textit{i.e.}\) $$\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}+\vec 0=\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}\, .$$ It is easy to find, the answer is $$\vec 0 = \begin{pmatrix}0\\0\end{pmatrix}\, .$$ You can easily check that when this vector is added to any vector, the result is unchanged.
- Additive Inverse: We need to check that when we have \(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\), there is another vector that can be added to it so the sum is \(\vec 0\). (Note that it is important to first figure out what \(\vec 0\) is here!) The answer for the additive inverse of \(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\) is \(\begin{pmatrix}-x_{1}\\-x_{2}\end{pmatrix}\) because $$\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\begin{pmatrix}-x_{1}\\-x_{2}\end{pmatrix} = \begin{pmatrix}x_{1}-x_{1}\\x_{2}-x_{2}\end{pmatrix} = \begin{pmatrix}0\\0\end{pmatrix}=\vec 0\, .$$
We are half-way done, now we need to consider the rules for scalar multiplication. Notice, that we multiply vectors by scalars (\(\textit{i.e.}\) numbers) but do NOT multiply a vectors by vectors.
- Multiplicative closure: Again, we are checking that an operation does not produce vectors outside the vector space. For a scalar \(a\in \mathbb{R}\), we require that \(a\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\) lies in \(\mathbb{R}^{2}\). First we compute using our component-wise rule for scalars times vectors: $$a\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}=\begin{pmatrix}ax_{1}\\ax_{2}\end{pmatrix}.$$ Since products of real numbers \(a x_{1}\) and \(a x_{2}\) are again real numbers we see this is indeed inside \(\mathbb{R}^{2}\).
- Multiplicative distributivity: The equation we need to check is $$(a+b)\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\stackrel?= a\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+b\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}.$$ Once again this is a simple LHS=RHS proof using properties of the real numbers. Starting on the left we have $$(a+b)\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix} = \begin{pmatrix}(a+b)x_{1}\\(a+b)x_{2}\end{pmatrix} = \begin{pmatrix}ax_{1}+b x_{1}\\ax_{2}+bx_{2}\end{pmatrix} \qquad\qquad$$ $$\qquad\qquad=\begin{pmatrix}ax_{1}\\ax_{2}\end{pmatrix}+\begin{pmatrix}b x_{1}\\bx_{2}\end{pmatrix} = a\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+b\begin{pmatrix} x_{1}\\x_{2}\end{pmatrix},$$ as required.
- Additive distributivity: This time we need to check the equation $$a\left(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}\right)\stackrel?=a\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+a\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix},$$ \(\textit{i.e.}\), one scalar but two different vectors. The method is by now becoming familiar $$a\left(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}\right)=a\left(\begin{pmatrix}x_{1}+y_{1}\\x_{2}+y_{2}\end{pmatrix}\right)=\begin{pmatrix}a(x_{1}+y_{1})\\a(x_{2}+y_{2})\end{pmatrix}\qquad$$ $$\qquad\qquad=\begin{pmatrix}ax_{1}+ay_{1}\\ax_{2}+ay_{2}\end{pmatrix}=\begin{pmatrix}ax_{1}\\ax_{2}\end{pmatrix}+\begin{pmatrix}ay_{1}\\ay_{2}\end{pmatrix}=a\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}+a\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix},$$ again as required.
- Multiplicative associativity. Just as for addition, this is the requirement that the order of bracketing does not matter. We need to establish whether $$(a.b)\cdot\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\stackrel?=a\cdot\left(b\cdot \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\right),$$ This clearly holds for real numbers \(a.(b.x)=(a.b).x\). The computation is $$(a.b)\cdot\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}=\begin{pmatrix}(a.b).x_{1}\\(a.b).x_{2}\end{pmatrix}=\begin{pmatrix}a.(b.x_{1})\\a.(b.x_{2})\end{pmatrix}=a.\begin{pmatrix}(b.x_{1})\\(b.x_{2})\end{pmatrix}=a\cdot\left(b\cdot \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\right),$$ which is what we want.
- Unity: We need to find a special scalar acts the way we would expect "1'' to behave. \(\textit{I.e.}\) $$\mbox{"1''}\cdot\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}=\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}.$$ There is an obvious choice for this special scalar---just the real number \(1\) itself. Indeed, to be pedantic lets calculate $$1\cdot\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}=\begin{pmatrix}1.x_{1}\\1.x_{2}\end{pmatrix}=\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}.$$
Now we are done---we have really proven the \(\mathbb{R}^{2}\) is a vector space so lets write a little square \(\square\) to celebrate.
Example of a Vector Space
This video talks about the definition of a vector space. Even though the defintion looks long, complicated and abstract, it is actually
designed to model a very wide range of real life situations. As an example, consider the vector space
$$
V=\{\mbox{all possible ways to hit a hockey puck}\}\, .
$$
The different ways of hitting a hockey puck can all be considered as vectors. You can think about adding vectors by having two players hitting the puck at the same time. This picture shows vectors \(N\) and \(J\) corresponding to the ways Nicole Darwitz and Jenny Potter hit a hockey puck, plus the vector obtained when they hit the puck together.
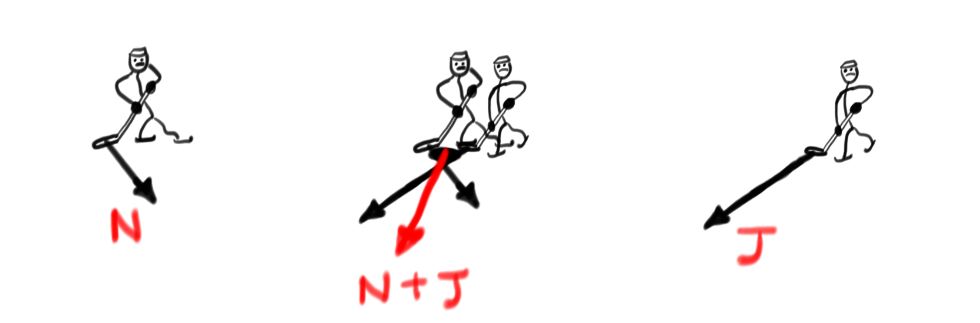
You can also model the new vector \(2J\) obtained by scalar multiplication by \(2\) by thinking about Jenny hitting the puck twice
(or a world with two Jenny Potters....). Now ask yourself questions like whether the multiplicative distributive law $$2J + 2N = 2(J+N)$$
make sense in this context.
Hint for Review Question 5
Lets worry about the last part of the problem. The problem can be solved by considering a non-zero simple polynomial, such as a degree \(0\) polynomial, and multiplying by \(i \in \mathbb{C}\). That is to say we take a vector \(p \in P_{3}^{\mathbb{R}}\) and then considering \(i\cdot p\). This will violate one of the vector space rules about scalars, and you should take from this that the scalar field matters.
As a second hint, consider \(\mathbb{Q}\) (the field of rational numbers). This is not a vector space over \(\mathbb{R}\) since \(\sqrt{2}\cdot 1 = \sqrt{2} \neq \mathbb{Q}\), so it is not closed under scalar multiplication, but it is clearly a vector space over \(\mathbb{Q}\).
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


