1.3: Volume by Cylindrical Shells
- Page ID
- 505
Cylindrical Shells
Consider rotating the region between the curve
\[y = x^2, \nonumber\]
the line
\[x = 2, \nonumber\]
and the x-axis about the y-axis.
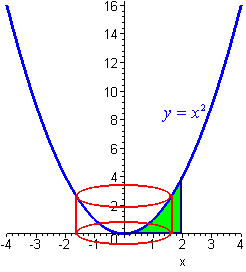
If instead of taking a cross section perpendicular to the y-axis, we take a cross section perpendicular to the x-axis, and revolve it about the y-axis, we get a cylinder. Recall that the area of a cylinder is given by:
\[ A = 2\pi r h \nonumber\]
where \(r\) is the radius of the cylinder and \(h\) is the height of the cylinder. We can see that the radius is the x coordinate of the point on the curve, and the height is the y coordinate of the curve. Hence
\[A(x) = 2\pi xy = 2\pi x(x^2). \nonumber\]
Therefore the volume is given by
\[ \begin{align*} \text{Volume} &= 2\pi \int_{0}^{1} x^3 dx \\ &= \dfrac{\pi}{2}. \end{align*} \]
Example 1
Find the volume of revolution of the region bounded by the curves
- \(y = x^2 + 2\)
- \(y = x + 4\)
- and the y-axis
about the y-axis.
Solution
We draw the picture with a cross section perpendicular to the x-axis.
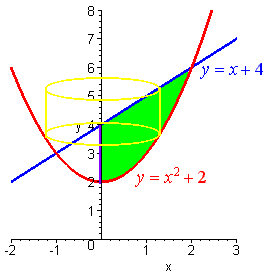
The radius of the cylinder is \(x\) and the height is the difference of the \(y\) coordinates:
\[h = (x + 4) - (x^2 + 2). \nonumber\]
We solve for \(b\).
\[\begin{align*} (x+4)&=(x^2+2) \\ x^2-x-2&=0 \\ (x-2)(x+1)&=0 \end{align*} \]
So that \(b = 2\). Hence the volume is equal to
\[\begin{align*} 2 \pi \int_{0}^{2} \big[ (x+4) -(x^2+2) \big] dx &= 2 \pi \int_{0}^{2}(x^2+2x-x^3) dx \\ &= 2 \pi \left(\dfrac{x^3}{3}+x^2-\dfrac{x^4}{4} \right]_{0}^{2} \\ &= 2 \pi \Big( \dfrac{8}{3}+4 -4 \Big) \\ &= \dfrac{16 \pi}{3}. \end{align*} \]
Exercises
- \(y=x^2-3x+2\), \(y=0 \) about the y-axis
- \(y=x^2-7x+6\), \(y=0 \) about the y-axis
- \(x=1-y^2 \), \(x=0 \) (first quadrant) about the x-axis
- \(y=x\sqrt{1+x^3}\), \(y=0\), \(x=2 \) about the y-axis
- \((x-1)^2+y^2=1\) about the y-axis
- \(x^2+(y-1)^2=1\) about the x-axis
- \(y=x^2-2x+1\), \(y=1\) about the line \(x=3\)
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


