2.1: Vector Valued Functions
- Page ID
- 593
Definition of a Vector Valued Function
A vector valued function is a function where the domain is a subset of the real numbers and the range is a vector.
In two dimensions
\[\textbf{r}(t)=x(t)\hat{\textbf{i}}+y(t) \hat{\textbf{j}}. \]
In three dimensions
\[ \textbf{ r}(t)=x(t)\hat{\textbf{i}}+y(t) \hat{\textbf{j}}+ z(t) \hat{\textbf{k}}. \]
You will notice the strong resemblance to parametric equations. In fact there is an equivalence between vector valued functions and parametric equations.
Example \(\PageIndex{1}\)
\[ \textbf{ r}(t)=3\hat{\textbf{i}}+t\hat{\textbf{j}} +(\sin t) \hat{\textbf{k}} \]
To graph a vector valued function we can just graph the parametrically defined function.
For more information click here
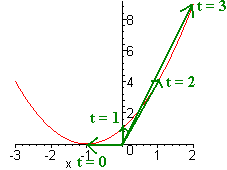
Example \(\PageIndex{2}\)
Sketch the graph of
\[ \textbf{ r}(t)=(t-1)\hat{\textbf{i}}+t^2 \hat{\textbf{j}} \]
Solution
We draw vectors for several values of t and connect the dots. Notice that the graph is the same as \(y=(x+1)^2 \).
Limits
We define the limit of a vector valued function by taking the limit of each of the components. Formally
Definition: Limit of a Vector Valued Function
\[\lim_{t\to{t_0}} \textbf{r}(t) = (\lim_{t\to{t_0}} x(t)) \hat{\textbf{i}} + (\lim_{t\to{t_0}} y(t)) \hat{\textbf{j}} + (\lim_{t\to{t_0}} z(t)) \hat{\textbf{k}}.\]
Example \(\PageIndex{3}\)
Find the limit
\[\lim_{t\to{0}} r(t)\]
if
\[ \textbf{r}=e^t \hat{\textbf{i}} + \dfrac{\sin t}{t} \hat{\textbf{j}} + (t \ln t ) \hat{\textbf{k}}. \]
Solution
We take the three limits one at a time
The first function is continuous at \(t = 0\), so we can just plug in to get
\[e^0 =1. \]
For the second function, we get 0/0, so we use L'Hospital's rule to get
\[ \dfrac{\cos t}{1}. \]
Now plug in to get
\[\dfrac{1}{1}=1. \]
For the \(k^{\text{th}}\) component, we rewrite as
\[ \dfrac{\ln t}{\frac{1}{t}}. \]
Now use L'Hospital's rule to get
\[ \dfrac{\frac {1}{t}}{-\frac{1}{t^2}}=t. \]
Plugging in 0 gives 0. Finally, gathering our results gives a limit of
\[ \hat{\textbf{i}} + \hat{\textbf{j}}. \]
Continuity
We define continuity of vector valued functions in a similar way to how continuity of real valued functions was defined.
Definition: Continuous Functions
A vector valued function is continuous at \(t_0\) if it is defined at \(t_0\) and
\[ \lim_{t\to{t_0}} r(t)=r(t_0). \]
The practical way to investigate continuity is to look at each of the components.
Example \(\PageIndex{4}\)
Determine where the following vector valued function is continuous.
\[ \textbf{r} (t) = \ln (1-t) \hat{\textbf{i}} + \dfrac{1}{t} \hat{\textbf{j}} + 3t \hat{\textbf{k}}. \]
Solution
The first component is continuous for all values of \(t\) less than 1, the second component is continuous for \(t\) nonzero, and the third component is continuous for all real numbers. We can conclude that \(\textbf{r} (t)\) is continuous for all \(t\) less than 1 but not equal to 0.
Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.

