6.1: Exponential Functions
- Page ID
- 1286
- Evaluate exponential functions.
- Find the equation of an exponential function.
- Use compound interest formulas.
- Evaluate exponential functions with base \(e\).
India is the second most populous country in the world with a population of about \(1.25\) billion people in 2013. The population is growing at a rate of about \(.2\%\) each year. If this rate continues, the population of India will exceed China’s population by the year 2031. When populations grow rapidly, we often say that the growth is “exponential,” meaning that something is growing very rapidly. To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.
When exploring linear growth, we observed a constant rate of change—a constant number by which the output increased for each unit increase in input. For example, in the equation \(f(x)=3x+4\), the slope tells us the output increases by \(3\) each time the input increases by \(1\). The scenario in the India population example is different because we have a percent change per unit time (rather than a constant change) in the number of people.
Defining an Exponential Function
A study found that the percent of the population who are vegans in the United States doubled from 2009 to 2011. In 2011, \(2.5\%\) of the population was vegan, adhering to a diet that does not include any animal products—no meat, poultry, fish, dairy, or eggs. If this rate continues, vegans will make up \(10\%\) of the U.S. population in 2015, \(40\%\) in 2019, and \(80\%\) in 2050.
What exactly does it mean to grow exponentially? What does the word double have in common with percent increase? People toss these words around errantly. Are these words used correctly? The words certainly appear frequently in the media.
- Percent change refers to a change based on a percent of the original amount.
- Exponential growth refers to an increase based on a constant multiplicative rate of change over equal increments of time, that is, a percent increase of the original amount over time.
- Exponential decay refers to a decrease based on a constant multiplicative rate of change over equal increments of time, that is, a percent decrease of the original amount over time.
For us to gain a clear understanding of exponential growth, let us contrast exponential growth with linear growth. We will construct two functions. The first function is exponential. We will start with an input of \(0\), and increase each input by \(1\). We will double the corresponding consecutive outputs. The second function is linear. We will start with an input of \(0\), and increase each input by \(1\). We will add \(2\) to the corresponding consecutive outputs (Table \(\PageIndex{1}\)).
From Table \(\PageIndex{1}\) we can infer that for these two functions, exponential growth dwarfs linear growth.
- Exponential growth refers to the original value from the range increases by the same percentage over equal increments found in the domain.
- Linear growth refers to the original value from the range increases by the same amount over equal increments found in the domain.
| \(x\) | \(f(x)=2^x\) | \(g(x)=2x\) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 8 | 6 |
| 4 | 16 | 8 |
| 5 | 32 | 10 |
| 6 | 64 | 12 |
Apparently, the difference between “the same percentage” and “the same amount” is quite significant. For exponential growth, over equal increments, the constant multiplicative rate of change resulted in doubling the output whenever the input increased by one. For linear growth, the constant additive rate of change over equal increments resulted in adding \(2\) to the output whenever the input was increased by one.
The general form of the exponential function is \(f(x)=ab^x\), where \(a\) is any nonzero number, \(b\) is a positive real number not equal to \(1\).
- If \(b>1\),the function grows at a rate proportional to its size.
- If \(0<b<1\), the function decays at a rate proportional to its size.
Let’s look at the function \(f(x)=2^x\) from our example. We will create a table (Table \(\PageIndex{2}\)) to determine the corresponding outputs over an interval in the domain from \(−3\) to \(3\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(2^{−3}=\dfrac{1}{8}\) | \(2^{−2}=\dfrac{1}{4}\) | \(2^{−1}=\dfrac{1}{2}\) | \(2^0=1\) | \(2^1=2\) | \(2^2=4\) | \(2^3=8\) |
Let us examine the graph of \(f\) by plotting the ordered pairs from Table \(\PageIndex{2}\) and then make a few observations \(\PageIndex{1}\).

Let’s define the behavior of the graph of the exponential function \(f(x)=2^x\) and highlight some its key characteristics.
- the domain is \((−\infty,\infty)\),
- the range is \((0,\infty)\),
- as \(x\rightarrow \infty\), \(f(x)\rightarrow \infty\),
- as \(x\rightarrow −\infty\), \(f(x)\rightarrow 0\),
- \(f(x)\) is always increasing,
- the graph of \(f(x)\) will never touch the x-axis because base two raised to any exponent never has the result of zero.
- \(y=0\) is the horizontal asymptote.
- the y-intercept is \(1\).
For any real number \(x\),an exponential function is a function with the form
\[f(x)=ab^x\]
where
- \(a\) is a non-zero real number called the initial value and
- \(b\) is any positive real number such that \(b≠1\).
- The domain of \(f\) is all real numbers.
- The range of \(f\) is all positive real numbers if \(a>0\).
- The range of \(f\) is all negative real numbers if \(a<0\).
- The y-intercept is \((0,a)\),and the horizontal asymptote is \(y=0\).
Which of the following equations are not exponential functions?
- \(f(x)=4^{3(x−2)}\)
- \(g(x)=x^3\)
- \(h(x)=\left(\dfrac{1}{3}\right)^x\)
- \(j(x)=(−2)^x\)
Solution
By definition, an exponential function has a constant as a base and an independent variable as an exponent. Thus, \(g(x)=x^3\) does not represent an exponential function because the base is an independent variable. In fact, \(g(x)=x^3\) is a power function.
Recall that the base \(b\) of an exponential function is always a positive constant, and \(b≠1\). Thus, \(j(x)={(−2)}^x\) does not represent an exponential function because the base, \(−2\), is less than \(0\).
Which of the following equations represent exponential functions?
- \(f(x)=2x^2−3x+1\)
- \(g(x)={0.875}^x\)
- \(h(x)=1.75x+2\)
- \(j(x)={1095.6}^{−2x}\)
- Answer
-
\(g(x)={0.875}^x\) and \(j(x)={1095.6}^{−2x}\) represent exponential functions.
Evaluating Exponential Functions
Recall that the base of an exponential function must be a positive real number other than \(1\).Why do we limit the base bb to positive values? To ensure that the outputs will be real numbers. Observe what happens if the base is not positive:
- Let \(b=−9\) and \(x=\dfrac{1}{2}\). Then \(f(x)=f\left(\dfrac{1}{2}\right)={(−9)}^{\dfrac{1}{2}}=\sqrt{−9}\),which is not a real number.
Why do we limit the base to positive values other than \(1\)? Because base \(1\) results in the constant function. Observe what happens if the base is \(1\):
- Let \(b=1\). Then \(f(x)=1^x=1\) for any value of \(x\).
To evaluate an exponential function with the form \(f(x)=b^x\),we simply substitute \(x\) with the given value, and calculate the resulting power. For example:
Let \(f(x)=2^x\). What is \(f(3)\)?
\[\begin{align*} f(x)&= 2^x\\ f(3)&= 2^3 \qquad \text{Substitute } x=3\\ &= 8 \qquad \text{Evaluate the power} \end{align*}\]
To evaluate an exponential function with a form other than the basic form, it is important to follow the order of operations. For example:
Let \(f(x)=30{(2)}^x\). What is \(f(3)\)?
\[\begin{align*} f(x)&= 30{(2)}^x\\ f(3)&= 30{(2)}^3 \qquad \text{Substitute } x=3\\ &= 30(8) \qquad \text{Simplify the power first}\\ &= 240 \qquad \text{Multiply} \end{align*}\]
Note that if the order of operations were not followed, the result would be incorrect:
\[f(3)=30{(2)}^3≠{60}^3=216,000 \nonumber\]
Let \(f(x)=5{(3)}^{x+1}\). Evaluate \(f(2)\) without using a calculator.
Solution
Follow the order of operations. Be sure to pay attention to the parentheses.
\[\begin{align*} f(x)&= 5{(3)}^{x+1}\\ f(2)&= 5{(3)}^{2+1} \qquad \text{Substitute } x=2\\ &= 5{(3)}^3 \qquad \text{Add the exponents}\\ &= 5(27) \qquad \text{Simplify the power}\\ &= 135 \qquad \text{Multiply} \end{align*}\]
Let \(f(x)=8{(1.2)}^{x−5}\). Evaluate \(f(3)\) using a calculator. Round to four decimal places.
- Answer
-
\(5.5556\)
Defining Exponential Growth
Because the output of exponential functions increases very rapidly, the term “exponential growth” is often used in everyday language to describe anything that grows or increases rapidly. However, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.
A function that models exponential growth grows by a rate proportional to the amount present. For any real number \(x\) and any positive real numbers \(a\) and \(b\) such that \(b≠1\),an exponential growth function has the form
\[f(x)=ab^x\]
where
- \(a\) is the initial or starting value of the function.
- \(b\) is the growth factor or growth multiplier per unit \(x\).
In more general terms, we have an exponential function, in which a constant base is raised to a variable exponent. To differentiate between linear and exponential functions, let’s consider two companies, A and B. Company A has \(100\) stores and expands by opening \(50\) new stores a year, so its growth can be represented by the function \(A(x)=100+50x\). Company B has \(100\) stores and expands by increasing the number of stores by \(50\%\) each year, so its growth can be represented by the function \(B(x)=100{(1+0.5)}^x\).
A few years of growth for these companies are illustrated in Table \(\PageIndex{3}\).
| Year, \(x\) | Stores, Company A | Stores, Company B |
|---|---|---|
| \(0\) | \(100+50(0)=100\) | \(100{(1+0.5)}^0=100\) |
| \(1\) | \(100+50(1)=150\) | \(100{(1+0.5)}^1=150\) |
| \(2\) | \(100+50(2)=200\) | \(100{(1+0.5)}^2=225\) |
| \(3\) | \(100+50(3)=250\) | \(100{(1+0.5)}^3=337.5\) |
| \(x\) | \(A(x)=100+50x\) | \(B(x)=100{(1+0.5)}^x\) |
The graphs comparing the number of stores for each company over a five-year period are shown in Figure \(\PageIndex{2}\). We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
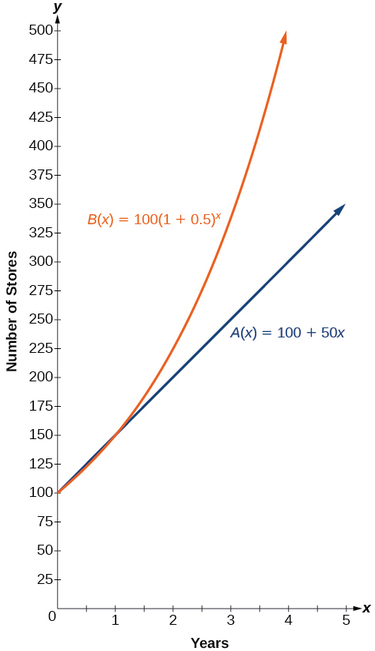
Notice that the domain for both functions is \([0,\infty)\),and the range for both functions is \([100,\infty)\). After year 1, Company B always has more stores than Company A.
Now we will turn our attention to the function representing the number of stores for Company \(B\), \(B(x)=100{(1+0.5)}^x\). In this exponential function, \(100\) represents the initial number of stores, \(0.50\) represents the growth rate, and \(1+0.5=1.5\) represents the growth factor. Generalizing further, we can write this function as \(B(x)=100{(1.5)}^x\),where \(100\) is the initial value, \(1.5\) is called the base, and \(x\) is called the exponent.
At the beginning of this section, we learned that the population of India was about \(1.25\) billion in the year 2013, with an annual growth rate of about \(1.2\%\). This situation is represented by the growth function \(P(t)=1.25{(1.012)}^t\), where \(t\) is the number of years since 2013. To the nearest thousandth, what will the population of India be in 2031?
Solution
To estimate the population in 2031, we evaluate the models for \(t=18\), because 2031 is \(18\) years after 2013. Rounding to the nearest thousandth,
\[P(18)=1.25{(1.012)}^{18}≈1.549 \nonumber\]
There will be about \(1.549\) billion people in India in the year 2031.
The population of China was about \(1.39\) billion in the year 2013, with an annual growth rate of about \(0.6\%\). This situation is represented by the growth function \(P(t)=1.39{(1.006)}^t\), where \(t\) is the number of years since 2013.To the nearest thousandth, what will the population of China be for the year 2031? How does this compare to the population prediction we made for India in Example \(\PageIndex{3}\)?
- Answer
-
About \(1.548\) billion people; by the year 2031, India’s population will exceed China’s by about \(0.001\) billion, or \(1\) million people.
Finding Equations of Exponential Functions
In the previous examples, we were given an exponential function, which we then evaluated for a given input. Sometimes we are given information about an exponential function without knowing the function explicitly. We must use the information to first write the form of the function, then determine the constants \(a, a\) and \(b, b\),and evaluate the function.
- If one of the data points has the form \((0,a)\), then \(a\) is the initial value. Using \(a\), substitute the second point into the equation \(f(x)=a{(b)}^x\), and solve for \(b\).
- If neither of the data points have the form \((0,a)\), substitute both points into two equations with the form \(f(x)=a{(b)}^x\). Solve the resulting system of two equations in two unknowns to find \(a\) and \(b\).
- Using the \(a\) and \(b\) found in the steps above, write the exponential function in the form \(f(x)=a{(b)}^x\).
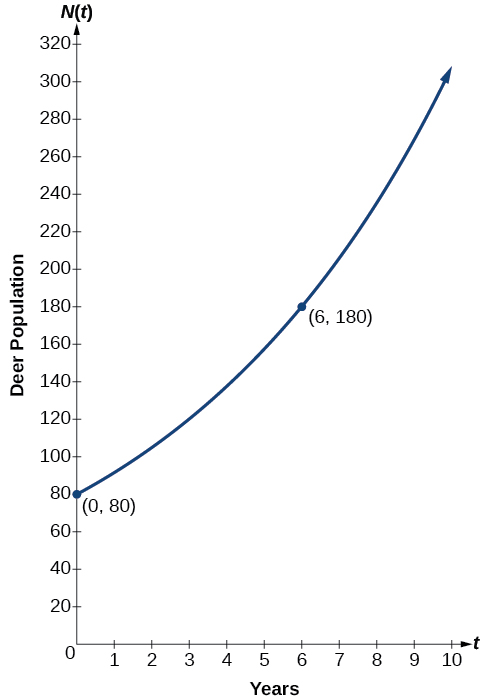
In 2006, \(80\) deer were introduced into a wildlife refuge. By 2012, the population had grown to \(180\) deer. The population was growing exponentially. Write an algebraic function \(N(t)\) representing the population \((N)\) of deer over time \(t\).
Solution
We let our independent variable \(t\) be the number of years after 2006. Thus, the information given in the problem can be written as input-output pairs: (0, 80) and (6, 180). Notice that by choosing our input variable to be measured as years after 2006, we have given ourselves the initial value for the function, \(a=80\). We can now substitute the second point into the equation \(N(t)=80b^t\) to find \(b\):
\[\begin{align*} N(t)&= 80b^t\\ 180&= 80b^6 \qquad \text{Substitute using point } (6, 180)\\ \dfrac{9}{4}&= b^6 \qquad \text{Divide and write in lowest terms}\\ b&= {\left (\dfrac{9}{4} \right )}^{\tfrac{1}{6}} \qquad \text{Isolate b using properties of exponents}\\ b&\approx 1.1447 \qquad \text{Round to 4 decimal places} \end{align*}\]
Unless otherwise stated, do not round any intermediate calculations. Then round the final answer to four places for the remainder of this section.
The exponential model for the population of deer is \(N(t)=80{(1.1447)}^t\). (Note that this exponential function models short-term growth. As the inputs gets large, the output will get increasingly larger, so much so that the model may not be useful in the long term.)
We can graph our model to observe the population growth of deer in the refuge over time. Notice that the graph in Figure \(\PageIndex{3}\) passes through the initial points given in the problem, \((0, 80)\) and \((6, 180)\). We can also see that the domain for the function is \([0,\infty)\),and the range for the function is \([80,\infty)\).
A wolf population is growing exponentially. In 2011, \(129\) wolves were counted. By 2013, the population had reached \(236\) wolves. What two points can be used to derive an exponential equation modeling this situation? Write the equation representing the population \(N\) of wolves over time \(t\).
- Answer
-
\((0,129)\) and \((2,236)\); \(N(t)=129{(1.3526)}^t\)
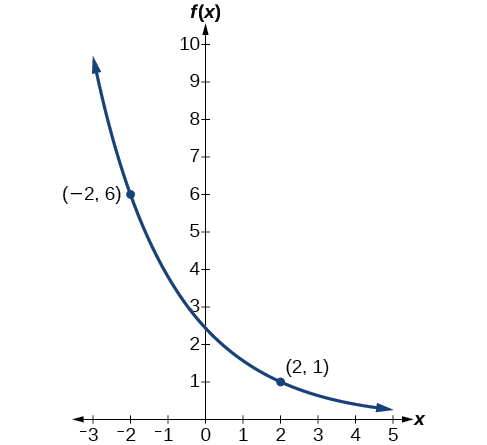
Find an exponential function that passes through the points \((−2,6)\) and \((2,1)\).
Solution
Because we don’t have the initial value, we substitute both points into an equation of the form \(f(x)=ab^x\), and then solve the system for \(a\) and \(b\).
- Substituting \((−2,6)\) gives \(6=ab^{−2}\)
- Substituting \((2,1)\) gives \(1=ab^2\)
Use the first equation to solve for \(a\) in terms of \(b\):
\[\begin{align*} 6&= ab^{-2}\\ \dfrac{6}{b^{-2}}&= a \qquad \text{Divide}\\ a&= 6b^2 \qquad \text{Use properties of exponents to rewrite the denominator} \end{align*}\]
Substitute a in the second equation, and solve for \(b\):
\[\begin{align*} 1&= ab^{2}\\ 1&= 6b^2 b^2\\ &= 6b^4 \qquad \text{Substitute a}\\ b&= \left (\dfrac{1}{6} \right )^{\tfrac{1}{4}} \qquad \text{Round 4 decimal places rewrite the denominator}\\ b&\approx 0.6389 \end{align*}\]
Use the value of \(b\) in the first equation to solve for the value of \(a\):
\[\begin{align*} a&= 6b^{2}\\ &\approx 6(0.6389)^2 \\ &\approx 2.4492 \end{align*}\]
Thus, the equation is \(f(x)=2.4492{(0.6389)}^x\).
We can graph our model to check our work. Notice that the graph in Figure \(\PageIndex{4}\) passes through the initial points given in the problem, \((−2, 6)\) and \((2, 1)\). The graph is an example of an exponential decay function.
Given the two points \((1,3)\) and \((2,4.5)\),find the equation of the exponential function that passes through these two points.
- Answer
-
\(f(x)=2{(1.5)}^x\)
Yes, provided the two points are either both above the x-axis or both below the x-axis and have different x-coordinates. But keep in mind that we also need to know that the graph is, in fact, an exponential function. Not every graph that looks exponential really is exponential. We need to know the graph is based on a model that shows the same percent growth with each unit increase in \(x\), which in many real world cases involves time.
- First, identify two points on the graph. Choose the \(y\)-intercept as one of the two points whenever possible. Try to choose points that are as far apart as possible to reduce round-off error.
- If one of the data points is the \(y\)-intercept \((0,a)\), then \(a\) is the initial value. Using \(a\), substitute the second point into the equation \(f(x)=a{(b)}^x\), and solve for \(b\)
- If neither of the data points have the form \((0,a)\), substitute both points into two equations with the form \(f(x)=a{(b)}^x\). Solve the resulting system of two equations in two unknowns to find \(a\) and \(b\).
- Write the exponential function, \(f(x)=a{(b)}^x\).
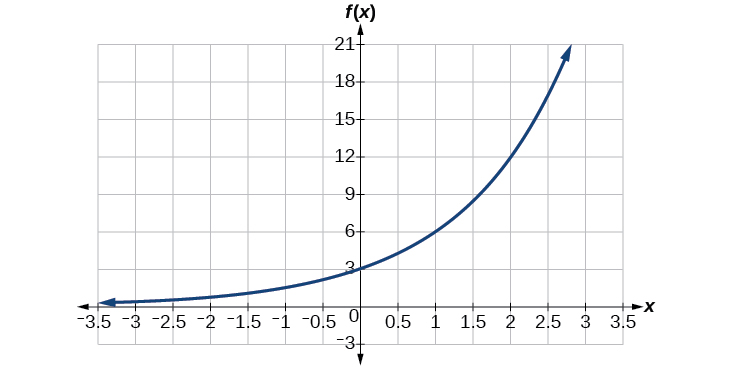
Find an equation for the exponential function graphed in Figure \(\PageIndex{5}\).
Solution
We can choose the \(y\)-intercept of the graph, \((0,3)\), as our first point. This gives us the initial value, \(a=3\). Next, choose a point on the curve some distance away from \((0,3)\) that has integer coordinates. One such point is \((2,12)\).
\[\begin{align*} y&= ab^x \qquad \text{Write the general form of an exponential equation}\\ y&= 3b^x \qquad \text{Substitute the initial value } 3 \text{ for } a\\ 12&= 3b^2 \qquad \text{Substitute in 12 for } y \text{ and } 2 \text{ for } x\\ 4&= b^2 \qquad \text{Divide by }3\\ b&= \pm 2 \qquad \text{Take the square root} \end{align*}\]
Because we restrict ourselves to positive values of \(b\), we will use \(b=2\). Substitute \(a\) and \(b\) into the standard form to yield the equation \(f(x)=3{(2)}^x\).
Find an equation for the exponential function graphed in Figure \(\PageIndex{6}\).
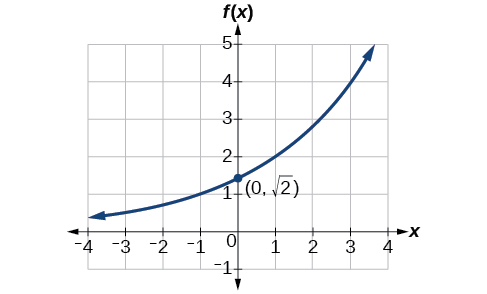
- Answer
-
\(f(x)=\sqrt{2}{(\sqrt{2})}^x\). Answers may vary due to round-off error. The answer should be very close to \(1.4142{(1.4142)}^x\).
- Press [STAT].
- Clear any existing entries in columns L1 or L2.
- In L1, enter the x-coordinates given.
- In L2, enter the corresponding y-coordinates.
- Press [STAT] again. Cursor right to CALC, scroll down to ExpReg (Exponential Regression), and press [ENTER].
- The screen displays the values of a and b in the exponential equation \(y=a⋅b^x\).
Use a graphing calculator to find the exponential equation that includes the points \((2,24.8)\) and \((5,198.4)\).
Solution
Follow the guidelines above. First press [STAT], [EDIT], [1: Edit…], and clear the lists L1 and L2. Next, in the L1 column, enter the \(x\)-coordinates, \(2\) and \(5\). Do the same in the L2 column for the \(y\)-coordinates, \(24.8\) and \(198.4\).
Now press [STAT], [CALC], [0: ExpReg] and press [ENTER]. The values \(a=6.2\) and \(b=2\) will be displayed. The exponential equation is \(y=6.2⋅2^x\).
Use a graphing calculator to find the exponential equation that includes the points \((3, 75.98)\) and \((6, 481.07)\).
- Answer
-
\(y≈12⋅{1.85}^x\)
Applying the Compound-Interest Formula
Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, use compound interest. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.
The annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account. The term nominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than once a year, the effective interest rate ends up being greater than the nominal rate! This is a powerful tool for investing.
We can calculate the compound interest using the compound interest formula, which is an exponential function of the variables time \(t\), principal \(P\), \(APR\) \(r\), and number of compounding periods in a year \(n\):
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt} \nonumber\]
For example, observe Table \(\PageIndex{4}\), which shows the result of investing \($1,000\) at \(10\%\) for one year. Notice how the value of the account increases as the compounding frequency increases.
| Frequency | Value after \(1\) year |
|---|---|
| Annually | \($1100\) |
| Semiannually | \($1102.50\) |
| Quarterly | \($1103.81\) |
| Monthly | \($1104.71\) |
| Daily | \($1105.16\) |
Compound interest can be calculated using the formula
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt}\]
where
- \(A(t)\) is the account value,
- \(t\) is measured in years,
- \(P\) is the starting amount of the account, often called the principal, or more generally present value,
- \(r\) is the annual percentage rate (APR) expressed as a decimal, and
- \(n\) is the number of compounding periods in one year.
If we invest \($3,000\) in an investment account paying \(3\%\) interest compounded quarterly, how much will the account be worth in \(10\) years?
Solution
Because we are starting with \($3,000\), \(P=3000\). Our interest rate is \(3\%\), so \(r = 0.03\). Because we are compounding quarterly, we are compounding \(4\) times per year, so \(n=4\). We want to know the value of the account in \(10\) years, so we are looking for \(A(10)\),the value when \(t = 10\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ A(10)&= 3000{\left (1+\dfrac{0.03}{4} \right )}^{(4)\cdot (10)} \qquad \text{Substitute using given values}\\ &\approx \$4045.05 \qquad \text{Round to two decimal places} \end{align*}\]
The account will be worth about \($4,045.05\) in \(10\) years.
An initial investment of \($100,000\) at \(12\%\) interest is compounded weekly (use \(52\) weeks in a year). What will the investment be worth in \(30\) years?
- Answer
-
about \($3,644,675.88\)
A 529 Plan is a college-savings plan that allows relatives to invest money to pay for a child’s future college tuition; the account grows tax-free. Lily wants to set up a 529 account for her new granddaughter and wants the account to grow to \($40,000\) over \(18\) years. She believes the account will earn \(6\%\) compounded semi-annually (twice a year). To the nearest dollar, how much will Lily need to invest in the account now?
Solution
The nominal interest rate is \(6\%\), so \(r=0.06\). Interest is compounded twice a year, so \(k=2\).
We want to find the initial investment, \(P\), needed so that the value of the account will be worth \($40,000\) in \(18\) years. Substitute the given values into the compound interest formula, and solve for \(P\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ 40,000&= P{\left (1+\dfrac{0.06}{2} \right )}^{2(18)} \qquad \text{Substitute using given values } A, r, n, t\\ 40,000&= P{(1.03)}^{36} \qquad \text{Simplify}\\ \dfrac{40,000}{ {(1.03)}^{36} }&= P \qquad \text{Isolate } P\\ P&\approx \$13,801 \qquad \text{Divide and round to the nearest dollar} \end{align*}\]
Lily will need to invest \($13,801\) to have \($40,000\) in \(18\) years.
Refer to Example \(\PageIndex{9}\). To the nearest dollar, how much would Lily need to invest if the account is compounded quarterly?
- Answer
-
\($13,693\)
Evaluating Functions with Base \(e\)
As we saw earlier, the amount earned on an account increases as the compounding frequency increases. Table \(\PageIndex{5}\) shows that the increase from annual to semi-annual compounding is larger than the increase from monthly to daily compounding. This might lead us to ask whether this pattern will continue.
Examine the value of \($1\) invested at \(100\%\) interest for \(1\) year, compounded at various frequencies, listed in Table \(\PageIndex{5}\).
| Frequency | \(A(t)={\left (1+\dfrac{1}{n} \right )}^n\) | Value |
|---|---|---|
| Annually | \({\left (1+\dfrac{1}{1} \right )}^1\) | \($2\) |
| Semiannually | \({\left (1+\dfrac{1}{2} \right )}^2\) | \($2.25\) |
| Quarterly | \({\left (1+\dfrac{1}{4} \right )}^4\) | \($2.441406\) |
| Monthly | \({\left (1+\dfrac{1}{12} \right )}^{12}\) | \($2.613035\) |
| Daily | \({\left (1+\dfrac{1}{365} \right )}^{365}\) | \($2.714567\) |
| Hourly | \({\left (1+\dfrac{1}{8760} \right )}^{8760}\) | \($2.718127\) |
| Once per minute | \({\left (1+\dfrac{1}{525600} \right )}^{525600}\) | \($2.718279\) |
| Once per second | \({\left (1+\dfrac{1}{31536000} \right )}^{31536000}\) | \($2.718282\) |
These values appear to be approaching a limit as \(n\) increases without bound. In fact, as \(n\) gets larger and larger, the expression \({\left (1+\dfrac{1}{n} \right )}^n\) approaches a number used so frequently in mathematics that it has its own name: the letter \(e\). This value is an irrational number, which means that its decimal expansion goes on forever without repeating. Its approximation to six decimal places is shown below.
The letter \(e\) represents the irrational number
\[{\left (1+\dfrac{1}{n} \right )}^n\]
as \(n\) increases without bound
The letter \(e\) is used as a base for many real-world exponential models. To work with base \(e\), we use the approximation, \(e≈2.718282\). The constant was named by the Swiss mathematician Leonhard Euler (1707–1783) who first investigated and discovered many of its properties.
Calculate \(e^{3.14}\). Round to five decimal places.
Solution
On a calculator, press the button labeled \([e^x]\). The window shows \([e {}^( ]\). Type \(3.14\) and then close parenthesis, \([)]\). Press [ENTER]. Rounding to \(5\) decimal places, \(e^{3.14}≈23.10387\). Caution: Many scientific calculators have an “Exp” button, which is used to enter numbers in scientific notation. It is not used to find powers of \(e\).
Use a calculator to find \(e^{−0.5}\). Round to five decimal places.
- Answer
-
\(e^{−0.5}≈0.60653\)
Investigating Continuous Growth
So far we have worked with rational bases for exponential functions. For most real-world phenomena, however, \(e\) is used as the base for exponential functions. Exponential models that use \(e\) as the base are called continuous growth or decay models. We see these models in finance, computer science, and most of the sciences, such as physics, toxicology, and fluid dynamics.
For all real numbers \(t\),and all positive numbers \(a\) and \(r\), continuous growth or decay is represented by the formula
\[A(t)=ae^{rt}\]
where
- \(a\) is the initial value,
- \(r\) is the continuous growth rate per unit time,
- \(t\) is the elapsed time.
If \(r>0\), then the formula represents continuous growth. If \(r<0\), then the formula represents continuous decay.
For business applications, the continuous growth formula is called the continuous compounding formula and takes the form
\[A(t)=Pe^{rt}\]
where
- \(P\) is the principal or the initial invested,
- \(r\) is the growth or interest rate per unit time,
- \(t\) is the period or term of the investment.
- Use the information in the problem to determine \(a\), the initial value of the function.
- Use the information in the problem to determine the growth rate \(r\).
- If the problem refers to continuous growth, then \(r>0\).
- If the problem refers to continuous decay, then \(r<0\).
- Use the information in the problem to determine the time \(t\).
- Substitute the given information into the continuous growth formula and solve for \(A(t)\).
A person invested \($1,000\) in an account earning a nominal \(10\%\) per year compounded continuously. How much was in the account at the end of one year?
Solution
Since the account is growing in value, this is a continuous compounding problem with growth rate \(r=0.10\). The initial investment was \($1,000\), so \(P=1000\). We use the continuous compounding formula to find the value after \(t=1\) year:
\[\begin{align*} A(t)&= Pe^{rt} \qquad \text{Use the continuous compounding formula}\\ &= 1000{(e)}^{0.1} \qquad \text{Substitute known values for } P, r, t\\ &\approx 1105.17 \qquad \text{Use a calculator to approximate} \end{align*}\]
The account is worth \($1,105.17\) after one year.
A person invests \($100,000\) at a nominal \(12\%\) interest per year compounded continuously. What will be the value of the investment in \(30\) years?
- Answer
-
\($3,659,823.44\)
\(Radon-222\) decays at a continuous rate of \(17.3\%\) per day. How much will \(100 mg\) of \(Radon-222\) decay to in \(3\) days?
Solution
Since the substance is decaying, the rate, \(17.3\%\), is negative. So, \(r = −0.173\). The initial amount of \(Radon-222\) was \(100\) mg, so \(a=100\). We use the continuous decay formula to find the value after \(t=3\) days:
\[\begin{align*} A(t)&= ae^{rt} \qquad \text{Use the continuous growth formula}\\ &= 100e6{-0.173(3)} \qquad \text{Substitute known values for } a, r, t\\ &\approx 59.5115 \qquad \text{Use a calculator to approximate} \end{align*}\]
So \(59.5115\) mg of \(Radon-222\) will remain.
Using the data in Example \(\PageIndex{12}\), how much \(Radon-222\) will remain after one year?
- Answer
-
\(3.77E-26\) (This is calculator notation for the number written as \(3.77×10^{−26}\) in scientific notation. While the output of an exponential function is never zero, this number is so close to zero that for all practical purposes we can accept zero as the answer.)
Access these online resources for additional instruction and practice with exponential functions.
- Exponential Growth Function
- Compound Interest
Key Equations
| definition of the exponential function | \(f(x)=b^x\), where \(b>0\), \(b≠1\) |
| definition of exponential growth | \(f(x)=ab^x\), where \(a>0\), \(b>0\), \(b≠1\) |
| compound interest formula |
\(A(t)=P{(1+\dfrac{r}{n})}^{nt}\), where \(A(t)\) is the account value at time \(t\) \(t\) is the number of years \(P\) is the initial investment, often called the principal \(r\) is the annual percentage rate (APR), or nominal rate \(n\) is the number of compounding periods in one year |
| continuous growth formula | \(A(t)=ae^{rt}\), where \(t\) is the number of unit time periods of growth \(a\) is the starting amount (in the continuous compounding formula a is replaced with \(P\), the principal) \(e\) is the mathematical constant, \(e≈2.718282\) |
Key Concepts
- An exponential function is defined as a function with a positive constant other than \(1\) raised to a variable exponent. See Example.
- A function is evaluated by solving at a specific value. See Example and Example.
- An exponential model can be found when the growth rate and initial value are known. See Example.
- An exponential model can be found when the two data points from the model are known. See Example.
- An exponential model can be found using two data points from the graph of the model. See Example.
- An exponential model can be found using two data points from the graph and a calculator. See Example.
- The value of an account at any time \(t\) can be calculated using the compound interest formula when the principal, annual interest rate, and compounding periods are known. See Example.
- The initial investment of an account can be found using the compound interest formula when the value of the account, annual interest rate, compounding periods, and life span of the account are known. See Example.
- The number \(e\) is a mathematical constant often used as the base of real world exponential growth and decay models. Its decimal approximation is \(e≈2.718282\).
- Scientific and graphing calculators have the key \([ex]\) or \([exp(x)]\) for calculating powers of \(e\). See Example.
- Continuous growth or decay models are exponential models that use \(e\) as the base. Continuous growth and decay models can be found when the initial value and growth or decay rate are known. See Example and Example.


