7.2: Series Solutions of Linear Second Order ODEs
- Page ID
- 358
Suppose we have a linear second order homogeneous ODE of the form
\[ p(x)y'' + q(x)y' + r(x)y = 0 \label{eq1} \]
Suppose that \(p(x)\), \(q(x)\), and \(r(x)\) are polynomials. We will try a solution of the form
\[ y = \sum_{k=0}^\infty a_k\left(x-x_o\right)^2 \nonumber \]
and solve for the \(a_k\) to try to obtain a solution defined in some interval around \(x_o\).
The point \(x_o\) is called an ordinary point if \(p(x_o) \neq 0\) in linear second order homogeneous ODE of the form in Equation \ref{eq1}. That is, the functions
\[ \dfrac{q(x)}{p(x)} \quad\text{and}\quad \dfrac{r(x)}{p(x)} \nonumber \]
are defined for \(x\) near \(x_o\).
If \( p(x_0)=0\), then we say \(x_o\) is a singular point.
Handling singular points is harder than ordinary points and so we now focus only on ordinary points.
Let us start with a very simple example
\[ y'' - y = 0 \nonumber \]
Let us try a power series solution near \(x_o=0\), which is an ordinary point.
Solution
Every point is an ordinary point in fact, as the equation is constant coefficient. We already know we should obtain exponentials or the hyperbolic sine and cosine, but let us pretend we do not know this.
We try
\[ y = \sum_{k=0}^\infty a_k x^k \nonumber \]
If we differentiate, the \( k=0 \) term is a constant and hence disappears. We therefore get
\[ y' = \sum_{k=1}^\infty k\, a_k \, x^{k-1} \nonumber \]
We differentiate yet again to obtain (now the \(k=1\) term disappears)
\[ y'' = \sum_{k=2}^\infty k\, (k-1)\, a_k \, x^{k-2} \nonumber \]
We reindex the series (replace \(k\) with \( k+2 \) ) to obtain
\[ y'' = \sum_{k=0}^\infty (k+2)\, (k+1)\, a_{k+2} \, x^k \nonumber \]
Now we plug \(y\) and \(y''\) into the differential equation.
\[\begin{align}\begin{aligned} 0 = y''-y &= \Biggl( \sum_{k=0}^\infty (k+2)(k+1) a_{k+2} x^k \Biggr) - \Biggl( \sum_{k=0}^\infty a_k x^k \Biggr) \\ &= \sum_{k=0}^\infty \Bigl( (k+2) (k+1) a_{k+2} x^k - a_k x^k \Bigr) \\ &= \sum_{k=0}^\infty \bigl( (k+2)(k+1) a_{k+2} - a_k \bigr) x^k .\end{aligned}\end{align} \nonumber \]
As \( y''-y\) is supposed to be equal to 0, we know that the coefficients of the resulting series must be equal to 0. Therefore,
\[ (k+2) (k+1) a_{k+2} - a_k = 0 , \qquad \text{or} \qquad a_{k+2} = \dfrac{a_k}{(k+2)(k+1)} . \nonumber \]
The above equation is called a recurrence relation for the coefficients of the power series. It did not matter what \(a_0\) or \(a_1\) was. They can be arbitrary. But once we pick \(a_0\) and \(a_1\), then all other coefficients are determined by the recurrence relation.
Let us see what the coefficients must be. First, \(a_0\) and \(a_1\) are arbitrary
\[ a_2 = \dfrac{a_0}{2}, \quad a_3 = \dfrac{a_1}{(3)(2)}, \quad a_4 = \dfrac{a_2}{(4)(3)} = \dfrac{a_0}{(4)(3)(2)}, \quad a_5 = \dfrac{a_3}{(5)(4)} = \dfrac{a_1}{(5)(4)(3)(2)}, \quad \ldots \nonumber \]
So we note that for even \(k\), that is \( k=2n\) we get
\[ a_k = a_{2n} = \dfrac{a_o}{(2n)!} \nonumber \]
and for odd \(k\) that is \( k=2n+1\) we have
\[ a_k = a_{2n+1} = \dfrac{a_1}{(2n+1)!} \nonumber \]
Let us write down the series
\[y =\sum_{k=0}^\infty a_k x^k= \sum_{n=0}^\infty \left( \dfrac{a_0}{(2n)!} \,x^{2n} +\dfrac{a_1}{(2n+1)!} \,x^{2n+1} \right) =a_0 \sum_{n=0}^\infty \dfrac{1}{(2n)!} \,x^{2n}+a_1 \sum_{n=0}^\infty \dfrac{1}{(2n+1)!} \,x^{2n+1} . \nonumber \]
We recognize the two series as the hyperbolic sine and cosine. Therefore,
\[ y= a_o \, \text{cosh} \, x + a_1\, \text{sinh}\, x \nonumber \]
Of course, in general we will not be able to recognize the series that appears, since usually there will not be any elementary function that matches it. In that case we will be content with the series.
Let us do a more complex example. Suppose we wish to solve Airy’s equation\(^{1}\), that is
\[ y'' - xy = 0 \nonumber \]
near the point \( x_0 = 0 \), which is an ordinary point.
We try
\[ y = \sum_{k=0}^{\infty} a_k x^k \nonumber \]
We differentiate twice (as above) to obtain
\[ y'' = \sum_{k=2}^{\infty} k(k-1)a_k x^{k-2} \nonumber \]
We plug \(y\) into the equation
\[\begin{align}\begin{aligned} 0 = y''-xy &= \Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr)-x \Biggl( \sum_{k=0}^\infty a_k x^k \Biggr) \\ &= \Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr)-\Biggl( \sum_{k=0}^\infty a_k x^{k+1} \Biggr) .\end{aligned}\end{align} \nonumber \]
We reindex to make things easier to sum
\[\begin{align}\begin{aligned} 0 = y''-xy &= \Biggl( 2 a_2 + \sum_{k=1}^\infty (k+2)\,(k+1) \, a_{k+2} x^k \Biggr) - \Biggl( \sum_{k=1}^\infty a_{k-1} x^k \Biggr) . \\ &= 2 a_2 + \sum_{k=1}^\infty \Bigl( (k+2)\,(k+1) \, a_{k+2} - a_{k-1} \Bigr) \, x^k .\end{aligned}\end{align} \nonumber \]
Again \( y'' - xy\) is supposed to be 0 so first we notice that \(a_2 = 0 \) and also
\[ (k+2)\,(k+1) \,a_{k+2} - a_{k-1} = 0 , \qquad \text{or} \qquad a_{k+2} = \dfrac{a_{k-1}}{(k+2)(k+1)} . \nonumber \]
Now we jump in steps of three. First we notice that since \(a_2 = 0\) we must have that, \(a_5 = 0\), \(a_8 = 0\), \(a_{11}=0\), etc \(\ldots\). In general \(a_{3n+2} =0\). The constants \(a_0\) and \(a_1\) are arbitrary and we obtain
\[a_3 = \dfrac{a_0}{(3)(2)}, \quad a_4 = \dfrac{a_1}{(4)(3)}, \quad a_6 = \dfrac{a_3}{(6)(5)} = \dfrac{a_0}{(6)(5)(3)(2)}, \quad a_7 = \dfrac{a_4}{(7)(6)} = \dfrac{a_1}{(7)(6)(4)(3)}, \quad \ldots \nonumber \]
For \(a_k\) where \(k\) is a multiple of \(3\), that is \(k=3n\) we notice that
\[a_{3n} = \dfrac{a_0}{(2)(3)(5)(6) \cdots (3n-1)(3n)} . \nonumber \]
For \(a_k\) where \(k = 3n+1\), we notice
\[a_{3n+1} = \dfrac{a_1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} . \nonumber \]
In other words, if we write down the series for \(y\) we notice that it has two parts
\[\begin{align}\begin{aligned} y &=\left( a_0 + \dfrac{a_0}{6} x^3 + \dfrac{a_0}{180} x^6 + \cdots + \dfrac{a_0}{(2)(3)(5)(6) \cdots (3n-1)(3n)} x^{3n} + \cdots \right) \\ & \phantom{=}+\left( a_1 x + \dfrac{a_1}{12} x^4 + \dfrac{a_1}{504} x^7 + \cdots + \dfrac{a_1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} x^{3n+1} + \cdots \right) \\ &=a_0 \left(1 + \dfrac{1}{6} x^3 + \dfrac{1}{180} x^6 + \cdots + \dfrac{1}{(2)(3)(5)(6) \cdots (3n-1)(3n)} x^{3n} + \cdots \right) \\ &\phantom{=}+a_1\left(x + \dfrac{1}{12} x^4 + \dfrac{1}{504} x^7 + \cdots +\dfrac{1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} x^{3n+1} + \cdots \right) .\end{aligned}\end{align} \nonumber \]
We define
\[\begin{align}\begin{aligned} y_1(x) &= 1 + \dfrac{1}{6} x^3 + \dfrac{1}{180} x^6 + \cdots + \dfrac{1}{(2)(3)(5)(6) \cdots (3n-1)(3n)} x^{3n} + \cdots, \\y_2(x) &= x + \dfrac{1}{12} x^4 + \dfrac{1}{504} x^7 + \cdots + \dfrac{1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} x^{3n+1} + \cdots ,\end{aligned}\end{align} \nonumber \]
and write the general solution to the equation as \(y(x)= a_0 y_1(x) + a_1 y_2(x)\). Notice from the power series that \(y_1(0) = 1\) and \(y_2(0) = 0\). Also, \(y_1'(0) = 0\) and \(y_2'(0) = 1\). Therefore \(y(x)\) is a solution that satisfies the initial conditions \(y(0) = a_0\) and \(y'(0) = a_1\).
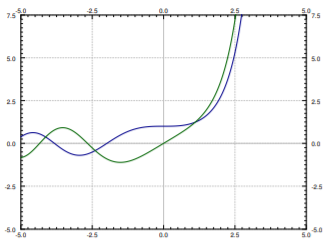
The functions \(y_1\) and \(y_2\) cannot be written in terms of the elementary functions that you know. See Figure \(\PageIndex{1}\) for the plot of the solutions \(y_1\) and \(y_2\). These functions have many interesting properties. For example, they are oscillatory for negative \(x\) (like solutions to \(y''+y=0\)) and for positive \(x\) they grow without bound (like solutions to \(y''-y=0\)).
Sometimes a solution may turn out to be a polynomial.
Let us find a solution to the so-called Hermite’s equation of order \(n\)\(^{2}\) is the equation
\[ y'' -2xy' + 2n y = 0 . \nonumber \]
Find a solution around the point \(x_0 = 0\).
Solution
We try
\[y = \sum_{k=0}^\infty a_k x^k . \nonumber \]
We differentiate (as above) to obtain
\[\begin{align}\begin{aligned} y' =& \sum_{k=1}^\infty k a_k x^{k-1} , \\ y'' &= \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} .\end{aligned}\end{align} \nonumber \]
Now we plug into the equation
\[\begin{align}\begin{aligned} 0 &= y''-2xy'+2ny \\ &= \Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr) -2x \Biggl( \sum_{k=1}^\infty k a_k x^{k-1} \Biggr)+2n \Biggl( \sum_{k=0}^\infty a_k x^k \Biggr) \\ &=\Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr)- \Biggl( \sum_{k=1}^\infty 2k a_k x^k \Biggr) + \Biggl( \sum_{k=0}^\infty 2n a_k x^k \Biggr) \\ &= \Biggl(2a_2+ \sum_{k=1}^\infty (k+2)\,(k+1) \, a_{k+2} x^k \Biggr) - \Biggl( \sum_{k=1}^\infty 2k a_k x^k \Biggr) + \Biggl( 2na_0 + \sum_{k=1}^\infty 2n a_k x^k \Biggr) \\ &=2a_2+2na_0+ \sum_{k=1}^\infty \bigl( (k+2)\,(k+1) \, a_{k+2} - 2ka_k + 2n a_k \bigr) x^k .\end{aligned}\end{align} \nonumber \]
As \(y''-2xy'+2ny = 0\) we have
\[(k+2)\,(k+1) \, a_{k+2} + ( - 2k+ 2n) a_k = 0 , \qquad \text{or} \qquad a_{k+2} = \dfrac{(2k-2n)}{(k+2)(k+1)} a_k . \nonumber \]
This recurrence relation actually includes \(a_2 = -na_0\) (which comes about from \(2a_2+2na_0 = 0\)). Again \(a_0\) and \(a_1\) are arbitrary.
\[\begin{align}\begin{aligned} a_2 &= \dfrac{-2n}{(2)(1)}a_0, \qquad a_3 = \dfrac{2(1-n)}{(3)(2)} a_1, \\ a_4& = \dfrac{2(2-n)}{(4)(3)} a_2 = \dfrac{2^2(2-n)(-n)}{(4)(3)(2)(1)} a_0 , \\ a_5& = \dfrac{2(3-n)}{(5)(4)} a_3 = \dfrac{2^2(3-n)(1-n)}{(5)(4)(3)(2)} a_1 , \quad \ldots\end{aligned}\end{align} \nonumber \]
Let us separate the even and odd coefficients. We find that
\[\begin{align}\begin{aligned} a_{2m} &=\dfrac{2^m(-n)(2-n)\cdots(2m-2-n)}{(2m)!} , \\ a_{2m+1} &=\dfrac{2^m(1-n)(3-n)\cdots(2m-1-n)}{(2m+1)!} .\end{aligned}\end{align} \nonumber \]
Let us write down the two series, one with the even powers and one with the odd.
\[\begin{align}\begin{aligned} y_1(x) &= 1+\dfrac{2(-n)}{2!} x^2 + \dfrac{2^2(-n)(2-n)}{4!} x^4 + \dfrac{2^3(-n)(2-n)(4-n)}{6!} x^6 + \cdots , \\ y_2(x) &= x+\dfrac{2(1-n)}{3!} x^3 + \dfrac{2^2(1-n)(3-n)}{5!} x^5 + \dfrac{2^3(1-n)(3-n)(5-n)}{7!} x^7 + \cdots .\end{aligned}\end{align} \nonumber \]
We then write
\[y(x) = a_0 y_1(x) + a_1 y_2(x) . \nonumber \]
We also notice that if \(n\) is a positive even integer, then \(y_1(x)\) is a polynomial as all the coefficients in the series beyond a certain degree are zero. If \(n\) is a positive odd integer, then \(y_2(x)\) is a polynomial. For example, if \(n=4\), then
\[ y_1(x) = 1 + \dfrac{2(-4)}{2!} x^2 + \dfrac{2^2(-4)(2-4)}{4!} x^4= 1 - 4x^2 + \dfrac{4}{3} x^4 . \nonumber \]
Footnotes
[1] Named after the English mathematician Sir George Biddell Airy (1801 – 1892).
[2] Named after the French mathematician Charles Hermite (1822–1901).


