3.5.1 Appendix: Real Analytic Functions
- Page ID
- 2175
Multi-index notation
The following multi-index notation simplifies many presentations of formulas. Let \(x=(x_1,\ldots,x_n)\) and
$$
u:\ \Omega\subset\mathbb{R}\mapsto \mathbb{R}^1\ \ (\mbox{or}\ \mathbb{R}^m\ \mbox{for systems}).
$$
The n-tuple of non-negative integers (including zero)
$$
\alpha=(\alpha_1,\ldots,\alpha_n)
$$
is called multi-index. Set
\begin{eqnarray*}
|\alpha|&=&\alpha_1+\ldots+\alpha_n\\
\alpha!&=&\alpha_1!\alpha_2!\cdot\ldots\cdot\alpha_n!\\
x^\alpha&=&x_1^{\alpha_1}x_2^{\alpha_2}\cdot\ldots\cdot x_n^{\alpha_n}\ \ (\mbox{for a monom})\\
D_k&=&\frac{\partial}{\partial x_k}\\
D&=&(D_1,\ldots,D_n)\\
Du&=&(D_1u,\ldots,D_nu)\equiv\nabla u\equiv \text{grad}\ u\\
D^\alpha&=&D_1^{\alpha_1}D_2^{\alpha_2}\cdot\ldots\cdot D_n^{\alpha_n}\equiv\frac{\partial^{|\alpha|}}{\partial x_1^{\alpha_1}\partial x_2^{\alpha_2}\ldots\partial x_n^{\alpha_n}}.
\end{eqnarray*}
Define a partial order by
$$
\alpha\ge\beta\ \ \mbox{if and only if}\ \ \alpha_i\ge\beta_i\ \ \mbox{for all}\ i.
$$
Sometimes we use the notations
$$
{\bf 0}=(0,0\ldots,0), \ \ \bf{ 1}=(1,1\ldots,1),
$$
where
\({\bf 0},\ {\bf 1}\in\mathbb{R}.\)
Using this multi-index notion, we have
1.
$$
(x+y)^\alpha=\sum_{\begin{array}{c}\beta,\gamma\\ \beta+\gamma=\alpha\end{array}}\frac{\alpha!}{\beta!\gamma!}x^\beta y^\gamma,
$$
where \(x,\ y\in\mathbb{R}\) and \(\alpha,\ \beta,\ \gamma\) are multi-indices.
2. Taylor expansion for a polynomial \(f(x)\) of degree \(m\):
$$
f(x)=\sum_{|\alpha|\le m}\frac{1}{\alpha!}\left(D^\alpha f(0)\right) x^\alpha,
$$
here is \(D^\alpha f(0):=\left(D^\alpha f(x)\right)|_{x=0}\).
3. Let \(x=(x_1,\ldots,x_n)\) and \(m\ge0\) an integer, then
$$
(x_1+\ldots+x_n)^m=\sum_{|\alpha|=m}\frac{m!}{\alpha!}x^\alpha.
\]
4.
$$
\alpha!\le|\alpha|!\le n^{|\alpha|}\alpha!.
\]
5. Leibniz's rule:
$$
D^\alpha(fg)=
\sum_{\begin{array}{c}\beta,\gamma\\ \beta+\gamma=\alpha\end{array}}\frac{\alpha!}{\beta!\gamma!}(D^\beta f)(D^\gamma g).
\]
6.
\begin{eqnarray*}
D^\beta x^\alpha&=&\frac{\alpha!}{(\alpha-\beta)!}x^{\alpha-\beta}\ \ \mbox{if}\ \alpha\ge\beta,\\
D^\beta x^\alpha&=&0\ \ \mbox{otherwise}.
\end{eqnarray*}
7. Directional derivative:
$$
\frac{d^m}{dt^m}f(x+ty)=\sum_{|\alpha|=m}\frac{|\alpha|!}{\alpha!}\left(D^\alpha f(x+ty)\right)y^\alpha,
$$
where \(x,\ y\in\mathbb{R}\) and \(t\in\mathbb{R}^1\).
8. Taylor's theorem: Let \(u\in C^{m+1}\) in a neighborhood \(N(y)\) of \(y\), then, if \(x\in N(y)\),
$$
u(x)=\sum_{|\alpha|\le m}\frac{1}{\alpha!}\left(D^\alpha u(y)\right)(x-y)^\alpha+R_m,
$$
where
$$
R_m=\sum_{|\alpha|=m+1}\frac{1}{\alpha!}\left(D^\alpha u(y+\delta(x-y))\right)x^\alpha,\ 0<\delta<1,
$$
\(\delta=\delta(u,m,x,y)\),
or
$$
R_m=\frac{1}{m!}\int_0^1\ (1-t)^m\Phi^{(m+1)}(t)\ dt,
$$
where \(\Phi(t)=u(y+t(x-y))\). It follows from 7. that
$$
R_m=(m+1)\sum_{|\alpha|=m+1}\frac{1}{\alpha!}\left(\int_0^1\ (1-t)D^\alpha u(y+t(x-y))\ dt\right)(x-y)^\alpha.
\]
9. Using multi-index notation, the general linear partial differential equation of order \(m\) can be written as
$$
\sum_{|\alpha|\le m}a_\alpha (x)D^\alpha u=f(x)\ \ \mbox{in}\ \Omega\subset\mathbb{R}.
\]
Power series
Here we collect some definitions and results for power series in \(\mathbb{R}\).
Definition. Let \(c_\alpha\in\mathbb{R}^1\ (\mbox{or}\ \in\mathbb{R}^m)\). The series
$$
\sum_\alpha c_\alpha\equiv\sum_{m=0}^\infty\left(\sum_{|\alpha|=m}c_\alpha\right)
$$
is said to be convergent if
$$
\sum_\alpha |c_\alpha|\equiv\sum_{m=0}^\infty\left(\sum_{|\alpha|=m}|c_\alpha|\right)
$$
is convergent.
Remark. According to the above definition, a convergent series is absolutely convergent. It follows that we can rearrange the order of summation.
Using the above multi-index notation and keeping in mind that we can rearrange convergent series, we have
10. Let \(x\in\mathbb{R}\), then
\begin{eqnarray*}
\sum_\alpha x^\alpha&=&\prod_{i=1}^n\left(\sum_{\alpha_i=0}^\infty x_i^{\alpha_i}\right)\\
&=&\frac{1}{(1-x_1)(1-x_2)\cdot\ldots\cdot(1-x_n)}\\
&=&\frac{1}{({\bf 1}-x)^{\bf 1}},
\end{eqnarray*}
provided \(|x_i|<1\) is satisfied for each \(i\).
11. Assume \(x\in\mathbb{R}\) and \(|x_1|+|x_2|+\ldots+|x_n|<1\), then
\begin{eqnarray*}
\sum_\alpha\frac{|\alpha|!}{\alpha!}x^\alpha&=&\sum_{j=0}^\infty\sum_{|\alpha|=j}\frac{|\alpha|!}{\alpha!}x^\alpha\\
&=&\sum_{j=0}^\infty(x_1+\ldots+x_n)^j\\
&=&\frac{1}{1-(x_1+\ldots+x_n)}.
\end{eqnarray*}
12. Let \(x\in\mathbb{R}\), \(|x_i|<1\) for all \(i\), and \(\beta\) is a given multi-index. Then
\begin{eqnarray*}
\sum_{\alpha\ge\beta}\frac{\alpha!}{(\alpha-\beta)!}x^{\alpha-\beta}&=&D^\beta\frac{1}{({\bf 1}-x)^1}\\
&=&\frac{\beta!}{({\bf 1}-x)^{1+\beta}}\
\end{eqnarray*}
13. Let \(x\in\mathbb{R}\) and \(|x_1|+\ldots+|x_n|<1\). Then
\begin{eqnarray*}
\sum_{\alpha\ge\beta}\frac{|\alpha|!}{(\alpha-\beta)!}x^{\alpha-\beta}&=&D^\beta\frac{1}{1-x_1-\ldots-x_n}\\
&=&\frac{|\beta|!}{(1-x_1-\ldots-x_n)^{1+|\beta|}}\ .
\end{eqnarray*}
Consider the power series
\begin{equation}
\label{power}\tag{3.34}
\sum_\alpha c_\alpha x^\alpha
\end{equation}
and assume this series is convergent for a \(z\in\mathbb{R}\). Then, by definition,
$$
\mu:=\sum_\alpha|c_\alpha||z^\alpha|<\infty
$$
and the series (\ref{power}) is uniformly convergent for all \(x\in Q(z)\), where
$$
Q(z):\ \ |x_i|\le|z_i|\ \ \mbox{for all}\ \ i.
\]
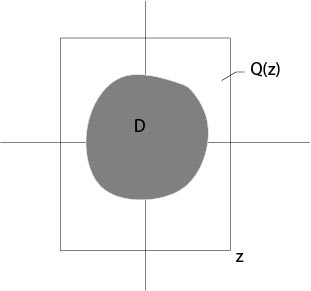
Figure 3.5.1.1: Definition of \(D\in Q(z)\)
Thus the power series (\ref{power}) defines a continuous function defined on \(Q(z)\), according to a theorem of Weierstrass.
The interior of \(Q(z)\) is not empty if and only if \(z_i\not=0\) for all \(i\), see Figure 3.5.1.1.
For given \(x\) in a fixed compact subset \(D\) of \(Q(z)\) there is a \(q\), \(0<q<1\), such that
$$
|x_i|\le q|z_i|\ \ \mbox{for all}\ i.
$$
Set
$$
f(x)=\sum_\alpha c_\alpha x^\alpha.
\]
Proposition A1. (i) In every compact subset \(D\) of \(Q(z)\) one has \(f\in C^\infty(D)\) and
the formal differentiate series, that is \(\sum_\alpha D^\beta c_\alpha x^\alpha\), is uniformly convergent on the closure of \(D\) and is equal to \(D^\beta f\).}
(ii)
$$
|D^\beta f(x)|\le M|\beta|!r^{-|\beta|}\ \ \mbox{in}\ D,
$$
where
$$
M=\frac{\mu}{(1-q)^n},\qquad \qquad r=(1-q)\min_i|z_i|.
$$
Proof. See F. John [10], p. 64. Or an exercise. Hint: Use formula 12. where \(x\) is replaced by \((q,\ldots,q)\).
Remark. From the proposition above it follows
$$
c_\alpha=\frac{1}{\alpha!}D^\alpha f(0).
\]
Definition. Assume \(f\) is defined on a domain \(\Omega\subset\mathbb{R}\), then \(f\) is said to be {\it real analytic in \(y\in\Omega\)} if there are \(c_\alpha\in\mathbb{R}^1\) and if there is a neighborhood \(N(y)\) of \(y\) such that
$$
f(x)=\sum_\alpha c_\alpha(x-y)^\alpha
$$
for all \(x\in N(y)\), and the series converges (absolutely) for each \(x\in N(y)\).
A function \(f\) is called {\it real analytic in \(\Omega\)} if it is real analytic for each \(y\in\Omega\).
We will write \(f\in C^\omega(\Omega)\) in the case that \(f\) is real analytic in the domain \(\Omega\).
A vector valued function \(f(x)=(f_1(x),\ldots,f_m)\) is called real analytic if each coordinate is real analytic.
Proposition A2. (i) Let \(f\in C^\omega(\Omega)\). Then \(f\in C^\infty(\Omega)\).}
(ii)
Assume \(f\in C^\omega(\Omega)\). Then for each \(y\in \Omega\) there exists a neighborhood \(N(y)\) and positive constants \(M\), \(r\) such that
$$
f(x)=\sum_\alpha\frac{1}{\alpha!}(D^\alpha f(y))(x-y)^\alpha
$$
for all \(x\in N(y)\), and the series converges (absolutely) for each \(x\in N(y)\), and
$$
|D^\beta f(x)|\le M|\beta|!r^{-|\beta|}.
$$
The proof follows from Proposition A1.
An open set \(\Omega\in\mathbb{R}\) is called connected if \(\Omega\) is not a union of two nonempty
open sets with empty intersection. An open set \(\Omega\in\mathbb{R}\) is connected if and only if its path connected, see [11], pp. 38, for example. We say that \(\Omega\) is path connected if for any \(x,y\in\Omega\) there is a continuous curve \(\gamma(t)\in\Omega\), \(0\le t\le1\), with \(\gamma(0)=x\) and \(\gamma(1)=y\). From the theory of one complex variable we know that a continuation of an analytic function is uniquely determined. The same is true for real analytic functions.
Proposition A3. Assume \(f\in C^\omega(\Omega)\) and \(\Omega\) is connected. Then
\(f\) is uniquely determined if for one \(z\in\Omega\) all \(D^\alpha f(z)\) are known.
Proof. See F. John [10], p. 65. Suppose \(g, h\in C^\omega(\Omega)\) and
\(D^\alpha g(z)=D^\alpha h(z)\) for every \(\alpha\). Set \(f=g-h\) and
\begin{eqnarray*}
\Omega_1&=&\{x\in\Omega:\ D^\alpha f(x)=0\ \ \mbox{for all}\ \alpha\},\\
\Omega_2&=&\{x\in\Omega:\ D^\alpha f(x)\not=0\ \ \mbox{for at least one}\ \alpha\}.
\end{eqnarray*}
The set \(\Omega_2\) is open since \(D^\alpha f\) are continuous in \(\Omega\). The set \(\Omega_1\) is also open since \(f(x)=0\) in a neighbourhood of \(y\in\Omega_1\). This follows from
$$
f(x)=\sum_\alpha \frac{1}{\alpha!}(D^\alpha f(y))(x-y)^\alpha.
$$
Since \(z\in\Omega_1\), i. e., \(\Omega_1\not=\emptyset\), it follows \(\Omega_2=\emptyset\).
\(\Box\)
It was shown in Proposition A2 that derivatives of a real analytic function satisfy estimates.
On the other hand it follows, see the next proposition, that a function \(f\in C^\infty\) is real analytic if these estimates are satisfied.
Definition. Let \(y\in\Omega\) and \(M,\ r\) positive constants. Then \(f\) is said to be in the class \(C_{M,r}(y)\) if \(f\in C^\infty\) in a neighbourhood of \(y\) and if
$$
|D^\beta f(y)|\le M|\beta|!r^{-|\beta|}
$$
for all \(\beta\).
Proposition A4. \(f\in C^\omega(\Omega)\) if and only if \(f\in C^\infty(\Omega)\) and for every compact subset \(S\subset\Omega\) there are positive constants \(M,\;r\) such that
$$
f\in C_{M,r}(y)\ \ \mbox{for all}\ y\in S.
$$
Proof. See F. John [10], pp. 65-66. We will prove the local version of the proposition, that is, we show it for each fixed \(y\in\Omega\). The general version follows from Heine-Borel theorem. Because of Proposition A3 it remains to show that the Taylor series
$$
\sum_\alpha\frac{1}{\alpha!}D^\alpha f(y)(x-y)^\alpha
$$
converges (absolutely) in a neighborhood of \(y\) and that this series is equal to \(f(x)\).
Define a neighborhood of \(y\) by
$$
N_d(y)=\{x\in\Omega:\ \ |x_1-y_1|+\ldots+|x_n-y_n|<d\},
$$
where \(d\) is a sufficiently small positive constant. Set \(\Phi(t)=f(y+t(x-y))\). The one-dimensional Taylor theorem says
$$
f(x)=\Phi(1)=\sum_{k=0}^{j-1}\frac{1}{k!}\Phi^{(k)}(0)+r_j,
$$
where
$$
r_j=\frac{1}{(j-1)!}\int_0^1\ (1-t)^{j-1}\Phi^{(j)}(t)\ dt.
$$
From formula 7. for directional derivatives it follows for \(x\in N_d(y)\) that
$$
\frac{1}{j!}\frac{d^j}{dt^j}\Phi(t)=\sum_{|\alpha|=j}\frac{1}{\alpha!}D^\alpha f(y+t(x-y))(x-y)^\alpha.
$$
From the assumption and the multinomial formula 3. we get for \(0\le t\le 1\)
\begin{eqnarray*}
\left|\frac{1}{j!}\frac{d^j}{dt^j}\Phi(t)\right|&\le&M\sum_{|\alpha|=j}\frac{|\alpha|!}{\alpha!}r^{-|\alpha|}\left|(x-y)^\alpha\right|\\
&=& Mr^{-j}\left(|x_1-y_1|+\ldots +|x_n-y_n|\right)^j\\
&\le&M\left(\frac{d}{r}\right)^j.
\end{eqnarray*}
Choose \(d>0\) such that \(d<r\), then the Taylor series converges (absolutely) in \(N_d(y)\) and it is equal to \(f(x)\) since the remainder satisfies, see the above estimate,
$$
|r_j|=\left|\frac{1}{(j-1)!}\int_0^1\ (1-t)^{j-1}\Phi^j(t)\ dt\right|\le M\left(\frac{d}{r}\right)^j.
\]
\(\Box\)
We recall that the notation \(f<<F\) (\(f\) is majorized by \(F\)) was defined in the previous section.
Proposition A5. (i) \(f=(f_1,\ldots,f_m)\in C_{M,r}(0)\) if and only if \(f<<(\Phi,\ldots,\Phi)\), where
$$
\Phi(x)=\frac{Mr}{r-x_1-\ldots-x_n}\ .
$$}
(ii) \(f\in C_{M,r}(0)\) and \(f(0)=0\) if and only if
$$
f<<(\Phi-M,\ldots,\Phi-M),
$$
where
$$
\Phi(x)=\frac{M(x_1+\ldots+x_n)}{r-x_1-\ldots-x_n}\ .
$$
Proof.
$$
D^\alpha\Phi(0)=M|\alpha|!r^{-|\alpha|}.
\]
\(\Box\)
Remark. The definition of \(f<<F\) implies, trivially, that \(D^\alpha f<<D^\alpha F\).
The next proposition shows that compositions majorize if the involved functions majorize. More precisely, we have
Proposition A6. Let \(f,\ F:\ \mathbb{R}\mapsto\mathbb{R}^m\) and \(g,\ G\) maps a neighborhood of \(0\in\mathbb{R}^m\) into \({\mathbb R}^p\). Assume all functions \(f(x),\ F(x),\ g(u),\ G(u)\) are in \(C^\infty\), \(f(0)=F(0)=0\), \(f<<F\) and \(g<<G\). Then
\(g(f(x))<<G(F(x))\).}
Proof. See F. John [10], p. 68. Set
$$
h(x)=g(f(x)),\ \ \ H(x)=G(F(x)).
$$
For each coordinate \(h_k\) of \(h\) we have, according to the chain rule,
$$
D^\alpha h_k(0)=P_\alpha(\delta^\beta g_l(0),D^\gamma f_j(0)),
$$
where \(P_\alpha\) are polynomials with non-negative integers as coefficients, \(P_\alpha\)
are independent on \(g\) or \(f\) and \(\delta:=(\partial/\partial u_1,\ldots,\partial/\partial u_m)\). Thus,
\begin{eqnarray*}
|D^\alpha h_k(0)|&\le&P_\alpha(|\delta^\beta g_l(0)|,|D^\gamma f_j(0)|)\\
&\le&P_\alpha(\delta^\beta G_l(0),D^\gamma F_j(0))\\
&=&D^\alpha H_k(0).
\end{eqnarray*}
\(\Box\)
Using this result and Proposition A4, which characterizes real analytic functions, it follows that compositions of real analytic functions are real analytic functions again.
Proposition A7. Assume \(f(x)\) and \(g(u)\) are real analytic, then \(g(f(x))\) is real analytic if \(f(x)\) is in the domain of definition of \(g\).
Proof. See F. John [10], p. 68. Assume that \(f\) maps a neighborhood of \(y\in\mathbb{R}\) in \(\mathbb{R}^m\) and \(g\) maps a neighborhood of \(v=f(y)\) in ${\mathbb R}^m$. Then \(f\in C_{M,r}(y)\) and \(g\in C_{\mu,\rho}(v)\) implies
$$
h(x):=g(f(x))\in C_{\mu,\rho r/(mM+\rho)}(y).
$$
Once one has shown this inclusion, the proposition follows from Proposition~A4. To show the inclusion, we set
$$
h(y+x):=g(f(y+x))\equiv g(v+f(y+x)-f(x))=:g^*(f^*(x)),
$$
where \(v=f(y)\) and
\begin{eqnarray*}
g^*(u):&=&g(v+u)\in C_{\mu,\rho}(0)\\
f^*(x):&=&f(y+x)-f(y)\in C_{M,r}(0).
\end{eqnarray*}
In the above formulas \(v,\ y\) are considered as fixed parameters. From Proposition~A5 it follows
\begin{eqnarray*}
f^*(x)&<<&(\Phi-M,\ldots,\Phi-M)=:F\\
g^*(u)&<<&(\Psi,\ldots,\Psi)=:G,
\end{eqnarray*}
where
\begin{eqnarray*}
\Phi(x)&=&\frac{Mr}{r-x_1-x_2-\ldots-x_n}\\
\Psi(u)&=&\frac{\mu\rho}{\rho-x_1-x_2-\ldots-x_n}.
\end{eqnarray*}
From Proposition A6 we get
$$
h(y+x)<<(\chi(x),\ldots,\chi(x))\equiv G(F),
$$
where
\begin{eqnarray*}
\chi(x)&=&\frac{\mu\rho}{\rho-m(\Phi(x)-M)}\\
&=&\frac{\mu\rho(r-x_1-\ldots-x_n)}{\rho r-(\rho+mM)(x_1+\ldots+x_n)}\\
&<<&\frac{\mu\rho r}{\rho r-(\rho+mM)(x_1+\ldots+x_n)}\\
&=&\frac{\mu\rho r/(\rho+mM)}{\rho r/(\rho+mM)-(x_1+\ldots x_n)}.
\end{eqnarray*}
See an exercise for the ''\(<<\)''-inequality.
\(\Box\)
Contributors:
Integrated by Justin Marshall.


