4.1: One-Dimensional Wave Equation
- Page ID
- 2148
The one-dimensional wave equation is given by
\begin{equation}
\label{waveone}
\dfrac{1}{c^2}u_{tt}-u_{xx}=0,
\end{equation}
where \(u=u(x,t)\) is a scalar function of two variables and \(c\) is a positive constant. According to previous considerations, all \(C^2\)-solutions of the wave equation are
\begin{equation}
\label{wavegen}
u(x,t)=f(x+ct)+g(x-ct),
\end{equation}
with arbitrary \(C^2\)-functions \(f\) and \(g\)
The Cauchy initial value problem for the wave equation is to find a \(C^2\)-solution of
\begin{eqnarray*}
\dfrac{1}{c^2}u_{tt}-u_{xx}&=&0\\
u(x,0)&=&\alpha(x)\\
u_t(x,0)&=&\beta(x),
\end{eqnarray*}
where \(\alpha,\ \beta\in C^2(-\infty,\infty)\) are given.
Theorem 4.1. There exists a unique \(C^2(\mathbb{R}^1\times\mathbb{R}^1)\)-solution of the Cauchy initial value problem, and this solution is given by d'Alembert's1 formula
\begin{equation}
\label{waveform}
u(x,t)=\dfrac{\alpha(x+ct)+\alpha(x-ct)}{2}+\dfrac{1}{2c}\int_{x-ct}^{x+ct}\ \beta(s)\ ds.
\end{equation}
Proof. Assume there is a solution \(u(x,t)\) of the Cauchy initial value problem, then it follows from (\ref{wavegen}) that
\begin{eqnarray}
\label{ini1}
u(x,0)&=&f(x)+g(x)=\alpha(x)\\
\label{ini2}
u_t(x,0)&=&cf'(x)-cg'(x)=\beta(x).
\end{eqnarray}
From (\ref{ini1}) we obtain
\[f'(x)+g'(x)=\alpha'(x),\]
which implies, together with (\ref{ini2}), that
\[\begin{eqnarray*}
\label{12a} f'(x)&=&\dfrac{\alpha'(x)+\beta(x)/c}{2}\\
\label{12b}g'(x)&=&\dfrac{\alpha'(x)-\beta(x)/c}{2}.
\end{eqnarray*}\]
Then
\[\begin{eqnarray*}
f(x)&=&\dfrac{\alpha(x)}{2}+\dfrac{1}{2c}\int_0^x\ \beta(s)\ ds +C_1\\
g(x)&=&\dfrac{\alpha(x)}{2}-\dfrac{1}{2c}\int_0^x\ \beta(s)\ ds +C_2.
\end{eqnarray*}\]
The constants \(C_1\), \(C_2\) satisfy
\[C_1+C_2=f(x)+g(x)-\alpha(x)=0,\]
see (\ref{ini1}). Thus each \(C^2\)-solution of the Cauchy initial value problem is given by d'Alembert's formula. On the other hand, the function \(u(x,t)\) defined by the right hand side of (\ref{waveform}) is a solution of the initial value problem.
\(\Box\)
Corollaries. 1. The solution \(u(x,t)\) of the initial value problem depends on the values of \(\alpha\) at the endpoints of the interval \([x-ct,x+ct]\) and on the values of \(\beta\) on this interval only, see Figure 4.1.1. The interval \([x-ct,x+ct]\) is called {\it domain of dependence}.
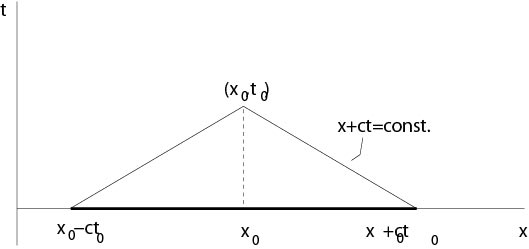
Figure 4.1.1: Interval of dependence
2. Let \(P\) be a point on the \(x\)-axis. Then we ask which points \((x,t)\) need values of \(\alpha\) or \(\beta\) at \(P\) in order to calculate \(u(x,t)\)? From the d'Alembert formula it follows that this domain is a cone, see Figure 4.2.1. This set is called domain of influence.
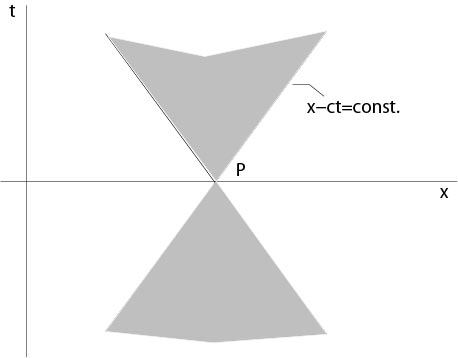
Figure 4.2.1: Domain of influence
1 d'Alembert, Jean Babtiste le Rond, 1717-1783
Contributors and Attributions
Integrated by Justin Marshall.


