5.1: Definition and Properties
- Page ID
- 2154
Definition. Let \(f\in C_0^s(\mathbb{R}^n)\), \(s=0,1,\ldots\). The function \(\hat{f}\) defined by
\begin{equation}
\label{four1}
\widehat{f}(\xi)=(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{-i\xi\cdot x}f(x)\ dx,
\end{equation}
where \(\xi\in\mathbb{R}^n\), is called {\it Fourier transform} of \(f\), and the function \(\widetilde{g}\)
given by
\begin{equation}
\label{invfour1}
\widetilde{g}(x)=(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{i\xi\cdot x}g(\xi)\ d\xi
\end{equation}
is called inverse Fourier transform, provided the integrals on the right hand side
exist.
From (\ref{four1}) it follows by integration by parts that differentiation of a function is changed to multiplication of its Fourier transforms, or an analytical operation is converted into an algebraic operation. More precisely, we have
Proposition 5.1.
$$
\widehat{D^\alpha f}(\xi)=i^{|\alpha|}\xi^\alpha\widehat{f}(\xi),
$$
where \(|\alpha|\le s\).
The following proposition shows that the Fourier transform of \(f\) decreases rapidly for \(|\xi|\to\infty\), provided \(f\in C_0^s(\mathbb{R}^n)\). In particular, the right hand side of (\ref{invfour1}) exists for \(g:=\hat{f}\) if \(f\in C_0^{n+1}(\mathbb{R}^n)\).
Proposition 5.2. Assume \(g\in C_0^s(\mathbb{R}^n)\), then there is a constant \(M=M(n,s,g)\) such that
$$
|\widehat{g}(\xi)|\le \frac{M}{(1+|\xi|)^s}.
\]
Proof. Let \(\xi=(\xi_1,\ldots,\xi_n)\) be fixed and let \(j\) be an index such that
\(|\xi_j|=\max_k |\xi_k|\). Then
$$
|\xi|=\left(\sum_{k=1}^n\xi_k^2\right)^{1/2}\le\sqrt{n}|\xi_j|
$$
which implies
\begin{eqnarray*}
(1+|\xi|)^s&=&\sum_{k=0}^s{s\choose k}|\xi|^k\\
&\le&2^s\sum_{k=0}^sn^{k/2}|\xi_j|^k\\
&\le&2^sn^{s/2}\sum_{|\alpha|\le s}|\xi^\alpha|.
\end{eqnarray*}
This inequality and Proposition 5.1 imply
\begin{eqnarray*}
(1+|\xi|)^s|\widehat{g}(\xi)|&\le&2^sn^{s/2}\sum_{|\alpha|\le s}|(i\xi)^\alpha\widehat{g}(\xi)|\\
&\le&2^sn^{s/2}\sum_{|\alpha|\le s}\int_{\mathbb{R}^n}\ |D^\alpha g(x)|\ dx=:M.
\end{eqnarray*}
\(\Box\)
The notation inverse Fourier transform for (\ref{invfour1}) is justified by
Theorem 5.1. \(\widetilde{\widehat{f}}=f\) and \(\widehat{\widetilde{f}}=f\).
Proof. See \cite{Yosida}, for example. We will prove the first assertion
\begin{equation}
\label{four2}
(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{i\xi\cdot x}\widehat{f}(\xi)\ d\xi=f(x)
\end{equation}
here. The proof of the other relation is left as an exercise. All integrals appearing in the following exist, see Proposition 5.2 and the special choice of \(g\).
(i) Formula
\begin{equation}
\label{four3}
\int_{\mathbb{R}^n}\ g(\xi)\widehat{f}(\xi)e^{ix\cdot\xi}\ d\xi=\int_{\mathbb{R}^n}\ \widehat{g}(y)f(x+y)\ dy
\end{equation}
follows by direct calculation:
\begin{eqnarray*}
&&\int_{\mathbb{R}^n}\ g(\xi)\left((2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{-ix\cdot y}f(y)\ dy\right)e^{i x\cdot\xi}\ d\xi\\
&&\qquad =(2\pi)^{-n/2}\int_{\mathbb{R}^n}\left(\int_{\mathbb{R}^n}\ g(\xi)e^{-i\xi\cdot(y-x)}\ d\xi\right)f(y)\ dy\\
&&\qquad =\int_{\mathbb{R}^n}\ \widehat{g}(y-x)f(y)\ dy\\
&&\qquad=\int_{\mathbb{R}^n}\ \widehat{g}(y)f(x+y)\ dy.
\end{eqnarray*}
(ii) Formula
\begin{equation}
\label{four4}
(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{-i y\cdot\xi}g(\varepsilon\xi)\ d\xi=\varepsilon^{-n}\widehat{g}(y/\varepsilon)
\end{equation}
for each \(\varepsilon>0\) follows after substitution \(z=\varepsilon\xi\) in the left hand side of (\ref{four1}).
(iii) Equation
\begin{equation}
\label{four5}
\int_{\mathbb{R}^n}\ g(\varepsilon\xi)\widehat{f}(\xi)e^{i x\cdot \xi}\ d\xi=\int_{\mathbb{R}^n}\ \widehat{g}(y)f(x+\varepsilon y)\ dy
\end{equation}
follows from (\ref{four3}) and (\ref{four4}). Set \(G(\xi):=g(\varepsilon\xi)\), then (\ref{four3}) implies
$$
\int_{\mathbb{R}^n}\ G(\xi)\widehat{f}(\xi)e^{i x\cdot\xi}\ d\xi=\int_{\mathbb{R}^n}\ \widehat{G}(y)f(x+y)\ dy.
$$
Since, see (\ref{four4}),
\begin{eqnarray*}
\widehat{G}(y)&=&(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{-iy\cdot\xi}g(\varepsilon\xi)\ d\xi\\
&=&\varepsilon^{-n}\widehat{g}(y/\varepsilon),
\end{eqnarray*}
we arrive at
\begin{eqnarray*}
\int_{\mathbb{R}^n}\ g(\varepsilon\xi)\widehat{f}(\xi)&=&\int_{\mathbb{R}^n}\varepsilon^{-n}\widehat{g}(y/\varepsilon)f(x+y)\ dy\\
&=&\int_{\mathbb{R}^n}\widehat{g}(z)f(x+\varepsilon z)\ dz.
\end{eqnarray*}
Letting \(\varepsilon\to 0\), we get
\begin{equation}
\label{four6}
g(0)\int_{\mathbb{R}^n}\ \widehat{f}(\xi)e^{i x\cdot\xi}\ d\xi=f(x)\int_{\mathbb{R}^n}\ \widehat{g}(y)\ dy.
\end{equation}
Set
$$
g(x):=e^{-|x|^2/2},
$$
then
\begin{equation}
\label{four7}
\int_{\mathbb{R}^n}\ \widehat{g}(y)\ dy=(2\pi)^{n/2}.
\end{equation}
Since \(g(0)=1\), the first assertion of Theorem 5.1 follows from (\ref{four6}) and (\ref{four7}). It remains to show (\ref{four7}).
(iv) Proof of (\ref{four7}). We will show
\begin{eqnarray*}
\widehat{g}(y):&=&(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ e^{-|x|^2/2}e^{-ix\cdot x}\ dx\\
&=&e^{-|y|^2/2}.
\end{eqnarray*}
The proof of
$$
\int_{\mathbb{R}^n}\ e^{-|y|^2/2}\ dy=(2\pi)^{n/2}
$$
is left as an exercise. Since
$$
-\left(\frac{x}{\sqrt{2}}+i\frac{y}{\sqrt{2}}\right)\cdot\left(\frac{x}{\sqrt{2}}+i\frac{y}{\sqrt{2}}\right)=-\left(\frac{|x|^2}{2}+i x\cdot y-\frac{|y|^2}{2}\right)
$$
it follows
\begin{eqnarray*}
\int_{\mathbb{R}^n}\ e^{-|x|^2/2}e^{-ix\cdot y}\ dx&=&\int_{\mathbb{R}^n}\ e^{-\eta^2}e^{-|y|^2/2}\ dx\\
&=&e^{-|y|^2/2}\int_{\mathbb{R}^n}\ e^{-\eta^2}\ dx\\
&=&2^{n/2}e^{-|y|^2/2}\int_{\mathbb{R}^n}\ e^{-\eta^2}\ d\eta
\end{eqnarray*}
where
$$
\eta:=\frac{x}{\sqrt{2}}+i\frac{y}{\sqrt{2}}.
$$
Consider first the one-dimensional case. According to Cauchy's theorem we have
$$
\oint_C\ e^{-\eta^2}\ d\eta=0,
$$
where the integration is along the curve \(C\) which is the union of four curves as indicated in Figure \ref{fourfig}.
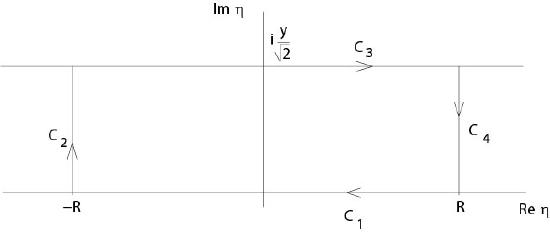
Figure 5.1.1: Proof of (\ref{four7})
Consequently
$$
\int_{C_3}\ e^{-\eta^2}\ d\eta=\frac{1}{\sqrt{2}}\int_{-R}^R\ e^{-x^2/2}\ dx-\int_{C_2}\ e^{-\eta^2}\ d\eta-\int_{C_4}\ e^{-\eta^2}\ d\eta.
$$
It follows
$$
\lim_{R\to\infty}\int_{C_3}\ e^{-\eta^2}\ d\eta=\sqrt{\pi}
$$
since
$$
\lim_{R\to\infty}\int_{C_k}\ e^{-\eta^2}\ d\eta=0,\ \ k=2,\ 4.
$$
The case \(n>1\) can be reduced to the one-dimensional case as follows. Set
$$
\eta=\frac{x}{\sqrt{2}}+i\frac{y}{\sqrt{2}}=(\eta_1,\ldots,\eta_n),
$$
where
$$
\eta_l=\frac{x_l}{\sqrt{2}}+i\frac{y_l}{\sqrt{2}}.
$$
From \(d\eta=d\eta_1\ldots d\eta_l\) and
$$
e^{-\eta^2}=e^{-\sum_{l=1}^n\eta_l^2}=\prod_{l=1}^ne^{-\eta_l^2}
$$
it follows
$$
\int_{\mathbb{R}^n}\ e^{-eta^2}\ d\eta=\prod_{l=1}^n\int_{\Gamma_l}\ e^{-\eta_l^2}\ d\eta_l,
$$
where for fixed \(y\)
$$
\Gamma_l=\{z\in{\mathbb C}:\ z=\frac{x_l}{\sqrt{2}}+i\frac{y_l}{\sqrt{2}}, -\infty<x_l<+\infty\}.
\]
\(\Box\)
There is a useful class of functions for which the integrals in the definition of \(\widehat{f}\) and \(\widetilde{f}\) exist.
For \(u\in C^\infty(\mathbb{R}^n)\) we set
$$
q_{j,k}(u):=\max_{\alpha:\ |\alpha|\le k}\left(\sup_{\mathbb{R}^n}\left((1+|x|^2)^{j/2}|D^\alpha u(x)|\right)\right).
\]
Definition. The Schwartz class of rapidly decreasing functions is
$$
{\mathcal{S}}(\mathbb{R}^n)=\left\{u\in C^\infty(\mathbb{R}^n): \ q_{j,k}(u)<\infty\ \mbox{for any}\ j,k\in{\mathbb N}\cup\{0\}\right\}.
\]
This space is a Frechét space.
Proposition 5.3. Assume \(u\in{\mathcal{S}}(\mathbb{R}^n)\), then \(\widehat{u}\) and \(\widetilde{u}\in{\mathcal{S}}(\mathbb{R}^n)\).
Proof. See [24], Chapter 1.2, for example, or an exercise.
Contributors and Attributions
Integrated by Justin Marshall.


