4.2: Arc Length
- Page ID
- 3325
In Section 4.1 we saw that one revolution has a radian measure of \(2\pi \) rad. Note that \(2\pi\) is the ratio of the circumference (i.e. total arc length) \(C \) of a circle to its radius \(r\):
\[ \text{Radian measure of 1 revolution} ~=~ 2\pi ~=~ \frac{2\pi\,r}{r} ~=~
\frac{C}{r} ~=~ \frac{\text{total arc length}}{\text{radius}}
\nonumber \]
Clearly, that ratio is independent of \(r \). In general, the radian measure of an angle is the ratio of the arc length cut off by the corresponding central angle in a circle to the radius of the circle, independent of the radius.
To see this, recall our formal definition of a radian: the central angle in a circle of radius \(r\) which intercepts an arc of length \(r \). So suppose that we have a circle of radius \(r \) and we place a central angle with radian measure \(1 \) on top of another central angle with radian measure \(1 \), as in Figure 4.2.1(a). Clearly, the combined central angle of the two angles has radian measure \(1+1=2 \), and the combined arc length is \(r+r=2r \).
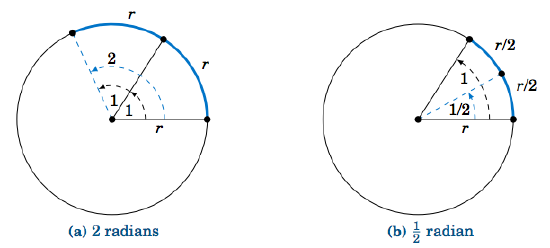
Now suppose that we cut the angle with radian measure \(1 \) in half, as in Figure 4.2.1(b). Clearly, this cuts the arc length \(r \) in half as well. Thus, we see that
\[\nonumber \begin{align}
\text{Angle} ~&=~ 1~\text{radian} \quad&\Rightarrow\quad \text{arc length} ~&=~ r ~,\\ \nonumber
\text{Angle} ~&=~ 2~\text{radians} \quad&\Rightarrow\quad \text{arc length} ~&=~ 2\,r ~,\\ \nonumber
\text{Angle} ~&=~ \tfrac{1}{2}~\text{radian} \quad&\Rightarrow\quad \text{arc length} ~&=~
\tfrac{1}{2}\,r ~,\end{align} \nonumber \]
and in general, for any \(\theta \ge 0 \),
\[\nonumber \text{Angle} ~=~ \theta~\text{radians} \quad \Rightarrow\quad \text{arc length} ~=~ \theta\,r ~,
\nonumber \]
so that
\[ \theta ~=~ \frac{\text{arc length}}{\text{radius}} ~~.
\nonumber \]
Intuitively, it is obvious that shrinking or magnifying a circle preserves the measure of a central angle even as the radius changes. The above discussion says more, namely that the ratio of the length \(s \) of an intercepted arc to the radius \(r \) is preserved, precisely because that ratio is the measure of the central angle in radians (see Figure 4.2.2).
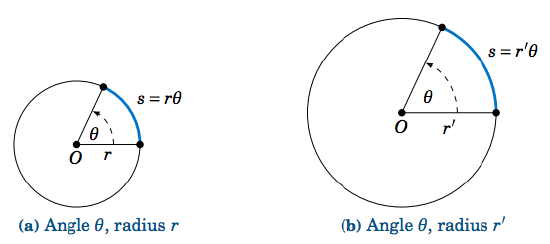
We thus get a simple formula for the length of an arc:
In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \). Then the arc length \(s \) is:
\[ s ~=~ r\,\theta \label{4.4} \]
In a circle of radius \(r=2 \) cm, what is the length \(s \) of the arc intercepted by a central angle of measure \(\theta = 1.2 \) rad?
Solution
Using Equation \ref{4.4}, we get:
\[s ~=~ r\,\theta ~=~ (2)\,(1.2) ~=~ \boxed{2.4~\text{cm}} \nonumber \]
In a circle of radius \(r=10 \) ft, what is the length \(s \) of the arc intercepted by a central angle of measure \(\theta = 41^\circ\;\)?
Solution
Using Equation \ref{4.4} blindly with \(\theta = 41^\circ \), we would get \(\;s = r\,\theta = (10)\,(41) = 410 \) ft. But this impossible, since a circle of radius \(10 \) ft has a circumference of only \(2\pi\,(10) \approx 62.83 \) ft! Our error was in using the angle \(\theta \) measured in degrees, not radians. So first convert \(\theta =41^\circ \) to radians, then use \(s=r\,\theta\):
\[\theta = 41^\circ ~=~ \frac{\pi}{180} \;\cdot\; 41 ~=~ 0.716~\text{rad}
\quad\Rightarrow\quad s ~=~ r\,\theta ~=~ (10)\,(0.716) ~=~ \boxed{7.16~\text{ft}}\nonumber \]
Note that since the arc length \(s \) and radius \(r \) are usually given in the same units, radian measure is really unitless, since you can think of the units canceling in the ratio \(\frac{s}{r} \), which is just \(\theta \). This is another reason why radians are so widely used.
A central angle in a circle of radius \(5 \) m cuts off an arc of length \(2 \) m. What is the measure of the angle in radians? What is the measure in degrees?
Solution
Letting \(r=5 \) and \(s=2 \) in Equation \ref{4.4}, we get:
\[\theta ~=~ \frac{s}{r} ~=~ \frac{2}{5} ~=~ \boxed{0.4~\text{rad}}\nonumber \]
In degrees, the angle is:
\[ \theta = 0.4~\text{rad} ~=~ \frac{180}{\pi} \;\cdot\; 0.4 ~=~ \boxed{22.92^\circ}\nonumber \]
For central angles \(\theta > 2\pi \) rad, i.e. \(\theta > 360^\circ \), it may not be clear what is meant by the intercepted arc, since the angle is larger than one revolution and hence "wraps around'' the circle more than once. We will take the approach that such an arc consists of the full circumference plus any additional arc length determined by the angle. In other words, Equation \ref{4.4} is still valid for angles \(\theta > 2\pi \) rad.
What about negative angles? In this case using \(s=r\,\theta \) would mean that the arc length is negative, which violates the usual concept of length. So we will adopt the convention of only using nonnegative central angles when discussing arc length.
A rope is fastened to a wall in two places \(8 \) ft apart at the same height. A cylindrical container with a radius of \(2 \) ft is pushed away from the wall as far as it can go while being held in by the rope, as in Figure 4.2.3 which shows the top view. If the center of the container is \(3 \) feet away from the point on the wall midway between the ends of the rope, what is the length \(L \) of the rope?
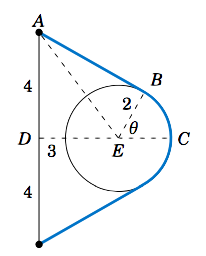
Solution:
We see that, by symmetry, the total length of the rope is \(\;L = 2\;(AB + \overparen{BC}) \). Also, notice that \(\triangle\,ADE \) is a right triangle, so the hypotenuse has length \(AE = \sqrt{DE^2 + DA^2} = \sqrt{3^2 + 4^2} = 5 \) ft, by the Pythagorean Theorem. Now since \(\overline{AB} \) is tangent to the circular container, we know that \(\angle\,ABE \) is a right angle. So by the Pythagorean Theorem we have
\[ AB ~=~ \sqrt{AE^2 - BE^2} ~=~ \sqrt{5^2 - 2^2} ~=~ \sqrt{21} ~\text{ft}. \nonumber \]
By Equation \ref{4.4} the arc \(\overparen{BC} \) has length \(BE \cdot \theta \), where \(\theta = \angle\,BEC \) is the supplement of \(\angle\,AED + \angle\,AEB \). So since
\[ \tan\,\angle\,AED ~=~ \frac{4}{3} ~\Rightarrow~ \angle\,AED ~=~ 53.1^\circ \quad\text{and}\quad
\cos\,\angle\,AEB ~=~ \frac{BE}{AE} ~=~ \frac{2}{5} ~\Rightarrow~ \angle\,AEB ~=~ 66.4^\circ ~,
\nonumber \]
we have
\[ \nonumber
\theta ~=~ \angle\,BEC ~=~ 180^\circ \;-\; (\angle\,AED + \angle\,AEB) ~=~ 180^\circ \;-\;
(53.1^\circ + 66.4^\circ) ~=~ 60.5^\circ ~.
\nonumber \]
Converting to radians, we get \(\;\theta = \frac{\pi}{180} \;\cdot\; 60.5 = 1.06 \) rad. Thus,
\[ L ~=~ 2\,(AB \;+\; \cdot \overparen{BC}) ~=~ 2\,(\sqrt{21} \;+\; BE \cdot \theta) ~=~
2\,(\sqrt{21} \;+\; (2)\,( 1.06)) ~=~ \boxed{13.4 ~\text{ft}} ~.
\nonumber \]
The centers of two belt pulleys, with radii of \(5 \) cm and \(8 \) cm, respectively, are \(15 \) cm apart. Find the total length \(L \) of the belt around the pulleys.
Solution
In Figure 4.2.4 we see that, by symmetry, \(\;L = 2\;(\overparen{DE} + EF + \overparen{FG}) \).
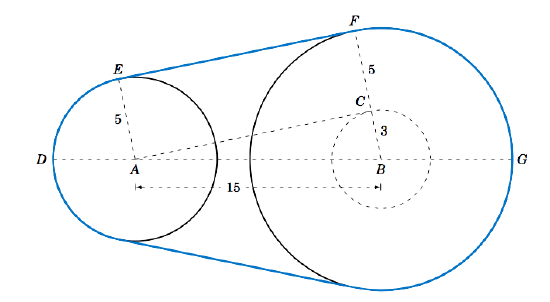
First, at the center \(B \) of the pulley with radius \(8 \), draw a circle of radius \(3 \), which is the difference in the radii of the two pulleys. Let \(C \) be the point where this circle intersects \(\overline{BF} \). Then we know that the tangent line \(\overline{AC} \) to this smaller circle is perpendicular to the line segment \(\overline{BF} \). Thus, \(\angle\,ACB \) is a right angle, and so the length of \(\overline{AC} \) is
\[AC ~=~ \sqrt{AB^2 - BC^2} ~=~ \sqrt{15^2 - 3^2} ~=~ \sqrt{216} ~=~ 6\,\sqrt{6}\nonumber \]
by the Pythagorean Theorem. Now since \(\overline{AE} \perp \overline{EF} \) and \(\overline{EF} \perp \overline{CF} \) and \(\overline{CF} \perp \overline{AC} \), the quadrilateral \(AEFC \) must be a rectangle. In particular, \(EF = AC \), so \(EF = 6\,\sqrt{6} \).
By Equation \ref{4.4} we know that \(\;\overparen{DE} = EA \cdot \angle\,DAE\; \) and \(\;\overparen{FG} = BF \cdot \angle\,GBF \), where the angles are measured in radians. So thinking of angles in radians (using \(\pi \) rad \(= 180^\circ\)), we see from Figure 4.2.4 that
\[\nonumber \angle\,DAE ~=~ \pi \;-\; \angle\,EAC \;-\; \angle\,BAC ~=~ \pi \;-\; \frac{\pi}{2} \;-\;
\angle\,BAC ~=~ \frac{\pi}{2} \;-\; \angle\,BAC ~, \nonumber \]
where
\[\nonumber \sin\;\angle\,BAC ~=~ \frac{BC}{AB} ~=~ \frac{3}{15} ~=~ 0.2 \quad\Rightarrow\quad
\angle\,BAC ~=~ 0.201~\text{rad.} \nonumber \]
Thus, \(\;\angle\,DAE = \frac{\pi}{2} \,-\, 0.201 = 1.37 \) rad. So since \(\overline{AE} \) and \(\overline{BF} \) are parallel, we have \(\;\angle\,ABC = \angle\,DAE = 1.37 \) rad. Thus, \(\;\angle\,GBF = \pi \,-\, \angle\,ABC = \pi \,-\, 1.37 = 1.77 \) rad. Hence,
\[\nonumber L ~=~ 2\;(\overparen{DE} \;+\; EF \;+\; \overparen{FG}) ~=~ 2\;(5\;(1.37) \;+\; 6\,\sqrt{6} \;+\;
8\;(1.77)) ~=~ \boxed{71.41~\text{cm}} ~. \nonumber \]


