8.2: Non-right Triangles - Law of Cosines
- Last updated
- Save as PDF
- Page ID
- 1376
Learning Objectives
In this section, you will:
- Use the Law of Cosines to solve oblique triangles.
- Solve applied problems using the Law of Cosines.
- Use Heron’s formula to find the area of a triangle.
Suppose a boat leaves port, travels \(10\) miles, turns \(20\) degrees, and travels another 8 miles as shown in Figure \(\PageIndex{1}\) How far from port is the boat?
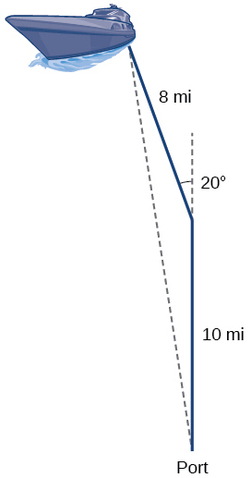
Figure \(\PageIndex{1}\)
Unfortunately, while the Law of Sines enables us to address many non-right triangle cases, it does not help us with triangles where the known angle is between two known sides, a SAS (side-angle-side) triangle, or when all three sides are known, but no angles are known, a SSS (side-side-side) triangle. In this section, we will investigate another tool for solving oblique triangles described by these last two cases.
Using the Law of Cosines to Solve Oblique Triangles
The tool we need to solve the problem of the boat’s distance from the port is the Law of Cosines, which defines the relationship among angle measurements and side lengths in oblique triangles. Three formulas make up the Law of Cosines. At first glance, the formulas may appear complicated because they include many variables. However, once the pattern is understood, the Law of Cosines is easier to work with than most formulas at this mathematical level.
Understanding how the Law of Cosines is derived will be helpful in using the formulas. The derivation begins with the Generalized Pythagorean Theorem, which is an extension of the Pythagorean Theorem to non-right triangles. Here is how it works: An arbitrary non-right triangle \(ABC\) is placed in the coordinate plane with vertex \(A\) at the origin, side \(c\) drawn along the x-axis, and vertex \(C\) located at some point \((x,y)\) in the plane, as illustrated in Figure \(\PageIndex{2}\). Generally, triangles exist anywhere in the plane, but for this explanation we will place the triangle as noted.
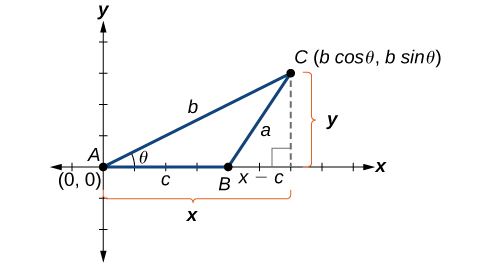
Figure \(\PageIndex{2}\)
We can drop a perpendicular from \(C\) to the x-axis (this is the altitude or height). Recalling the basic trigonometric identities, we know that
\(\cos \theta=\dfrac{x(adjacent)}{b(hypotenuse)}\) and \(\sin \theta=\dfrac{y(opposite)}{b(hypotenuse)}\)
In terms of \(\theta\), \(x=b \cos \theta\) and \(y=b \sin \theta\). The \((x,y)\) point located at \(C\) has coordinates \((b \cos \theta, b \sin \theta)\). Using the side \((x−c)\) as one leg of a right triangle and \(y\) as the second leg, we can find the length of hypotenuse \(a\) using the Pythagorean Theorem. Thus,
\(\begin{array}{ll} a^2={(x−c)}^2+y^2 \\[4pt] \;\;\;\;\; ={(b \cos \theta−c)}^2+{(b \sin \theta)}^2 & \text{Substitute }(b \cos \theta) \text{ for }x \text{ and }(b \sin \theta)\text{ for }y \\[4pt] \;\;\;\;\;\; =(b^2{\cos}^2 \theta−2bc \cos \theta+c^2)+b^2 {\sin}^2 \theta & \text{Expand the perfect square.} \\[4pt] \;\;\;\;\; =b^2{\cos}^2 \theta+b^2{\sin}^2 \theta+c^2−2bc \cos \theta & \text{Group terms noting that }{\cos}^2 \theta+{\sin}^2 \theta=1 \\[4pt] \;\;\;\;\; =b^2({\cos}^2 \theta+{\sin}^2 \theta)+c^2−2bc \cos \theta & \text{Factor out }b^2 \\[4pt]
a^2=b^2+c^2−2bc \cos \theta \end{array}\)
The formula derived is one of the three equations of the Law of Cosines. The other equations are found in a similar fashion.
Keep in mind that it is always helpful to sketch the triangle when solving for angles or sides. In a real-world scenario, try to draw a diagram of the situation. As more information emerges, the diagram may have to be altered. Make those alterations to the diagram and, in the end, the problem will be easier to solve.
The LAW OF COSINES
The Law of Cosines states that the square of any side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle.
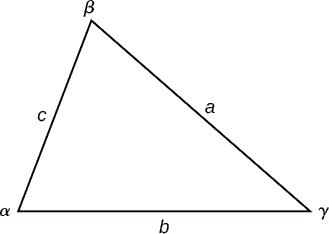
Figure \(\PageIndex{3}\)
For triangles labeled as in Figure \(\PageIndex{3}\), with angles \(\alpha\), \(\beta\) and \(\gamma\), and opposite corresponding sides \(a\), \(b\), and \(c\), respectively, the Law of Cosines is given as three equations.
\[a^2=b^2+c^2−2bc \cos \alpha\]
\[b^2=a^2+c^2−2ac \cos \beta\]
\[c^2=a^2+b^2−2ab \cos \gamma\]
To solve for a missing side measurement, the corresponding opposite angle measure is needed.
When solving for an angle, the corresponding opposite side measure is needed. We can use another version of the Law of Cosines to solve for an angle.
\[\cos \alpha=\dfrac{b^2+c^2−a^2}{2bc}\]
\[\cos \beta=\dfrac{a^2+c^2−b^2}{2ac}\]
\[\cos \gamma=\dfrac{a^2+b^2−c^2}{2ab}\]
How to: Given two sides and the angle between them (SAS), find the measures of the remaining side and angles of a triangle
- Sketch the triangle. Identify the measures of the known sides and angles. Use variables to represent the measures of the unknown sides and angles.
- Apply the Law of Cosines to find the length of the unknown side or angle.
- Apply the Law of Sines or Cosines to find the measure of a second angle.
- Compute the measure of the remaining angle.
Example \(\PageIndex{1}\): Finding the Unknown Side and Angles of a SAS Triangle
Find the unknown side and angles of the triangle in Figure \(\PageIndex{4}\).
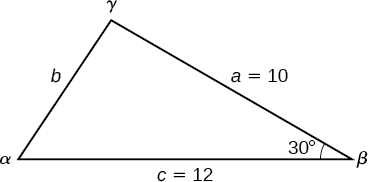
Figure \(\PageIndex{4}\)
Solution
First, make note of what is given: two sides and the angle between them. This arrangement is classified as SAS and supplies the data needed to apply the Law of Cosines.
Each one of the three laws of cosines begins with the square of an unknown side opposite a known angle. For this example, the first side to solve for is side \(b\), as we know the measurement of the opposite angle \(\beta\).
\(\begin{array}{ll} b^2=a^2+c^2−2ac \cos \beta \\[4pt] b^2={10}^2+{12}^2−2(10)(12)\cos(30°) & \text{Substitute the measurements for the known quantities.} \\[4pt] b^2=100+144−240 \left(\dfrac{\sqrt{3}}{2}\right) & \text{Evaluate the cosine and begin to simplify.} \\[4pt] b^2=244−120\sqrt{3} \\[4pt] b=\sqrt{244−120\sqrt{3}} & \text{Use the square root property.} \\[4pt] b≈6.013 \end{array}\)
Because we are solving for a length, we use only the positive square root. Now that we know the length \(b\), we can use the Law of Sines to fill in the remaining angles of the triangle. Solving for angle \(\alpha\), we have
\(\begin{array}{cc} \dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b} \\[4pt] \dfrac{\sin \alpha}{10}=\dfrac{\sin(30°)}{6.013} \\[4pt] \sin \alpha=\dfrac{10\sin(30°)}{6.013} & \text{Multiply both sides of the equation by }10. \\[4pt] \alpha={\sin}^{−1}\left(\dfrac{10\sin(30°)}{6.013}\right) & \text{Find the inverse sine of } \dfrac{10\sin(30°)}{6.013}. \\[4pt] \alpha≈56.3° \end{array}\)
The other possibility for \(\alpha\) would be \(\alpha=180°-56.3°≈123.7°\). In the original diagram,\(\alpha\) is adjacent to the longest side, so \(\alpha\) is an acute angle and, therefore, \(123.7°\) does not make sense. Notice that if we choose to apply the Law of Cosines, we arrive at a unique answer. We do not have to consider the other possibilities, as cosine is unique for angles between \(0°\) and \(180°\). Proceeding with \(\alpha≈56.3°\), we can then find the third angle of the triangle.
\[\begin{align*} \gamma&= 180^{\circ}-30^{\circ}-56.3^{\circ}\\ &\approx 93.7^{\circ} \end{align*}\]
The complete set of angles and sides is
\(\alpha≈56.3°\) \(a=10\)
\(\beta=30°\) \(b≈6.013\)
\(\gamma≈93.7°\) \(c=12\)
Exercise \(\PageIndex{1}\)
Find the missing side and angles of the given triangle: \(\alpha=30°\), \(b=12\), \(c=24\).
- Answer
-
\(a≈14.9\), \(\beta≈23.8°\), \(\gamma≈126.2°\).
Example \(\PageIndex{2}\): Solving for an Angle of a SSS Triangle
Find the angle \(\alpha\) for the given triangle if side \(a=20\), side \(b=25\), and side \(c=18\).
Solution
For this example, we have no angles. We can solve for any angle using the Law of Cosines. To solve for angle \(\alpha\), we have
\(\begin{array}{ll} a^2=b^2+c^2−2bc \cos \alpha \\[4pt] {20}^2={25}^2+{18}^2−2(25)(18)\cos \alpha & \text{Substitute the appropriate measurements.} \\[4pt] 400=625+324−900 \cos \alpha & \text{ Simplify in each step.} \\[4pt] 400=949−900 \cos \alpha \\[4pt] −549=−900 \cos \alpha & \text{Isolate }\cos \alpha. \\[4pt] 0.61≈\cos \alpha & \text{Find the inverse cosine.} \\[4pt] \alpha≈52.4° \end{array}\)
See Figure \(\PageIndex{5}\).
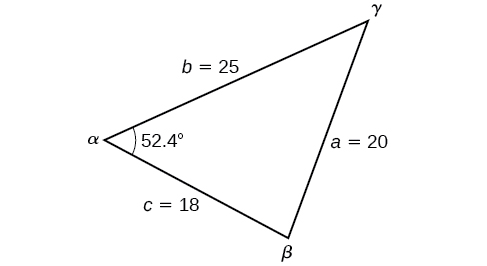
Figure \(\PageIndex{5}\)
Analysis
Because the inverse cosine can return any angle between \(0\) and \(180\) degrees, there will not be any ambiguous cases using this method.
Exercise \(\PageIndex{2}\)
Given \(a=5\), \(b=7\), and \(c=10\), find the missing angles.
- Answer
-
\(\alpha≈27.7°\), \(\beta≈40.5°\), \(\gamma≈111.8°\)
Solving Applied Problems Using the Law of Cosines
Just as the Law of Sines provided the appropriate equations to solve a number of applications, the Law of Cosines is applicable to situations in which the given data fits the cosine models. We may see these in the fields of navigation, surveying, astronomy, and geometry, just to name a few.
Example \(\PageIndex{3A}\): Using the Law of Cosines to Solve a Communication Problem
On many cell phones with GPS, an approximate location can be given before the GPS signal is received. This is accomplished through a process called triangulation, which works by using the distances from two known points. Suppose there are two cell phone towers within range of a cell phone. The two towers are located \(6000\) feet apart along a straight highway, running east to west, and the cell phone is north of the highway. Based on the signal delay, it can be determined that the signal is \(5050\) feet from the first tower and \(2420\) feet from the second tower. Determine the position of the cell phone north and east of the first tower, and determine how far it is from the highway.
Solution
For simplicity, we start by drawing a diagram similar to Figure \(\PageIndex{6}\) and labeling our given information.
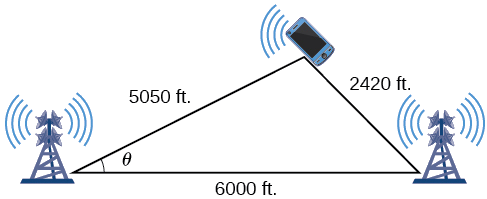
Figure \(\PageIndex{6}\)
Using the Law of Cosines, we can solve for the angle \(\theta\). Remember that the Law of Cosines uses the square of one side to find the cosine of the opposite angle. For this example, let \(a=2420\), \(b=5050\), and \(c=6000\). Thus, \(\theta\) corresponds to the opposite side \(a=2420\).
\[\begin{align*} a^2 & =b^2+c^2−2bc \cos \theta \\[4pt] {(2420)}^2 &={(5050)}^2+{(6000)}^2−2(5050)(6000) \cos \theta \\[4pt] \cos \theta &≈ 0.9183 \\[4pt] \theta &≈ {\cos}^{−1}(0.9183) \\[4pt] \theta &≈ 23.3° \end{align*}\]
To answer the questions about the phone’s position north and east of the tower, and the distance to the highway, drop a perpendicular from the position of the cell phone, as in Figure \(\PageIndex{7}\). This forms two right triangles, although we only need the right triangle that includes the first tower for this problem.
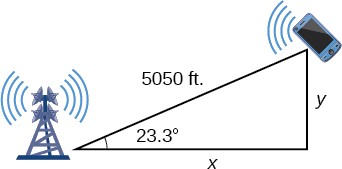
Figure \(\PageIndex{7}\)
Using the angle \(\theta=23.3\)° and the basic trigonometric identities, we can find the solutions. Thus
\[\begin{align*} \cos(23.3°) &= \dfrac{x}{5050} \\[4pt] x &= 5050\cos(23.3°) \\[4pt] x &≈ 4638.15\, feet\\[4pt] \sin(23.3°) &= \dfrac{y}{5050} \\[4pt] y &= 5050\sin(23.3°) \\[4pt] y &≈1997.5 \, feet \end{align*}\]
The cell phone is approximately \(4638\) feet east and \(1998\) feet north of the first tower, and \(1998\) feet from the highway.
Example \(\PageIndex{3B}\): Calculating Distance Traveled Using a SAS Triangle
Returning to our problem at the beginning of this section, suppose a boat leaves port, travels \(10\) miles, turns \(20\) degrees, and travels another \(8\) miles. How far from port is the boat? The diagram is repeated here in Figure \(\PageIndex{8}\).
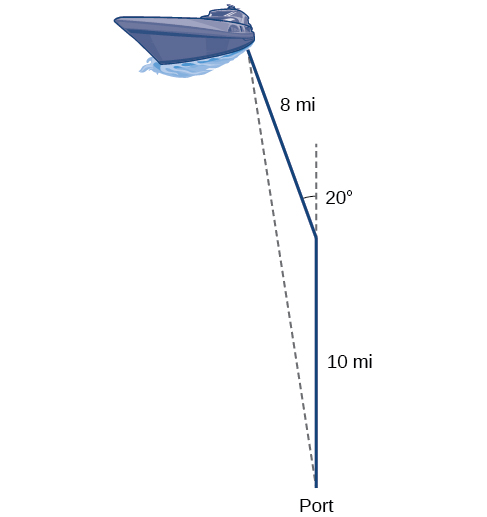
Figure \(\PageIndex{8}\)
Solution
The boat turned 20 degrees, so the obtuse angle of the non-right triangle is the supplemental angle, \(180°−20°=160°\). With this, we can utilize the Law of Cosines to find the missing side of the obtuse triangle—the distance of the boat to the port.
\[\begin{align*} x^2 &= 8^2+{10}^2−2(8)(10)\cos(160°) \\[4pt] x^2 &= 314.35 \\[4pt] x &= \sqrt{314.35} \\[4pt] x&≈17.7\, miles \end{align*}\]
The boat is about \(17.7\) miles from port.
Using Heron’s Formula to Find the Area of a Triangle
We already learned how to find the area of an oblique triangle when we know two sides and an angle. We also know the formula to find the area of a triangle using the base and the height. When we know the three sides, however, we can use Heron’s formula instead of finding the height. Heron of Alexandria was a geometer who lived during the first century A.D. He discovered a formula for finding the area of oblique triangles when three sides are known.
HERON’S FORMULA
Heron’s formula finds the area of oblique triangles in which sides \(a\), \(b\),and \(c\) are known.
\[Area=\sqrt{s(s−a)(s−b)(s−c)}\]
where \(s=\dfrac{(a+b+c)}{2}\) is one half of the perimeter of the triangle, sometimes called the semi-perimeter.
Example \(\PageIndex{4}\): Using Heron’s Formula to Find the Area of a Given Triangle
Find the area of the triangle in Figure \(\PageIndex{9}\) using Heron’s formula.
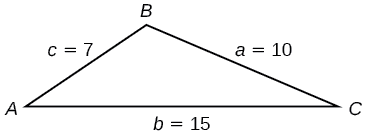
Figure \(\PageIndex{9}\)
Solution
First, we calculate \(s\).
\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \end{align*}\]
Then we apply the formula.
\[\begin{align*} Area&= \sqrt{s(s-a)(s-b)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\\ Area&\approx 29.4 \end{align*}\]
The area is approximately \(29.4\) square units.
Exercise \(\PageIndex{3}\)
Use Heron’s formula to find the area of a triangle with sides of lengths \(a=29.7\) ft, \(b=42.3\) ft, and \(c=38.4\) ft.
- Answer
-
Area = \(552\) square feet
Example \(\PageIndex{5}\): Applying Heron’s Formula to a Real-World Problem
A Chicago city developer wants to construct a building consisting of artist’s lofts on a triangular lot bordered by Rush Street, Wabash Avenue, and Pearson Street. The frontage along Rush Street is approximately \(62.4\) meters, along Wabash Avenue it is approximately \(43.5\) meters, and along Pearson Street it is approximately \(34.1\) meters. How many square meters are available to the developer? See Figure \(\PageIndex{10}\) for a view of the city property.
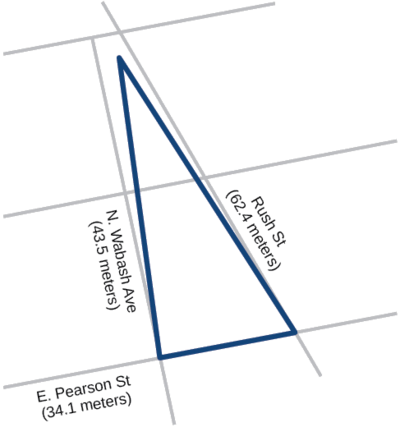
Figure \(\PageIndex{10}\)
Solution
Find the measurement for \(s\), which is one-half of the perimeter.
\[\begin{align*} s&= \dfrac{(62.4+43.5+34.1)}{2}\\ s&= 70\; m\\ \text {Apply Heron's formula.}\\ Area&= \sqrt{70(70-62.4)(70-43.5)(70-34.1)}\\ Area&= \sqrt{506,118.2}\\ Area&\approx 711.4 \end{align*}\]
The developer has about \(711.4\) square meters.
Exercise \(\PageIndex{4}\)
Find the area of a triangle given \(a=4.38\) ft , \(b=3.79\) ft, and \(c=5.22\) ft.
- Answer
-
about \(8.15\) square feet
Media
Access these online resources for additional instruction and practice with the Law of Cosines.
Key Equations
| Law of Cosines |
\(a^2=b^2+c^2−2bc \cos \alpha\) \(b^2=a^2+c^2−2ac \cos \beta\) \(c^2=a^2+b^2−2ab \cos \gamma\) |
| Heron’s formula |
\(Area=\sqrt{s(s−a)(s−b)(s−c)}\) where \(s=\dfrac{(a+b+c)}{2}\) |
Key Concepts
- The Law of Cosines defines the relationship among angle measurements and lengths of sides in oblique triangles.
- The Generalized Pythagorean Theorem is the Law of Cosines for two cases of oblique triangles: SAS and SSS. Dropping an imaginary perpendicular splits the oblique triangle into two right triangles or forms one right triangle, which allows sides to be related and measurements to be calculated. See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\).
- The Law of Cosines is useful for many types of applied problems. The first step in solving such problems is generally to draw a sketch of the problem presented. If the information given fits one of the three models (the three equations), then apply the Law of Cosines to find a solution. See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- Heron’s formula allows the calculation of area in oblique triangles. All three sides must be known to apply Heron’s formula. See Example \(\PageIndex{5}\) and See Example \(\PageIndex{6}\).
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


