3.4: Cosets and Lagrage's Theorem
- Page ID
- 694
In this section, we'll prove Lagrange's Theorem, a very beautiful statement about the size of the subgroups of a finite group. But to do so,we'll need to learn about cosets.
Recall the Cayley graph for the dihedral group \(D_5\) as generated by a flip and a rotation. Notice that the darker blue arrows look like two different 'copies' of \(\mathbb{Z}_5\) sitting inside of the dihedral group. Likewise, the light arrow loops look like five copies of \(\mathbb{Z}_2\). Both \(\mathbb{Z}_5\) and \(\mathbb{Z}_2\) are subgroups of \(D_5\), generated by the rotation and flip respectively. These 'copies' of the subgroups that we see in the Cayley graph are examples of cosets.
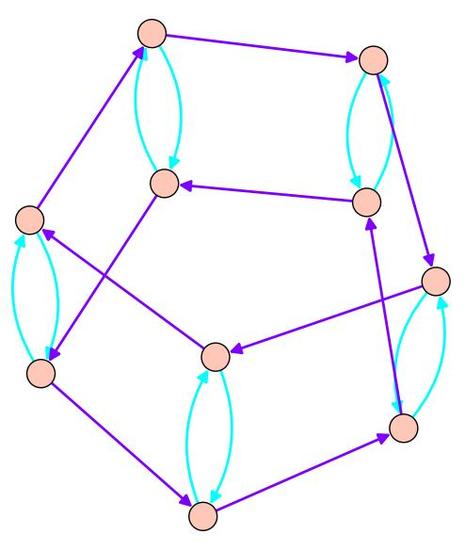
Dihedral group Cayley graph, generated by a flip and rotation. The Cayley graph for the dihedral group with generators given by a flip and a rotation.
Let \(H\) be a subgroup of \(G\), and \(H=\{h_1, h_2, h_3, \ldots \}\). Then for any choice of \(g\in G\), the coset \(gH\) is the set \(\{gh_1, gh_2, \ldots \} \).
These are precisely the 'copies' of the subgroups that we saw in \(D_5\). The elements of \(D_5\) can all be written as \(f^ir^j\) with \(i\in \{0,1\}\) and \(j\in \{0,1,\ldots,4\}\). The rotation subgroup consists of the element \(R=\{e, r, r^2, r^3, r^4\}\). Then \(R\) has two distinct cosets, \(R\) and \(fR=\{f, fr, fr^2, fr^3, fr^4\}\). For any \(g\) we choose, \(gR\) is equal to one of these two cosets! Likewise, if we consider the subgroup \(F=\{e, f\}\), there are five distinct cosets given by \(r^iF\), where \(i\in \{0,1,2,3,4\}\). Notice that the cosets evenly divide up the group; this isn't an accident!
| Proposition 3.3.1 |
|---|
| Suppose that \(H\) is a subgroup of \(G\). Let \(x, y\in G\). Then either \(xH=yH\) or \(xH\) and \(yH\) have no elements in common. |
| Proof 3.3.2 |
|---|
| Suppose \(z\in xH\) and \(z\in yH\). In particular, there exist \(h_1, h_2\in H\) such that \(z=xh_1=yh_2\), and \(xh_1h_2^{-1}=y\). We need to show that \(xH=yH\), so take any \(h_3\in H\) and consider \(yh_3\in yH\). Then \(yh_3=xh_1h_2^{-1}h_3\in xH\), since \(h_1h_2^{-1}h_3\in H\). Thus, if \(xH\) and \(yH\) share any elements, then they are equal, and if they share no elements, they are tautologically disjoint! |
We'll need one more piece of notation.
The order of a group \(G\), written \(|G|\), is the number of elements in \(G\).
So the order of \(R\subset D_5\) is \(|R|=5\), and the order of the flip subgroup \(|F|=2\). We can now prove Lagrange's Theorem!
| Theorem 3.3.4: Lagrange's Theorem |
|---|
| Let \(H\) be a subgroup of a finite group \(G\). Then \(|H|\) divides \(|G|\). |
| Proof 3.3.5: Lagrange's Theorem |
|---|
| Notice that every element of the group \(G\) shows up in some coset of \(H\): since \(e\in H\), we have \(g\in gH\) for every \(g\). Therefore, every element of the group shows up in exactly one coset of \(H\). Also notice that every coset of \(H\) has the same number of elements as \(H\). (If the size of \(gH\) were less than \(|H|\), there would be have to be two different elements \(h_1, h_2\in H\) with \(gh_1=gh_2\). But cancelling the \(g\)'s gives \(h_1=h_2\), a contradiction.) Then the cosets of \(H\) break up \(G\) evenly into subsets of size \(|H|\). Thus, \(|H|\) divides \(|G|\), as desired. |
Find all of the subgroups of the permutation group \(S_3\) and the dihedral group \(D_5\).
Find a subgroup of the permutation group \(S_4\) with twelve elements. What are it's cosets?
Contributors and Attributions
- Tom Denton (Fields Institute/York University in Toronto)


