2.1: Symmetry and Functions
- Page ID
- 682
(For best results, view this video in full-screen.)
Now we will work towards a precise definition of a group. In mathematics, we often begin explorations with some general concept (in our case, symmetry) and then work on those concepts until we can arrive at a very precise definition. Having precise definitions allows us better abstractions and generalizations; the more precise our definitions, the better the mathematics we can expect to derive.
Recall our definition of the symmetries of a geometric object: all of the ways of moving that object back onto itself without changing it. Each of these different ways of moving the object back onto itself we can identify as a function. Let's call our object \(X\). Then every symmetry of \(X\) we can identify as a certain special function \(f:X\rightarrow X\).
Earlier we noted that leaving \(X\) alone should also be a symmetry of \(X\). This is the identity function! \(id:X\rightarrow X\), with \(id(x)=x\) for all points \(x\in X\).
Next, we notice that composition of functions is a helpful operation: Indeed, if we have two different symmetries \(f\) and \(g\) of \(X\), then their composition \(g\circ f\) will also be a symmetry. The first function applied to \(X\) 'moves \(X\) onto itself without changing it,' and then the second does as well. Thus, the composition is also a symmetry.
Finally, we note in passing that the composition of functions is associative: for three symmetries \(f,g,h\), we have \((f\circ g)\circ h = f\circ (g\circ h)\).
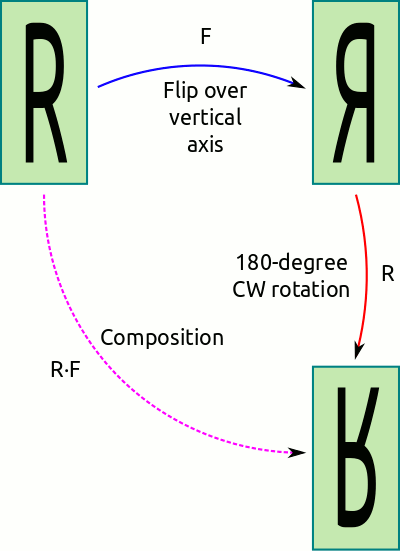
Composition of two symmetries of a rectangle.
We really need some examples here! So let's consider the perfectly symmetrical face. There are only two symmetries: the identity and the left-to-right flip (reflection over the vertical axis). Call the identity \(e\) and the flip \(f\). Then we see that, considered as functions from the face to itself, \(f\circ f=e\).
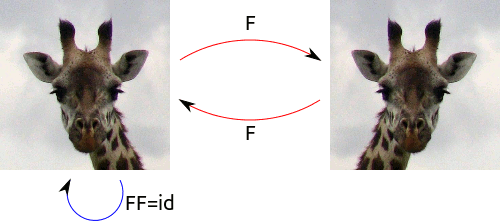
The red arrows describe the flip over the vertical axis. Do it twice, and you end up where you started: \(F\circ F=id\).
Now remember our 'bumpy' hexagon, which only had rotational symmetries. Call the identity \(e\) and let \(r\) be the clockwise rotation by \(60^\circ\). All of the other rotations we can think of as \(r\) composed with itself some number of times; we'll just write this as \(r^k\). So all of the symmetries of the bumpy hexagon are \(\{e, r, r^2, r^3, r^4, r^5\}\). We notice that \(r^5\circ r=r^6=e\). This is quite interesting! In fact, we can make a 'composition table' to keep track of what happens when we compose any two of the symmetries.
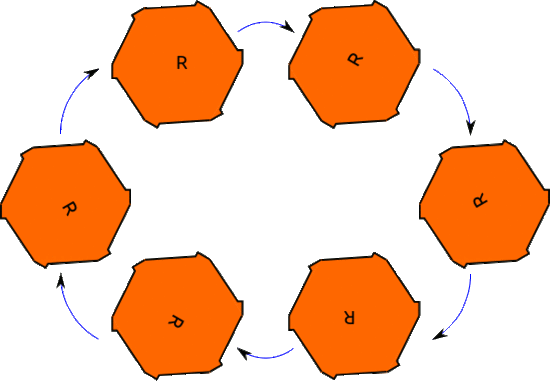
The six rotational symmetries of the bumpy hexagon. The blue arrow represents the rotation \(r\); \(r^6=id\).
And now we can make a slightly less obvious observation: For any of these functions, we can find another symmetry taking the object 'back' to its original orientation. Thus, for any symmetry \(f\), there exists a \(g\) such that \(f\circ g=e\). The function \(g\) is then called the inverse of \(f\). We've already seen two examples of this.


