6.1: Group Actions
- Page ID
- 700
Group actions bring us back to our original view of groups as measures of symmetry. We begin with a definition.
Let \(G\) be a group. A set \(S\) is a (left) \(G\)-set if there is a function from \(G\times S\rightarrow S\) (which we will write as \(g\cdot s\) for \(g\in G, s\in S\)) satisfying:
- \((gh)\cdot s = g\cdot (h\cdot s)\) for all \(g, h\in G, s\in S\), and
- \(1\cdot s=s\) for all \(s\in S\).
An analogous definition can be written for a right \(G\)-set; a right \(G\)-set has a function from \(S\times G\rightarrow S\).
These conditions say, in plain language, that elements of \(G\) move objects in the set to other objects, in a way which respects the group operation. (ie, it doesn't matter whether you perform the operation before or after applying the action.) Furthermore, the identity fixes every element of the set.
It's best to start with some easy combinatorial examples.
- Let \(G\) be a group and \(S\) be any set. The trivial action of \(G\) on \(S\) is given by \(g\cdot s=s\) for every \(g\in G, s\in S\). One can easily check that the conditions for a group action hold!
- Consider \(S_n\) and a set \(S\) of \(n\) labelled objects. Then the permutations of the objects constitute an action of \(S_n\) on \(S\).
- But \(S_n\) can also act on sets with more than \(n\) elements! Consider a regular deck of playing cards; each card has one of four suits (Clubs, Spades, Hearts, or Diamonds) and are numbered \(1\) to \(13\). (Where a Jack is \(11\), Queen is \(12\) and King is \(13\).) We can write each card in a short form: \(4D\) is short for 'four of diamonds.' Then \(S_4\) acts on the deck of cards by permuting the suits of the cards. For example, consider the permutation \(\sigma\) which transposes hearts and diamonds while leaving clubs and spades alone. Then \(\sigma(4D)=4H\), and \(\sigma(12C)=12C\).
On the other hand, \(S_{13}\) acts on the values of the cards while leaving the suits alone. For convenience, we write the action on values of cards on the right and the action on suits on the left. Let \(\tau\) be the permutation in \(S_{13}\) which sends \(i\) to \(i+1\), and \(13\) to \(1\). Then \(4D\cdot \tau=5D\). Combining the left and right actions, we have \(\sigma\cdot 4D\cdot \tau=5H\), for example.
- And \(S_n\) can act on sets with fewer than \(n\) elements. Consider a coin, with a 'heads' side (\(H\)) and a 'tails' side (\(T\)). We can define an action of \(S_n\) where \(\sigma\) flips the coin if the sign of \(\sigma\) is negative, and leaves the coin alone if the sign of \(\sigma\) is positive. Here the set we're acting on is actually the set of states of the coin: \(\{H, T\}\).
Just as we made Cayley graphs of groups, we can also make Cayley graphs of group actions. If our group \(G\) has a generating set \(\{g_1, g_2, \ldots, g_k\}\), then the Cayley graph has one vertex for each element of the set \(S\) and colored edges from each \(s\) to \(g_i\cdot s\).
For the example of \(S_n\) acting on a coin, the Cayley graph will just have two vertices, \(H\) and \(T\), and arrows according to the action of the generators. If we consider the generating set of simple transpositions (which, we'll recall, exchange \(i\) and \(i+1\) and leave everything else alone), the Cayley graph will have arrows from \(H\) to \(T\) and back for each simple transposition. (Because all simple transpositions have sign \(-1\).)

Figure 6.1: Cayley graph for action of \(S_4\) on a coin, with generators given by the simple transpositions.
Let's build a Cayley graph for the cards, but with a smaller set of cards to make things easier to draw. Imagine our deck only has two suits - Spades and Diamonds - and only numbers \(1\) through \(4\). Then let \(S_4\) act on the left by permuting numbers. The Cayley graph is below.
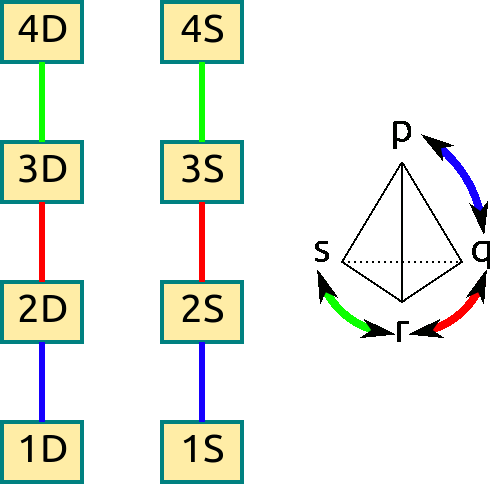
Figure 6.2: Cayley diagram for \(S_4\) acting on some cards numbered \(1\) through \(4\), whose suits are all either diamonds (D) or spades (S).
Notice that the action is broken up into two different connected pieces: Exchanging numbers will never allow us to change suits, but we can switch around numbers freely. As a result, the suits each form a 'block' from which the other blocks can't be reached. These blocks are called orbits; we'll study them intensively in the next section.
Contributors and Attributions
- Tom Denton (Fields Institute/York University in Toronto)


