3.5: Matrices and Gaussian Elimination

Last updated
Save as PDF

Page ID: 6244

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Use back substitution to solve linear systems in upper triangular form.
Convert linear systems to equivalent augmented matrices.
Use matrices and Gaussian elimination to solve linear systems.

Back Substitution

Recall that a linear system of equations consists of a set of two or more linear equations with the same variables. A linear system consisting of three equations in standard form arranged so that the variable $x$ does not appear in any equation after the first and the variable $y$ does not appear in any equation after the second is said to be in upper triangular form²². For example,

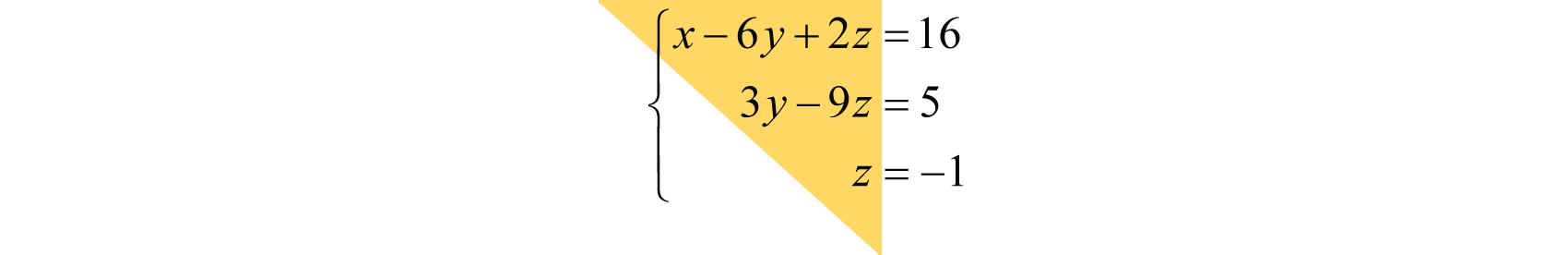
Notice that the system forms a triangle where each successive equation contains one less variable. In general,

$\color{Cerulean}{Linear\: Systems\: in\: Upper\: Triangular\: Form}$

$\left\{ \begin{array} { r l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { b _ { 2 } y = c _ { 2 } }\end{array} \right. \quad\quad\left\{ \begin{array} { r l } { a _ { 1 } x + b _ { 1 } y + c_{1}z= d _ { 1 } } \\ { b _ { 2 } y + c_{2}z = d _ { 2 }\\ \\\quad\quad\:\:\: c_{3}z = d_{3} }\end{array} \right.$

If a linear system is in this form, we can easily solve for one of the variables and then back substitute to solve for the remaining variables.

Example $\PageIndex{1}$:

Solve: $\left\{ \begin{aligned} 3 x - y & = 7 \\ 2 y & = - 2 \end{aligned} \right.$

Solution

Recall that solutions to linear systems with two variables, if they exist, are ordered pairs $(x, y)$. We can determine the $y$-value easily using the second equation.

$\begin{aligned} 2 y & = - 2 \\ y & = - 1 \end{aligned}$

Next, use the first equation $3x − y = 7$ and the fact that $y = −1$ to find $x$.

$\begin{aligned} 3 x - y & = 7 \\ 3 x - ( \color{Cerulean}{- 1}\color{black}{ )} & = 7 \\ 3 x + 1 & = 7 \\ 3 x & = 6 \\ x & = 2 \end{aligned}$

Answer:

$(2, -1)$

Example $\PageIndex{2}$:

Solve: $\left\{ \begin{aligned} x - 6 y + 2 z & = 16 \\ 3 y - 9 z & = 5 \\ z & = - 1 \end{aligned} \right.$.

Solution

Recall that solutions to linear systems with three variables, if they exist, are ordered triples $(x, y, z)$. Use the second equation $3y − 9z = 5$ and the fact that $z = −1$ to find $y$.

$\begin{aligned} 3 y - 9 z & = 5 \\ 3 y - 9 (\color{Cerulean}{ - 1}\color{black}{ )} & = 5 \\ 3 y + 9 & = 5 \\ 3 y & = - 4 \\ y & = - \frac { 4 } { 3 } \end{aligned}$

Next substitute $y$ and $z$ into the first equation.

$\begin{aligned} x - 6 y + 2 z & = 16 \\ x - 6 \left( \color{Cerulean}{- \frac { 4 } { 3} } \right) + 2 ( \color{Cerulean}{- 1}\color{black}{ )} & = 16 \\ x + 8 - 2 & = 16 \\ x + 6 & = 16 \\ x & = 10 \end{aligned}$

Answer:

$(10, -\frac{4}{3}, -1)$

Exercise $\PageIndex{1}$

Solve: $\left\{ \begin{aligned} 4 x - y + 3 z & = 1 \\ 2 y - 9 z & = - 2 \\ 3 z & = 2 \end{aligned} \right.$

Answer

$\left( \frac { 1 } { 4 } , 2 , \frac { 2 } { 3 } \right)$

www.youtube.com/v/RBUxjSq-bVU

Matrices and Gaussian Elimination

In this section the goal is to develop a technique that streamlines the process of solving linear systems. We begin by defining a matrix²³, which is a rectangular array of numbers consisting of rows and columns. Given a linear system in standard form, we create a coefficient matrix²⁴ by writing the coefficients as they appear lined up without the variables or operations as follows.

$\quad\quad\quad\quad\quad\color{Cerulean}{Linear\:System} \quad\quad\quad\quad\quad\color{Cerulean}{Coefficient\:Matrix} \\\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right. \quad \quad\Rightarrow\quad \quad \left[ \begin{array} { l } { a _ { 1 } b _ { 1 } c _ { 1 } } \\ { a _ { 2 } b _ { 2 } c _ { 2 } } \\ { a _ { 3 } b _ { 3 } c _ { 3 } } \end{array} \right]$

The rows represent the coefficients in the equations and the columns represent the coefficients of each variable. Furthermore, if we include a column that represents the constants we obtain what is called an augmented matrix²⁵. For a linear system with two variables,

$\quad\quad\quad\quad\color{Cerulean}{Linear\:System}\quad\color{Cerulean}\quad\quad{Augmented\:Matrix} \\\left\{ \begin{array} { l l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y = c _ { 2 } } \end{array} \right.\quad\quad \Leftrightarrow \quad\quad \left[ \begin{array} { l } { a _ { 1 } b _ { 1 } \left| c _ { 1 } \right. } \\ { a _ { 2 } b _ { 2 } \left| c _ { 2 } \right. } \end{array} \right]$

And for a linear system with three variables we have

$\quad\quad\quad\quad\color{Cerulean}{Linear\:System}\quad\color{Cerulean}\quad\quad{Augmented\:Matrix} \\\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right.\quad\quad \Leftrightarrow \quad\left[ \begin{array} { l } { a _ { 1 } b _ { 1 } c _ { 1 } \left| d _ { 1 } \right. } \\ { a _ { 2 } b _ { 2 } c _ { 2 } \left| d _ { 2 } \right. } \\ { a _ { 3 } b _ { 3 } c _ { 3 } \left| d _ { 3 } \right. } \end{array} \right]$

Note

The dashed vertical line provides visual separation between the coefficient matrix and the column of constants. In other algebra resources that you may encounter, this is sometimes omitted.

Example $\PageIndex{3}$:

Construct the augmented matrix that corresponds to: $\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right.$.

Solution

This system consists of two linear equations in standard form; therefore, the coefficients in the matrix appear as they do in the system.

$\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c } { 9 } & { - 6}&{0 } \\ { - 1 } &{ 2} &{ 1} \end{array} \right]$

Example $\PageIndex{4}$:

Construct the augmented matrix that corresponds to: $\left\{ \begin{aligned} x + 2 y - 4 z & = 5 \\ 2 x + y - 6 z & = 8 \\ 4 x - y - 12 z & = 13 \end{aligned} \right.$

Solution

Since the equations are given in standard form, the coefficients appear in the matrix as they do in the system.

$\left\{ \begin{array} { c c } { x + 2 y - 4 z = 5 } \\ { 2 x + y - 6 z = 8 } \\ { 4 x - y - 12 z = 13 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c c | c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 2 } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]$

A matrix is in upper triangular form if all elements below the leading nonzero element in each successive row are zero. For example,

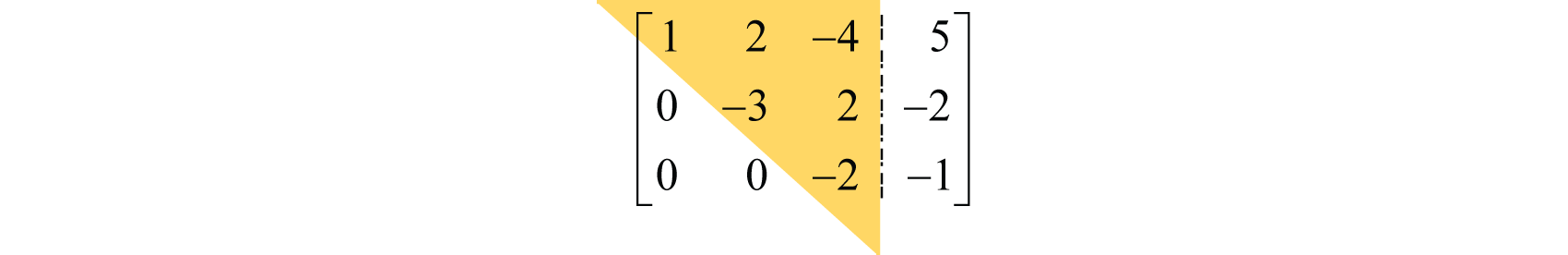
Notice that the elements below the main diagonal are zero and the coefficients above form a triangular shape. In general,

$\color{Cerulean}{Upper\:Triangular\:Form}\\\left[ \begin{array} { c c } { a _ { 1 }} & { b _ { 1 } } \\ { 0} &{ b _ { 2 } } \end{array} \right] \quad \left[ \begin{array} { c c c } { a _ { 1 }} &{ b _ { 1 }} & { c _ { 1 } } \\ { 0} &{ b _ { 2 }}&{ c _ { 2 } } \\ { 0 } & { 0} &{ c _ { 3 } } \end{array} \right]$

This is important because in this section we outline a process by which certain operations can be made to produce an equivalent linear system in upper triangular form so that it can be solved by using back substitution. An overview of the process is outlined below:

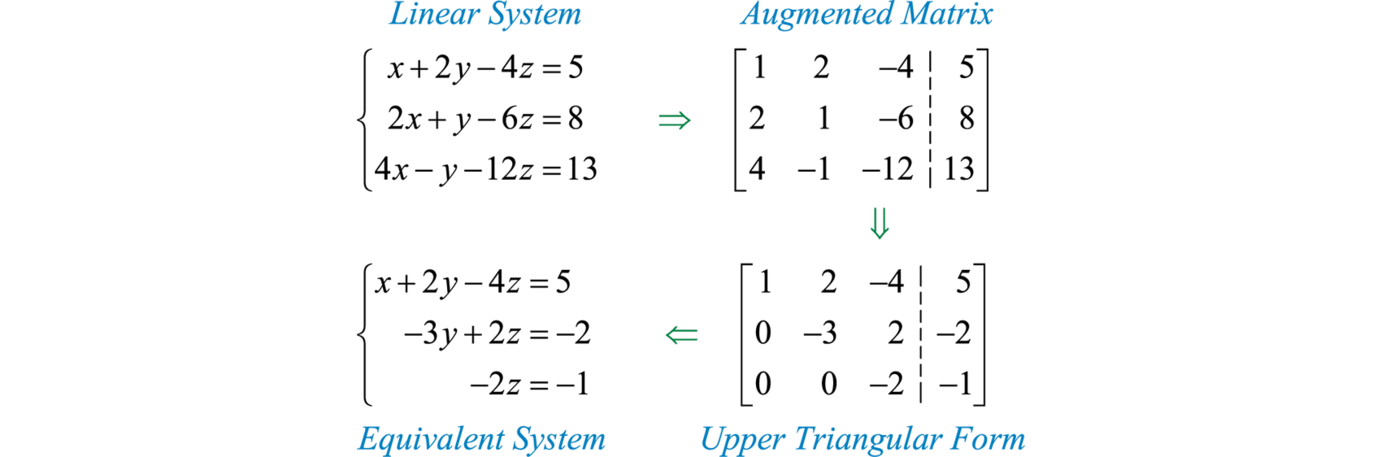
Once the system is in upper triangular form, we can use back substitution to easily solve it. It is important to note that the augmented matrices presented here represent linear systems of equations in standard form.

The following elementary row operations²⁶ result in augmented matrices that represent equivalent linear systems:

Any two rows may be interchanged.
Each element in a row can be multiplied by a nonzero constant.
Any row can be replaced by the sum of that row and a multiple of another.

Note

These operations are consistent with the properties used in the elimination method.

To efficiently solve a system of linear equations first construct an augmented matrix. Then apply the appropriate elementary row operations to obtain an augmented matrix in upper triangular form. In this form, the equivalent linear system can easily be solved using back substitution. This process is called Gaussian elimination²⁷, named in honor of Carl Friedrich Gauss (1777–1855).

$ec7ac4a7fc8f6e2b81852d96c636be9a.png$
Figure $\PageIndex{4}$: Carl Friedrich Gauss

The steps for solving a linear equation with two variables using Gaussian elimination are listed in the following example.

Example $\PageIndex{5}$:

Solve using matrices and Gaussian elimination: $\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right.$.

Solution

Ensure that the equations in the system are in standard form before beginning this process.

Step 1: Construct the corresponding augmented matrix.

$\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c} { 9} &{ - 6} & {0 } \\ { - 1} &{2}&{1 } \end{array} \right]$

Step 2: : Apply the elementary row operations to obtain upper triangular form. In this case, we need only to eliminate the first element of the second row, $−1$. To do this, multiply the second row by $9$ and add it to the first row.

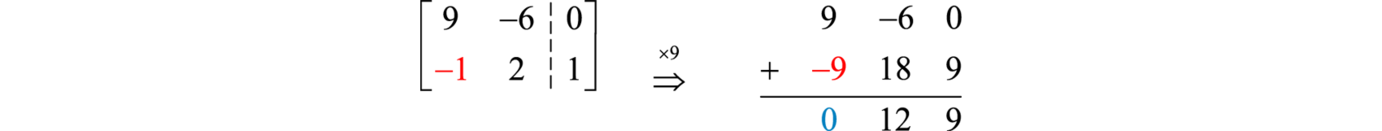
Now use this to replace the second row.

$\left[ \begin{array} { c c | c } { 9 } & { - 6}&{0 } \\ {\color{Cerulean}{ 0} } & { \color{black}{12} } & { 19 } \end{array} \right]$

This results in an augmented matrix in upper triangular form.

Step 3: Convert back to a linear system and solve using back substitution. In this example, we have

$\left[ \begin{array} { c c |c} { 9} &{ - 6} &{0 } \\ { \color{Cerulean}{0} } & { \color{black}{12}} &{ 9 } \end{array} \right] \Rightarrow \left\{ \begin{array} { r } { 9 x - 6 y = 0 } \\ { 12 y = 9 } \end{array} \right.$

Solve the second equation for $y$,

$\begin{array} { l } { 12 y = 9 } \\ { y = \frac { 9 } { 12 } } \\ { y = \frac { 3 } { 4 } } \end{array}$

Substitute this value for $y$ into the first equation to find $x$,

$\begin{aligned} 9 x - 6 y & = 0 \\ 9 x - 6 \left( \color{OliveGreen}{\frac { 3 } { 4 }} \right) & = 0 \\ 9 x - \frac { 9 } { 2 } & = 0 \\ 9 x & = \frac { 9 } { 2 } \\ x & = \frac { 1 } { 2 } \end{aligned}$

Answer:

$\left( \frac { 1 } { 2 } , \frac { 3 } { 4 } \right)$

The steps for using Gaussian elimination to solve a linear equation with three variables are listed in the following example.

Example $\PageIndex{6}$:

Solve using matrices and Gaussian elimination: $\left\{ \begin{array} { c } { x + 2 y - 4 z = 5 } \\ { 2 x + y - 6 z = 8 } \\ { 4 x - y - 12 z = 13 } \end{array} \right.$

Solution

Ensure that the equations in the system are in standard form before beginning this process.

Step 1: Construct the corresponding augmented matrix.

$\left\{ \begin{array} { c c c } { x + 2 y - 4 z } & { = 5 } \\ { 2 x + y - 6 z } & { = 8 } \\ { 4 x - y - 12 z } & { = 13 } \end{array} \right.\quad \color{Cerulean}{\Rightarrow} \color{black}{\quad \left[ \begin{array} { c c c | c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 2 } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]}$

Step 2: Apply the elementary row operations to obtain upper triangular form. We begin by eliminating the first element of the second row, $2$ in this case. To do this multiply the first row by $−2$ and then add it to the second row.

$ \left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{red}{2} } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right] \stackrel{\stackrel {\times( - 2 )}{\Longrightarrow}}{}\begin{array} { c c c c }\:\;\:\:\:\: { - 2} &{ - 4} &\:\:{ 8} &{ - 10 } \\ + \:\:\:\:\:\:{ \color{red}{2}} & {\color{black}{1}} & {- 6} &{8 } \\ \hline \:\:\:\:\:\:\:\: {\color{Cerulean}{0}} &{ - 3} & {2} & { - 2 } \end{array}$

Use this to replace the second row.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{Cerulean}{0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]$

Next, eliminate the first element of the third row, $4$ in this case, by multiplying the first row by $−4$ and adding it to the third row.

$ \left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 0 } & { -3 } & { 2 } & { -2 } \\ { \color{red}{4} } & { \color{black}{- 1} } & { - 12 } & { 13 } \end{array} \right] \stackrel{\stackrel {\times( - 4 )}{\Longrightarrow}}{}\begin{array} { c c c c }\:\;\:\:\:\: { - 4} &{ - 8} &{ 16} &{ - 20 } \\ + \:\:\:\:\:\:{ \color{red}{4}} & {\color{black}{-1}} & {- 12} &{13 } \\ \hline \:\:\:\:\:\:\:\: {\color{Cerulean}{0}} &{ - 9} & {4} & { - 7 } \end{array}$

Use this to replace the third row.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ {\color{Cerulean}{ 0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { \color{Cerulean}{0} } & { \color{black}{- 9} } & { 4 } & { - 7 } \end{array} \right]$

This results in an augmented matrix where the elements below the first element of the first row are zero. Next eliminate the second element in the third row, in this case $−9$. Multiply the second row by $−3$ and add it to the third row.

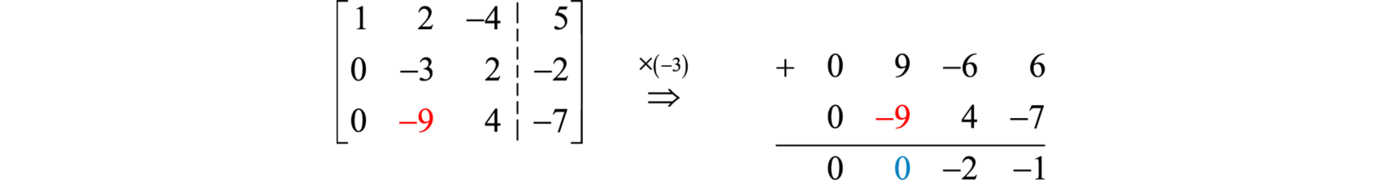
Use this to replace the third row and we can see that we have obtained a matrix in upper triangular form.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{Cerulean}{0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { \color{Cerulean}{0} } & { \color{Cerulean}{0} } & {\color{black}{ - 2} } & { - 1 } \end{array} \right]$

Step 3: Convert back to a linear system and solve using back substitution. In this example, we have

$\left[ \begin{array} { c c c |c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 0 } & { - 3 } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { - 2 } & { - 1 } \end{array} \right] \Rightarrow \left\{ \begin{array} { r } { x + 2 y - 4 z = 5 } \\ { - 3 y + 2 z = - 2 } \\ { - 2 z = - 1 } \end{array} \right.$

Answer:

It is left to the reader to verify that the solution is $(5, 1, \frac{1}{2})$.

Note

Typically, the work involved in replacing a row by multiplying and adding is done on the side using scratch paper.

Example $\PageIndex{7}$:

Solve using matrices and Gaussian elimination: $\left\{ \begin{aligned} 2 x - 9 y + 3 z &= - 18 \\ x - 2 y - 3 z &= - 8 \\ - 4 x + 23 y + 12 z &= 47 \end{aligned} \right.$

Solution

We begin by converting the system to an augmented coefficient matrix.

$\left\{ \begin{aligned} 2 x - 9 y + 3 z &= - 18 \\ x - 2 y - 3 z& = - 8 \\ - 4 x + 23 y + 12 z &= 47 \end{aligned} \right. \color{OliveGreen}{\Rightarrow} \color{black}{\left[ \begin{array} { c c c | c } { 2 }&{- 9 } & { 3} &{ - 18 } \\ { 1} &{ - 2 } & { - 3 } & { - 8 } \\ { - 4 } & { 23 } & { 12 } & { 47 } \end{array} \right]}$

The elementary row operations are streamlined if the leading nonzero element in a row is $1$. For this reason, begin by interchanging row one and two.

Replace row two with the sum of $−2$ times row one and row two.

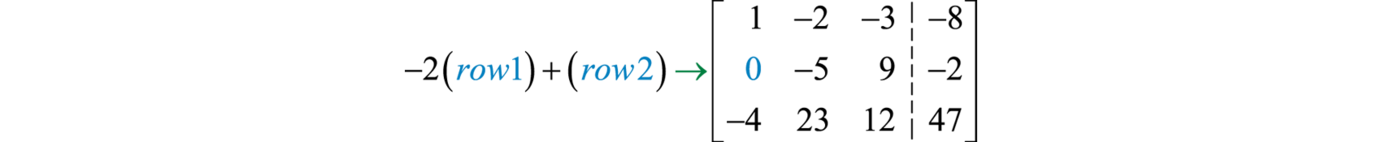
Replace row three with the sum of $4$ times row one and row three.

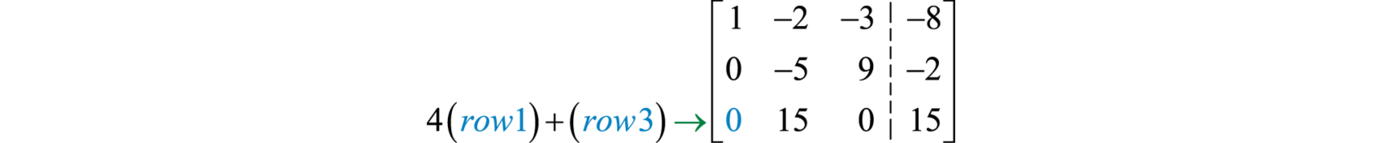
Next divide row $3$ by $15$.

Interchange row three with row two.

Next replace row $3$ with the sum of $5$ times row two and row three.

This results in a matrix in upper triangular form. A matrix is in row echelon form²⁸ if it is in upper triangular form where the leading nonzero element of each row is $1$. We can obtain this form by replacing row three with the results of dividing it by $9$.

Convert to a system of linear equations and solve by back substitution.

$\left[ \begin{array} { c c c | c} { 1} &{ - 2} &{ - 3} &{ - 8 } \\ { 0 } & { 1 } & { 0 } & { 1 } \\ { 0 } & { 0 } & { 1 } & { \frac { 1 } { 3 } } \end{array} \right] \Rightarrow \left\{ \begin{aligned} x - 2 y - 3 z & = - 8 \\ y & = 1 \\ z & = \frac { 1 } { 3 } \end{aligned} \right.$

Here $y = 1$ and $z = \frac{1}{3}$. Substitute into the first equation to find $x$.

$\begin{aligned} x - 2 y - 3 y & = - 8 \\ x - 2 ( \color{Cerulean}{1}\color{black}{ )} - 3 \left(\color{Cerulean}{ \frac { 1 } { 3} } \right) & = - 8 \\ x - 2 - 1 & = - 8 \\ x - 3 & = - 8 \\ x & = - 5 \end{aligned}$

Answer:

Therefore the solution is $\left( - 5,1 , \frac { 1 } { 3 } \right)$.

Note

Many modern calculators and computer algebra systems can perform Gaussian elimination. First you will need to find out how to enter a matrix. Then use the calculator’s functions to find row echelon form. You are encouraged to conduct some web research on this topic for your particular calculator model.

Exercise $\PageIndex{2}$

Solve using Gaussian elimination: $\left\{ \begin{array} { c } { x - 3 y + 2 z = 16 } \\ { 4 x - 11 y - z = 69 } \\ { 2 x - 5 y - 4 z = 36 } \end{array} \right.$.

Answer

$( 6 , - 4 , - 1 )$

www.youtube.com/v/8mavvyGOedM

Example $\PageIndex{8}$:

Solve using matrices and Gaussian elimination: $\left\{ \begin{array} { c } { x - 2 y + z = 4 } \\ { 2 x - 3 y + 4 z = 7 } \\ { 4 x - 7 y + 6 z = 15 } \end{array} \right.$.

Solution

We begin by converting the system to an augmented coefficient matrix.

$\left\{ \begin{array} { c c } { x - 2 y + z = 4 } \\ { 2 x - 3 y + 4 z = 7 } \\ { 4 x - 7 y + 6 z = 15 } \end{array} \right. \color{OliveGreen}{\Rightarrow} \color{black}{ \left[ \begin{array} { c c | c } { 1} &{ - 21} &{ 4 } \\ { 2} &{ - 34}&{ 7 } \\ { 4} &{ - 76}&{ 15 } \end{array} \right]}$

Replace row two with $−2$ (row $1$) + (row $2$)and replace row three with $−4$ (row $1$) + (row $3$).

$\left[ \begin{array} { c c |c } { 1 } & { - 21 } & { 4 } \\ { 0 } & { 12 } & { - 1 } \\ { 0 } & { 12 } & { - 1 } \end{array} \right]$

Replace row three with $−1$ (row $2$) + (row $3$).

$\left[ \begin{array} { c c | c} { 1 } & { - 21 } & { 4 } \\ { 0 } & { 12 } & { - 1 } \\ { 0 } & { 00 } & { 0 } \end{array} \right]$

The last row indicates that this is a dependent system because converting the augmented matrix back to equations we have,

$\left\{ \begin{aligned} x - 2 y + z & = 4 \\ y + 2 z & = - 1 \\ 0 x + 0 y + 0 z & = 0 \end{aligned} \right.$

Note that the row of zeros corresponds to the following identity,

$\begin{array} { r } { 0 x + 0 y + 0 z = 0 } \\ { 0 = 0 } \end{array} \color{Cerulean}{✓}$

In this case, we can express the infinitely many solutions in terms of $z$. From the second row we have the following:

$\begin{aligned} y + 2 z & = - 1 \\ y & = - 2 z - 1 \end{aligned}$

And from the first equation,

$\begin{aligned} x - 2 y + z & = 4 \\ x - 2 ( \color{Cerulean}{- 2 z - 1}\color{black}{ )} + z & = 4 \\ x + 5 z + 2 & = 4 \\ x & = - 5 z + 2 \end{aligned}$

The solutions take the form $(x, y, z) = (−5z + 2, −2z − 1, z)$ where $z$ is any real number.

Answer:

$( - 5 z + 2 , - 2 z - 1 , z )$

Dependent and inconsistent systems can be identified in an augmented coefficient matrix when the coefficients in one row are all zero.

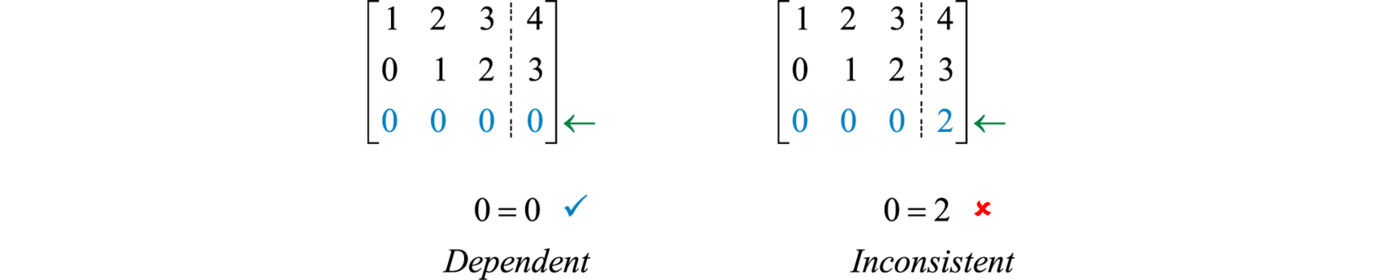
If a row of zeros has a corresponding constant of zero then the matrix represents a dependent system. If the constant is nonzero then the matrix represents an inconsistent system.

Exercise $\PageIndex{3}$

Solve using matrices and Gaussian elimination: $\left\{ \begin{aligned} 5 x - 2 y + z & = - 3 \\ 10 x - y + 3 z & = 0 \\ - 15 x + 9 y - 2 z & = 17 \end{aligned} \right.$.

Answer

$\varnothing$

www.youtube.com/v/38W0EB5e0pY

Key Takeaways

A linear system in upper triangular form can easily be solved using back substitution.
The augmented coefficient matrix and Gaussian elimination can be used to streamline the process of solving linear systems.
To solve a system using matrices and Gaussian elimination, first use the coefficients to create an augmented matrix. Apply the elementary row operations as a means to obtain a matrix in upper triangular form. Convert the matrix back to an equivalent linear system and solve it using back substitution.

Exercise $\PageIndex{4}$

Solve using back substitution.

$\left\{ \begin{aligned} 5 x - 3 y & = 2 \\ y & = - 1 \end{aligned} \right.$
$\left\{ \begin{array} { r } { 3 x + 2 y = 1 } \\ { y = 3 } \end{array} \right.$
$\left\{ \begin{aligned} x - 4 y & = 1 \\ 2 y & = - 3 \end{aligned} \right.$
$\left\{ \begin{aligned} x - 5 y & = 3 \\ 10 y & = - 6 \end{aligned} \right.$
$\left\{ \begin{aligned} 4 x - 3 y & = - 16 \\ 7 y & = 0 \end{aligned} \right.$
$\left\{ \begin{aligned} 3 x - 5 y & = - 10 \\ 4 y & = 8 \end{aligned} \right.$
$\left\{ \begin{aligned} 2 x + 3 y & = - 1 \\ 3 y & = 2 \end{aligned} \right.$
$\left\{ \begin{aligned} 6 x - y & = - 3 \\ 4 y & = 3 \end{aligned} \right.$
$\left\{ \begin{aligned} x - y & = 0 \\ 2 y & = 0 \end{aligned} \right.$
$\left\{ \begin{aligned} 2 x + y & = 2 \\ 3 y & = 0 \end{aligned} \right.$
$\left\{ \begin{aligned} x + 3 y - 4 z & = 1 \\ y - 3 z & = - 2 \\ z & = 3 \end{aligned} \right.$
$\left\{ \begin{aligned} x - 5 y + 4 z & = - 1 \\ y - 7 z & = 10 \\ z & = - 2 \end{aligned} \right.$
$\left\{ \begin{aligned} x - 6 y + 8 z & = 2 \\ 3 y - 4 z & = - 4 \\ 2 z & = - 1 \end{aligned} \right.$
$\left\{ \begin{aligned} 2 x - y + 3 z & = - 9 \\ 2 y + 6 z & = - 2 \\ 3 z & = 2 \end{aligned} \right.$
$\left\{ \begin{aligned} 10 x - 3 y + z & = 13 \\ 11 y - 3 z & = 9 \\ 2 z & = - 6 \end{aligned} \right.$
$\left\{ \begin{aligned} 3 x - 2 y + 5 z & = - 24 \\ 4 y + 5 z & = 3 \\ 4 z & = - 12 \end{aligned} \right.$
$\left\{ \begin{aligned} x - y + 2 z & = 1 \\ 2 y + z & = 1 \\ 3 z & = - 1 \end{aligned} \right.$
$\left\{ \begin{aligned} x + 2 y - z & = 2 \\ y - 3 z & = 1 \\ 6 z & = 1 \end{aligned} \right.$
$\left\{ \begin{aligned} x - 9 y + 5 z & = - 3 \\ 2 y & = 10 \\ 3 z & = 27 \end{aligned} \right.$
$\left\{ \begin{aligned} 4 x - z & = 3 \\ 3 y - 2 z & = - 1 \\ 2 z & = - 8 \end{aligned} \right.$

Answer

1. $\left( - \frac { 1 } { 5 } , - 1 \right)$

3. $\left( - 5 , - \frac { 3 } { 2 } \right)$

5. $(-4, 0)$

7. $\left( - \frac { 3 } { 2 } , \frac { 2 } { 3 } \right)$

9. $(0,0)$

11. $(-8, 7, 3)$

13. $\left( - 6 , - 2 , - \frac { 1 } { 2 } \right)$

15. $\left( \frac { 8 } { 5 } , 0 , - 3 \right)$

17. $\left( \frac { 7 } { 3 } , \frac { 2 } { 3 } , - \frac { 1 } { 3 } \right)$

19. $(-3, 5, 9)$

Exercise $\PageIndex{5}$

Construct the corresponding augmented matrix (do not solve).

$\left\{ \begin{array} { c } { x + 2 y = 3 } \\ { 4 x + 5 y = 6 } \end{array} \right.$
$\left\{ \begin{array} { l } { 6 x + 5 y = 4 } \\ { 3 x + 2 y = 1 } \end{array} \right.$
$\left\{ \begin{array} { l } { x - 2 y = 1 } \\ { 2 x - y = 1 } \end{array} \right.$
$\left\{ \begin{array} { c } { x - y = 2 } \\ { - x + y = - 1 } \end{array} \right.$
$\left\{ \begin{aligned} - x + 8 y & = 3 \\ 2 y & = 2 \end{aligned} \right.$
$\left\{ \begin{array} { r } { 3 x - 2 y = 4 } \\ { - y = 5 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x - 2 y + 7 z = 8 } \\ { 4 x - 5 y - 10 z = 6 } \\ { - x - 3 y + 2 z = - 1 } \end{array} \right.$
$\left\{ \begin{array} { c } { x - y - z = 0 } \\ { 2 x - y + 3 z = - 1 } \\ { - x + 4 y - 3 z = - 2 } \end{array} \right.$
$\left\{ \begin{aligned} x - 9 y + 5 z & = - 3 \\ 2 y & = 10 \\ 3 z & = 27 \end{aligned} \right.$
$\left\{ \begin{array} { c } { 4 x - z = 3 } \\ { 3 y - 2 z = - 1 } \\ { 2 z = - 8 } \end{array} \right.$
$\left\{ \begin{array} { c } { 8 x + 2 y = - 13 } \\ { - 2 y + z = 1 } \\ { 12 x - 5 z = - 18 } \end{array} \right.$
$\left\{ \begin{array} { l } { x - 3 z = 2 } \\ { y + 6 z = 4 } \\ { 2 x + 3 y = 12 } \end{array} \right.$

Answer

1. $\left[ \begin{array} { c c | c } { 1} & {2} &{ 3 } \\ { 4}&{5} &{ 6 } \end{array} \right]$

3. $\left[ \begin{array} { c c | c} { 1} &{ - 2} &{ 1 } \\ { 2} &{ - 1} &{ 1 } \end{array} \right]$

5. $\left[ \begin{array} { c c | c } { - 1} &{8} &{ 3 } \\ { 0} & {2} &{ 2 } \end{array} \right]$

7. $\left[ \begin{array} { c c c | c} { 3 } & { - 2 } & { 7 } & { 8 } \\ { 4} &{ - 5 } & { - 10 } & { 6 } \\ { - 1 } & { - 3 } & { 2 } & { - 1 } \end{array} \right]$

9. $\left[ \begin{array} { c c c | c } { 1 } & { - 9} &{5} &{ - 3 } \\ { 0 } & { 2} &{0 } & { 10 } \\ { 0 } & { 0} &{3 } & { 27 } \end{array} \right]$

11. $\left[ \begin{array} { c c c | c } { 8 } & { 2 } & { 0 } &{ - 13 } \\ { 0 } & { - 2 } & { 1 } & { 1 } \\ { 12 } & { 0 } & { - 5 } & { - 18 } \end{array} \right]$

Exercise $\PageIndex{6}$

Solve using matrices and Gaussian elimination.

$\left\{ \begin{array} { l } { x - 5 y = 2 } \\ { 2 x - y = 1 } \end{array} \right.$
$\left\{ \begin{array} { c } { x - 2 y = - 1 } \\ { x + y = 1 } \end{array} \right.$
$\left\{ \begin{array} { l } { 10 x - 7 y = 15 } \\ { - 2 x + 3 y = - 3 } \end{array} \right.$
$\left\{ \begin{array} { c } { 9 x - 10 y = 2 } \\ { 3 x + 5 y = - 1 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x + 5 y = 8 } \\ { 2 x - 3 y = 18 } \end{array} \right.$
$\left\{ \begin{array} { l } { 5 x - 3 y = - 14 } \\ { 7 x + 2 y = - 1 } \end{array} \right.$
$\left\{ \begin{array} { c } { 9 x + 15 y = 5 } \\ { 3 x + 5 y = 7 } \end{array} \right.$
$\left\{ \begin{array} { c } { 6 x - 8 y = 1 } \\ { - 3 x + 4 y = - 1 } \end{array} \right.$
$\left\{ \begin{array} { l } { x + y = 0 } \\ { x - y = 0 } \end{array} \right.$
$\left\{ \begin{array} { l } { 7 x - 3 y = 0 } \\ { 3 x - 7 y = 0 } \end{array} \right.$
$\left\{ \begin{array} { c } { 2 x - 3 y = 4 } \\ { - 10 x + 15 y = - 20 } \end{array} \right.$
$\left\{ \begin{array} { l } { 6 x - 10 y = 20 } \\ { - 3 x + 5 y = - 10 } \end{array} \right.$
$\left\{ \begin{array} { l } { x + y - 2 z = - 1 } \\ { - x + 2 y - z = 1 } \\ { x - y + z = 2 } \end{array} \right.$
$\left\{ \begin{array} { c } { x - y + z = - 2 } \\ { x + 2 y - z = 6 } \\ { - x + y - 2 z = 3 } \end{array} \right.$
$\left\{ \begin{aligned} 2 x - y + z & = 2 \\ x - y + z & = 2 \\ - 2 x + 2 y - z & = - 1 \end{aligned} \right.$
$\left\{ \begin{array} { l } { 3 x - y + 2 z = 7 } \\ { - x + 2 y + z = 6 } \\ { x + 3 y - 2 z = 1 } \end{array} \right.$
$\left\{ \begin{aligned} x - 3 y + z & = 6 \\ - x - y + 2 z & = 4 \\ 2 x + y + z & = 3 \end{aligned} \right.$
$\left\{ \begin{aligned} 4 x - y + 2 z & = 12 \\ x - 3 y + 2 z & = 7 \\ - 2 x + 3 y + 4 z & = - 16 \end{aligned} \right.$
$\left\{ \begin{array} { c } { 2 x - 4 y + 6 z = - 4 } \\ { 3 x - 2 y + 5 z = - 2 } \\ { 5 x - y + 2 z = 1 } \end{array} \right.$
$\left\{ \begin{aligned} 3 x + 6 y + 9 z & = 6 \\ 2 x - 2 y + 3 z & = 0 \\ - 3 x + 18 y - 12 z & = 5 \end{aligned} \right.$
$\left\{ \begin{array} { l } { - x + y - z = - 2 } \\ { 3 x - 2 y + 5 z = 1 } \\ { 3 x - 5 y - z = 3 } \end{array} \right.$
$\left\{ \begin{array} { c } { x + 2 y + 3 z = 4 } \\ { 3 x + 8 y + 13 z = 21 } \\ { 2 x + 5 y + 8 z = 16 } \end{array} \right.$
$\left\{ \begin{array} { c } { 2 x - 4 y - 5 z = 3 } \\ { - x + y + z = 1 } \\ { 3 x - 4 y - 5 z = - 4 } \end{array} \right.$
$\left\{ \begin{array} { l } { 5 x - 3 y - 2 z = 4 } \\ { 3 x - 6 y + 4 z = - 6 } \\ { - x + 2 y - z = 2 } \end{array} \right.$
$\left\{ \begin{array} { c } { - 2 x - 3 y + 12 z = 4 } \\ { 4 x - 5 y - 10 z = - 1 } \\ { - x - 3 y + 2 z = 0 } \end{array} \right.$
$\left\{ \begin{array} { c } { 3 x - 2 y + 5 z = 10 } \\ { 4 x + 3 y - 3 z = - 6 } \\ { x + y + z = 2 } \end{array} \right.$
$\left\{ \begin{array} { c } { x + 2 y + z = - 3 } \\ { x + 6 y + 3 z = 7 } \\ { x + 4 y + 2 z = 2 } \end{array} \right.$
$\left\{ \begin{array} { c } { 2 x - y + z = 1 } \\ { 4 x - y + 3 z = 5 } \\ { 2 x + y + 3 z = 7 } \end{array} \right.$
$\left\{ \begin{array} { l } { 2 x + 3 y - 4 z = 0 } \\ { 3 x - 5 y + 3 z = - 10 } \\ { 5 x - 2 y + 5 z = - 4 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x - 2 y + 9 z = 2 } \\ { - 2 x - 5 y - 4 z = 3 } \\ { 5 x - 3 y + 3 z = 15 } \end{array} \right.$
$\left\{ \begin{array} { l } { 8 x + 2 y = - 13 } \\ { - 2 y + z = 1 } \\ { 12 x - 5 z = - 18 } \end{array} \right.$
$\left\{ \begin{array} { l } { x - 3 z = 2 } \\ { y + 6 z = 4 } \\ { 2 x + 3 y = 12 } \end{array} \right.$
$\left\{ \begin{aligned} 9 x + 3 y - 11 z & = 6 \\ 2 x + y - 3 z & = 1 \\ 7 x + 2 y - 8 z & = 3 \end{aligned} \right.$
$\left\{ \begin{array} { c } { 3 x - y - z = 4 } \\ { - 5 x + y + 2 z = - 3 } \\ { 6 x - 2 y - 2 z = 8 } \end{array} \right.$
$\left\{ \begin{array} { l } { 2 x - 4 y + 3 z = 15 } \\ { 3 x - 5 y + 2 z = 18 } \\ { 5 x + 2 y - 6 z = 0 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x - 4 y - 3 z = - 14 } \\ { 4 x + 2 y + 5 z = 12 } \\ { - 5 x + 8 y - 4 z = - 3 } \end{array} \right.$

Answer

1. $\left( \frac { 1 } { 3 } , - \frac { 1 } { 3 } \right)$

3. $\left( \frac { 3 } { 2 } , 0 \right)$

5. $( 6 , - 2 )$

7. $\varnothing$

9. $(0,0)$

11. $\left( x , \frac { 2 } { 3 } x - \frac { 4 } { 3 } \right)$

13. $(2, 3, 3)$

15. $(0, 1, 3)$

17. $(1, -1, 2)$

19. $(\left( \frac { 1 } { 2 } , \frac { 1 } { 2 } , - \frac { 1 } { 2 } \right)$

21. $\varnothing$

23. $(-7, -13, 7)$

25. $(1, 0, \frac{1}{2})$

27. $\left( - 8 , - \frac { 1 } { 2 } z + \frac { 5 } { 2 } , z \right)$

29. $(-1, 2, 1)$

31. $\left( - \frac { 3 } { 2 } , - \frac { 1 } { 2 } , 0 \right)$

33. $\varnothing$

35. $(2, -2, 1)$

Exercise $\PageIndex{7}$

Research and discuss the history of Gaussian Elimination. Who is credited for first developing this process? Post something that you found interesting relating to this story.
Research and discuss the history of modern matrix notation. Who is credited for the development? In what fields are they used today? Post your findings on the discussion board.

Answer: 1. Answer may vary

Footnotes

²²A linear system consisting of equations with three variables in standard form arranged so that the variable $x$ does not appear after the first equation and the variable $y$ does not appear after the second equation.

²³A rectangular array of numbers consisting of rows and columns.

²⁴The matrix of coefficients of a linear system in standard form written as they appear lined up without the variables or operations.

²⁵The coefficient matrix with the column of constants included.

²⁶Operations that can be performed to obtain equivalent linear systems.

²⁷Steps used to obtain an equivalent linear system in upper triangular form so that it can be solved using back substitution.

²⁸A matrix in triangular form where the leading nonzero element of each row is 1