9.3E: Double-Angle, Half-Angle, and Reduction Formulas (Exercises)
- Page ID
- 56112
For the following exercises, find the exact value.
20. Find \(\sin (2 \theta), \cos (2 \theta),\) and \(\tan (2 \theta)\) given \(\cos \theta=-\frac{1}{3}\) and \(\theta\) is in the interval \(\left[\frac{\pi}{2}, \pi\right]\).
21. Find \(\sin (2 \theta), \cos (2 \theta),\) and \(\tan (2 \theta)\) given sec \(\theta=-\frac{5}{3}\) and \(\theta\) is in the interval \(\left[\frac{\pi}{2}, \pi\right]\).
22. \(\sin \left(\frac{7 \pi}{8}\right)\)
23. \(\sec \left(\frac{3 \pi}{8}\right)\)
For the following exercises, use Figure 1 to find the desired quantities.
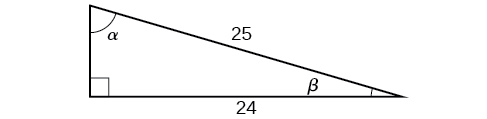
Figure 1
24. \(\sin (2 \beta), \cos (2 \beta), \tan (2 \beta), \sin (2 \alpha), \cos (2 \alpha),\) and \(\tan (2 \alpha)\)
25. \(\sin \left(\frac{\beta}{2}\right), \cos \left(\frac{\beta}{2}\right), \tan \left(\frac{\beta}{2}\right), \sin \left(\frac{\alpha}{2}\right), \cos \left(\frac{\alpha}{2}\right),\) and \(\tan \left(\frac{\alpha}{2}\right)\)
For the following exercises, prove the identity.
26. \(\frac{2 \cos (2 x)}{\sin (2 x)}=\cot x-\tan x\)
27. \(\cot x \cos (2 x)=-\sin (2 x)+\cot x\)
For the following exercises, rewrite the expression with no powers.
28. \(\cos ^{2} x \sin ^{4}(2 x)\)
29. \(\tan ^{2} x \sin ^{3} x\)


