1.4: Fractions

In our previous section we identified integers: \(0,\pm 1,\pm 2,\pm 3, \ldots .\) To this set, now we will add all ratios of integers with non-zero denominators, like \(\frac{2}{7}, \frac{-11}{17} \ldots\) We call this the set of rational numbers. Any rational number looks like \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q\) is not \(0 .\)

Just as we are able to perform arithmetic operations with integers we can also perform arithmetic operations with rational numbers (fractions). The two types of fractions we will encounter are called proper and improper:

• Proper fractions have value less than \(1,\) for example \(\frac{2}{5}\) and \(\frac{1}{8} .\) Observe that for these fractions the numerator is less than the denominator.
• Improper fractions have value greater than or equal to \(1,\) for example \(\frac{7}{6}\) and \(\frac{3}{2} .\) For these fractions the numerator is greater than the denominator.

Each fractional value can have many different, equivalent forms, for example \(1=\frac{2}{2}=\frac{-5}{-5}=\ldots\) In order to determine whether two fractions are equivalent we can use the fundamental principle of fractions.

The Fundamental Principle of Fractions

\[\frac{2}{3}=\frac{2 \cdot 4}{3 \cdot 4}=\frac{8}{12}\nonumber\]

That is, as long as you multiply both numerator and denominator by the same number, the fraction value does not change, and you obtain equivalent fractions.

Example 2.1

Write a fraction that is equivalent to \(\frac{3}{5}\).

Solution

Begin with our original fraction \(\frac{3}{5}\) and apply the fundamental principle of fractions to get

\[\frac{3}{5}=\frac{3 \cdot 2}{5 \cdot 2}=\frac{6}{10}\nonumber\]

Example 2.2

Simplify the fraction \(\frac{15}{35}\).

Solution

Begin with our original fraction and apply the fundamental principle of fractions in reverse to get

\[\frac{15}{35}=\frac{3 \cdot 5}{7 \cdot 5}=\frac{3}{7}\nonumber\]

Multiplying Fractions

We multiply numerators together and denominators together:

\[\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}\nonumber\]

Example 2.3

The product of these two fractions is done as follows:

\[\frac{14 \cdot 9}{3 \cdot 7}=\frac{2 \cdot 7 \cdot 3 \cdot 3}{3 \cdot 7}=\frac{6}{1}=6\nonumber\]

The Reciprocal of a Fraction

The reciprocal of a fraction \(\frac{p}{q}\) is the fraction formed by switching the numerator and denominator, namely \(\frac{q}{p}\)

Example 2.4

1. The reciprocal of \(\frac{3}{5}\) is \(\frac{5}{3}\).
2. The reciprocal of \(\frac{-2}{7}\) is \(\frac{7}{-2}=\frac{-7}{2}=-\frac{7}{2}\).
3. The reciprocal of \(\frac{1}{8}\) is \(\frac{8}{1}=8\).
4. The reciprocal of \(4=\frac{4}{1}\) is \(\frac{1}{4}\).

Dividing Fractions

We multiply the first fraction by the reciprocal of the second:

\[\frac{a}{b} \div \frac{c}{d}=\frac{a}{b} \cdot \frac{d}{c}=\frac{a \cdot d}{b \cdot c}\nonumber\]

Example 2.5

The quotient of these two fractions is found as follows:

\(\frac{8}{3} \div \frac{4}{5}=\frac{8}{3} \cdot \frac{5}{4}=\frac{8 \cdot 5}{3 \cdot 4} =\frac{2 \cdot 4 \cdot 5}{3 \cdot 4}=\frac{10}{3}\)

Adding Fractions (with same denominators)

\[\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}\nonumber\]

Subtracting Fractions (with same denominators)

\[\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}\nonumber\]

Example 2.6

Add \(\frac{3}{5}+\frac{1}{5}\)

Solution

\[\frac{3}{5}+\frac{1}{5}=\frac{3+1}{5}=\frac{4}{5}\nonumber\]

Adding or Subtracting Fractions (with unlike denominators)

Adding (or subtracting) fractions with unlike denominators requires us to first find a common denominator. The LCD or least common denominator is the smallest number that both denominators evenly divide. Once we rewrite each of our fractions so their denominator is the LCD, we may add or subtract fractions according to the above properties.

Finding the LCD

• Step 1: Make a list of (enough) multiples of each denominator.
• Step 2: Identify the lowest common multiple. If you can’t see one, then your lists in Step 1. need to be expanded.

To be able to add or subtract fractions, we need to go one more step: Once you’ve identified the LCD, rewrite both fractions (by multiplying both numerator and denominator by the appropriate same number) to get the LCD as denominator.

Example 2.7

Find the LCD and then add and simplify \(\frac{3}{12}+\frac{5}{8}\).

Solution

Let us first find the LCD by following our procedure.

Step 1. Make a list of (enough) multiples:

\(8: 8,16,24,32, \ldots\)

\(12: 12,24,36,48, \ldots\)

Step 2. LCD: \(24,8 \cdot 3=24,12 \cdot 2=24\)

Step 3. Rewrite each fraction using the LCD:

\[\frac{3}{12}=\frac{3 \cdot 2}{12 \cdot 2}=\frac{6}{24}\nonumber\]

and

\[\frac{5}{8}=\frac{5 \cdot 3}{8 \cdot 3}=\frac{15}{24}\nonumber\]

Now we are ready to add our fractions

\[\frac{6}{24}+\frac{15}{24}=\frac{21}{24}\nonumber\]

simplifying yields

1. \[\frac{21}{24}=\frac{3 \cdot 7}{3 \cdot 8}=\frac{7}{8}\nonumber\]

Example 2.8

Find the LCD and then subtract and simplify \(\frac{1}{9}-\frac{3}{5}\).

Solution

Let us first find the LCD by following our procedure.

Step 1. Make a list of (enough) multiples:

\(9: 9,18,27,36,45,54,63, \ldots\)

\(5: 5,10,15,20,25,30,35,40,45,50,55, \ldots\)

Step 2. LCD: \(45\)

Step 3. Rewrite each fraction using the LCD:

\[\frac{1}{9}=\frac{1 \cdot 5}{9 \cdot 5}=\frac{5}{45}\nonumber\]

and

\[\frac{3}{5}=\frac{3 \cdot 9}{5 \cdot 9}=\frac{27}{45}\nonumber\]

Now we are ready to subtract our fractions, but, first, we rewrite the subtraction as addition of the opposite:

\[\frac{1}{9}-\frac{3}{5}=\frac{1}{9}+\left(-\frac{3}{5}\right)=\frac{5}{45}+\left(-\frac{27}{45}\right)=\frac{5+(-27)}{45}=\frac{-22}{45}\nonumber\]

Writing an Improper Fraction as a Mixed Number

1. Divide the numerator by the denominator.
2. If there is a remainder, write it over the denominator.

Example 2.9

Write \(\frac{42}{5}\) as a mixed number.

Solution

We begin by dividing the numerator \(42\) by the denominator \(5\) to get \(8,\) with a remainder of \(2\). Our mixed number is \(8 \frac{2}{5}\).

Writing a Mixed Number as an Improper Fraction

1. Multiply the whole number and the denominator then add the numerator. Use the result as your new numerator.
2. The denominator remains the same

Example 2.10

Write the mixed number \(3 \frac{5}{6}\) as an improper fraction.

Solution

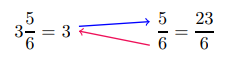1. Multiply the denominator by the whole number.
2. Add this result to the numerator.
3. Set this new numerator 23 over the denominator of 6.

We multiply the whole number 3 and the denominator 6 to get \(18 .\) Next, we add to this the numerator 5 to get \(23 .\) This is our new numerator and our improper fraction becomes \(\frac{23}{6}\).

Addition and Subtraction of Mixed Numbers

To add (or subtract) mixed numbers, we can convert the numbers into improper fractions, then add (or subtract) the fractions as we saw in this chapter.

Example \(\PageIndex{1}\)

Subtract \(7-2 \frac{3}{8}\).

Solution

First we convert \(2 \frac{3}{8}=\frac{19}{8}\). Then, we rewrite the subtraction operation as addition of opposite:

\[7-\frac{19}{8}=7+\left(-\frac{19}{8}\right)=\frac{7}{1}+\left(-\frac{19}{8}\right)=\frac{56}{8}+\left(-\frac{19}{8}\right)=\frac{56+(-19)}{8}=\frac{37}{8}=4 \frac{5}{8}\nonumber\]

Also, we can keep mixed fractions and mixed fraction, and, add (or subtract) the integer parts together and the fraction parts together.

Example 2.12

Add \(7 \frac{3}{4}+3 \frac{1}{5}\)

Solution

Here, we add \(7+3=10\) and \(\frac{3}{4}+\frac{1}{5}=\frac{15}{20}+\frac{4}{20}=\frac{19}{20}\).

And, our final answer is \(10 \frac{19}{20}\). Note that \(\frac{19}{20}\) is a proper fraction, so, our work is done. But, if our answer ended up with an improper fraction, we would have had to make the conversion to write the answer in simplified form.

Multiplying and Dividing of Mixed Numbers

Be careful when multiplying mixed numbers. You must first convert them to improper fractions and use the rules for multiplying fractions to finish your problem.

Example 2.13

Multiply \(2 \frac{3}{5}\) and \(3 \frac{1}{2}\).

Solution

Begin by rewriting each mixed number as an improper fraction: \(2 \frac{3}{5}=\frac{13}{5}\) and \(3 \frac{1}{2}=\frac{7}{2}\). Now we proceed by multiplying the fractions

\[\frac{13}{5} \cdot \frac{7}{2}=\frac{13 \cdot 7}{5 \cdot 2}=\frac{91}{10}\nonumber\]

We can now write the result (if we wish) as a mixed number: \(9 \frac{1}{10}\).

Example 2.14

Divide \(\left(1 \frac{4}{5}\right) \div\left(1 \frac{1}{2}\right)\)

Solution

Begin by rewriting each mixed number as a improper fraction: \(1 \frac{4}{5}=\frac{9}{5}\) and \(1 \frac{1}{2}=\frac{3}{2} .\) Now we proceed by dividing the fractions

\[\frac{9}{5} \div \frac{3}{2}=\frac{9}{5} \cdot \frac{2}{3}=\frac{9 \cdot 2}{5 \cdot 3}=\frac{3 \cdot 2}{5 \cdot 1}=\frac{6}{5}=1 \frac{1}{5}\nonumber\]

Exit Problem

Evaluate: \(\frac{3}{4}-1 \frac{5}{6}\).