1.1: Real numbers and the Number Line
- Page ID
- 18326
SKILLS TO DEVELOP
- Construct a number line and graph points on it.
- Use a number line to determine the order of real numbers.
- Determine the opposite of a real number.
- Determine the absolute value of a real number.
Definitions
A set is a collection of objects, typically grouped within braces \(\{\) \(\}\), where each object is called an element. For example, \(\{\text{red, green, blue}\}\) is a set of colors. A subset is a set consisting of elements that belong to a given set. For example, \(\{\text{green, blue}\}\) is a subset of the color set above. A set with no elements is called the empty set and has its own special notation, \(\{\) \(\}\) or \(\varnothing\).
When studying mathematics, we focus on special sets of numbers. The set of natural (or counting) numbers, denoted \(\mathbb{N}\), is
\( \{1,2,3,4,5 , \dots \} \quad \color{Cerulean}{Natural\: Numbers} \)
The three periods \((\dots)\) is called an ellipsis and indicates that the numbers continue without bound. The set of whole numbers, denoted \(\mathbb{W}\), is the set of natural numbers combined with zero.
\( \{0,1,2,3,4,5 , \dots\} \quad \color{Cerulean}{Whole\: Numbers} \)
The set of integers, denoted \(\mathbb{Z}\), consists of both positive and negative whole numbers, as well as zero.
\( \{\dots, -3,-2,-1,0,1,2,3 , \dots\} \quad \color{Cerulean}{Integers} \)
Notice that the sets of natural and whole numbers are both subsets of the set of integers.
Rational numbers, denoted \(\mathbb{Q}\), are defined as any number of the form \(\dfrac{a}{b}\), where \(a\) and \(b\) are integers and \(b\) is nonzero. Decimals that repeat or terminate are rational. For example,
\(0.7= \frac{7}{10} \quad \text{and} \quad 0. \overline{3} =0.3333 \dots = \frac{1}{3}\)
The set of integers is a subset of the set of rational numbers because every integer can be expressed as a ratio of the integer and \(1\). In other words, any integer can be written over \(1\) and can be considered a rational number. For example,
\(5= \frac{5}{1}\)
Irrational numbers are defined as any number that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example,
\(\pi =3.14159 \dots \quad \text{and} \quad \sqrt{2} = 1.41421 \dots\)
The set of real numbers, denoted \(\mathbb{R}\), is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,

Number Line
A real number line, or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinate. A point on the real number line that is associated with a coordinate is called its graph.
To construct a number line, draw a horizontal line with arrows on both ends to indicate that it continues without bound. Next, choose any point to represent the number zero; this point is called the origin.
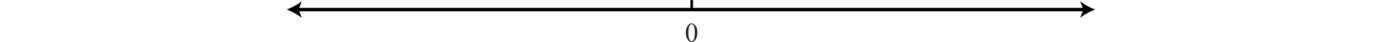
Mark off consistent lengths on both sides of the origin and label each tick mark to define the scale. Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero \((0)\) is neither positive nor negative. Typically, each tick represents one unit.
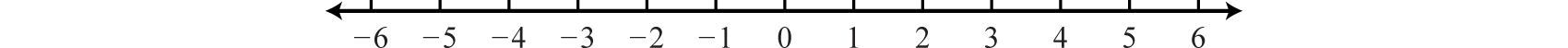
As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents \(\frac{1}{7}\) of a unit.
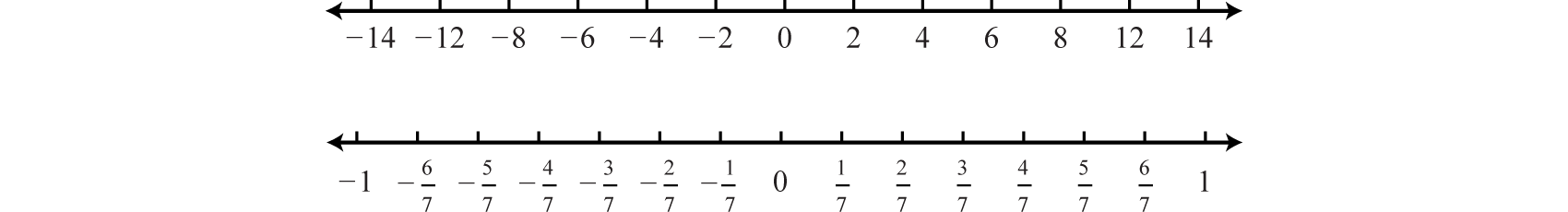
The graph of each real number is shown as a dot at the appropriate point on the number line. A partial graph of the set of integers \(\mathbb{Z}\) follows:

Example \(\PageIndex{1}\)
Graph the following set of real numbers:
Solution
Graph the numbers on a number line with a scale where each tick mark represents \(\frac{1}{2}\) of a unit.
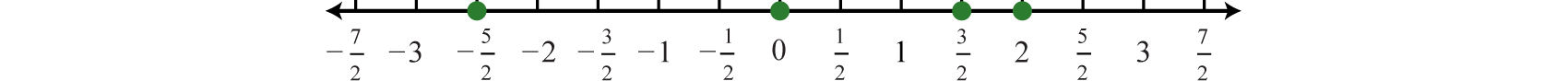
Ordering Real Numbers
When comparing real numbers on a number line, the larger number will always lie to the right of the smaller one. It is clear that \(15\) is greater than \(5\), but it may not be so clear to see that \(−1\) is greater than \(−5\) until we graph each number on a number line.
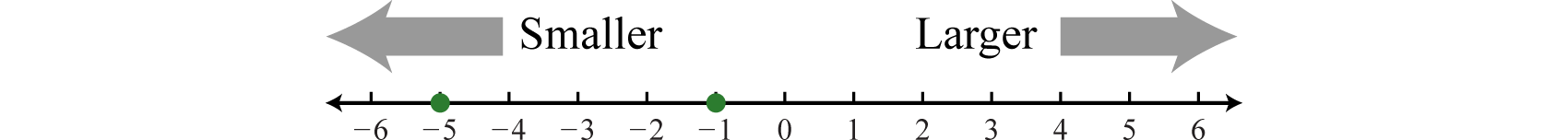
We use symbols to help us efficiently communicate relationships between numbers on the number line. The symbols used to describe an equality relationship between numbers follow:
\[\begin{align*} &= \quad \color{Cerulean}{is\ equal\ to} \\ &\neq \quad \color{Cerulean}{is\ not\ equal\ to} \\ &\approx \quad \color{Cerulean}{is\ approximately\ equal\ to} \end{align*}\]
These symbols are used and interpreted in the following manner:
\[\begin{align*} &5=5 \qquad &&\color{Cerulean}{5\ is\ equal\ to\ 5} \\ &0 \neq 5 \qquad &&\color{Cerulean}{0\ is\ not\ equal\ to\ 5} \\ &\pi \approx 3.14 \quad &&\color{Cerulean}{pi\ is\ approximately\ equal\ to\ 3.14} \end{align*}\]
We next define symbols that denote an order relationship between real numbers.
\[\begin{align*} &< \quad \color{Cerulean}{Less\ than} \\ &> \quad \color{Cerulean}{Greater\ than} \\ &\leq \quad \color{Cerulean}{Less\ than\ or\ equal\ to} \\ &\geq \quad \color{Cerulean}{Greater\ than\ or\ equal\ to} \end{align*}\]
These symbols allow us to compare two numbers. For example,
Since the graph of \(−120\) is to the left of the graph of \(–10\) on the number line, that number is less than \(−10\). We could write an equivalent statement as follows:
Similarly, since the graph of zero is to the right of the graph of any negative number on the number line, zero is greater than any negative number.
The symbols \(<\) and \(>\) are used to denote strict inequalities, and the symbols and are used to denote inclusive inequalities. In some situations, more than one symbol can be correctly applied. For example, the following two statements are both true:
In addition, the “or equal to” component of an inclusive inequality allows us to correctly write the following:
The logical use of the word “or” requires that only one of the conditions need be true: the “less than” or the “equal to.”
Example \(\PageIndex{2}\)
Fill in the blank with \(<, =\), or \(>: −2\) ____ \(−12\).
Solution
Use > because the graph of \(−2\) is to the right of the graph of \(−12\) on a number line. Therefore, \(−2 > −12\), which reads “negative two is greater than negative twelve.”

Answer:
\(-2>-12\)
In this text, we will often point out the equivalent notation used to express mathematical quantities electronically using the standard symbols available on a keyboard. We begin with the equivalent textual notation for inequalities:
\[\begin{align*} &\geq &&">=" \\ &\leq &&"<=" \\ &\neq &&"!=" \end{align*}\]
Many calculators, computer algebra systems, and programming languages use this notation.
Opposites
The opposite of any real number \(a\) is \(−a\). Opposite real numbers are the same distance from the origin on a number line, but their graphs lie on opposite sides of the origin and the numbers have opposite signs.
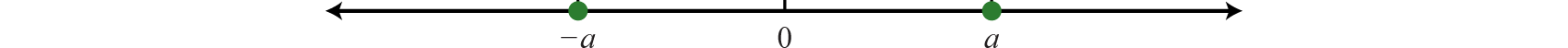
For example, we say that the opposite of \(10\) is \(−10\).
Next, consider the opposite of a negative number. Given the integer \(−7\), the integer the same distance from the origin and with the opposite sign is \(+7\), or just \(7\).

Therefore, we say that the opposite of \(−7\) is \(−(−7) = 7\). This idea leads to what is often referred to as the double-negative property. For any real number \(a\),
\(-(-a)=a\)
Example \(\PageIndex{3}\)
What is the opposite of \(-\frac{3}{4}\)?
Solution
Here we apply the double-negative property.
\(-(-\frac{3}{4})=\frac{3}{4}\)
Example \(\PageIndex{4}\)
Simplify \(-(-(4))\)
Solution
Start with the innermost parentheses by finding the opposite of \(+4\).
\[\begin{align*} -(-(4)) &= -(\color{Cerulean}{-(4)} \color{Black}{)} \\ &= -(\color{Cerulean}{-4} \color{Black}{)} \\ &=4 \end{align*}\]
Answer
4
Example \(\PageIndex{5}\)
Simplify: \(-(-(-2))\).
Solution
Apply the double-negative property starting with the innermost parentheses.
\[\begin{align*} -(-(-2)) &= -(\color{Cerulean}{-(-2)} \color{Black}{)} \\ &= -(\color{Cerulean}{2} \color{Black}{)} \\ &=-2 \end{align*}\]
Answer
-2
tip
If there is an even number of consecutive negative signs, then the result is positive. If there is an odd number of consecutive negative signs, then the result is negative.
Try this!
Exercise \(\PageIndex{1}\)
Simplify: \(-(-(-(5)))\).
- Answer
-
-5
Procedure:
\[\begin{align*} -(-(-(5))) &= -(\color{Cerulean}{-(-(5))} \color{Black}{)}\\ &= -(\color{Cerulean}{-(-5)} \color{Black}{)} \\ &= -(\color{Cerulean}{5} \color{Black}{)} \\&= -5 \end{align*} \]
Video Solution:
(click to see video)
Absolute Value
The absolute value of a real number \(a\), denoted \(|a|\), is defined as the distance between zero (the origin) and the graph of that real number on the number line. Since it is a distance, it is always positive. For example,
\(|-4|=4 \quad \text{and} \quad |4|=4\)
Both \(4\) and \(−4\) are four units from the origin, as illustrated below:
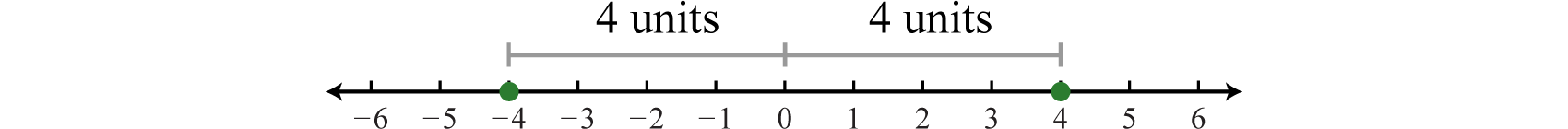
Example \(\PageIndex{6}\)
Simplify:
a. \(|-12|\)
b.\(|12|\)
Solution
Both \(−12\) and \(12\) are twelve units from the origin on a number line. Therefore,
\(|-12|=12 \quad \text{and} \quad |12|=12\)
Answer
a.\(12\) b.\(12\)
Also, it is worth noting that
\(|0|=0\)
The absolute value can be expressed textually using the notation abs\((a)\). We often encounter negative absolute values, such as \(−|3|\) or \(−\) abs\((3)\). Notice that the negative sign is in front of the absolute value symbol. In this case, work the absolute value first and then find the opposite of the result.
Try not to confuse this with the double-negative property, which states that \(−(−7)=+7\).
Example \(\PageIndex{7}\)
Simplfy: \(-|-(-7)|\).
Solution
First, find the opposite of \(−7\) inside the absolute value. Then find the opposite of the result.
\[\begin{align*} -|\color{Cerulean}{-(-7)} \color{Black}{|} &= -|\color{Cerulean}{7} \color{Black}{|} \\ &=-7 \end{align*}\]
Answer
-7
At this point, we can determine what real numbers have a particular absolute value. For example,
\(|?|=5\)
Think of a real number whose distance to the origin is \(5\) units. There are two solutions: the distance to the right of the origin and the distance to the left of the origin, namely, \(\{\pm 5\}\). The symbol \( (\pm) \) is read “plus or minus” and indicates that there are two answers, one positive and one negative.
\(|-5|=5\ \quad \text{and} \quad |5|=5\)
Now consider the following:
\(|?|=-5\)
Here we wish to find a value for which the distance to the origin is negative. Since negative distance is not defined, this equation has no solution. If an equation has no solution, we say the solution is the empty set: \(\varnothing\).
Key Takeaways
- Any real number can be associated with a point on a line.
- Create a number line by first identifying the origin and marking off a scale appropriate for the given problem.
- Negative numbers lie to the left of the origin and positive numbers lie to the right.
- Smaller numbers always lie to the left of larger numbers on the number line.
- The opposite of a positive number is negative and the opposite of a negative number is positive.
- The absolute value of any real number is always positive because it is defined to be the distance from zero (the origin) on a number line.
- The absolute value of zero is zero.
Exercise \(\PageIndex{2}\)
Use set notation to list the described elements.
- The hours on a clock.
- The days of the week.
- The first ten whole numbers.
- The first ten natural numbers.
- The first five positive even integers.
- The first five positive odd integers.
- Answer
-
1. \(\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}\)
3. \(\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\)
5. \(\{2, 4, 6, 8, 10\}\)
Exercise \(\PageIndex{3}\)
Determine whether the following real numbers are integers, rational, or irrational.
- \(12\)
- \(−3\)
- \(4.5\)
- \(−5\)
- \(0.3 \overline{6} \)
- \(0. \overline{3} \)
- \(1.001000100001 \dots\)
- \(1.00 \overline{1} \)
- \(e=2.71828 \dots \)
- \(\sqrt{7}=2.645751 \dots \)
- \(−7\)
- \(3.14\)
- \(227\)
- \(1.33\)
- \(0\)
- \(8,675,309\)
- Answer
-
1: Integer, Rational
3: Rational
5: Rational
7: Irrational
9: Irrational
11: Integer, Rational
13: Rational
15: Integer, Rational
Exercise \(\PageIndex{4}\)
True or false.
- All integers are rational numbers.
- All integers are whole numbers.
- All rational numbers are whole numbers.
- Some irrational numbers are rational.
- All terminating decimal numbers are rational.
- All irrational numbers are real.
- Answer
-
1: True
3: False
5: True
Exercise \(\PageIndex{5}\)
Choose an appropriate scale and graph the following sets of real numbers on a number line.
- \(\{−3, 0, 3\}\)
- \(\{−2, 2, 4, 6, 8, 10\}\)
- \(\{−2, −1/3, 2/3, 5/3\}\)
- \(\{−5/2, −1/2, 0, 1/2 , 2\}\)
- \(\{−5/7, 0, 2/7 , 1\}\)
- \(\{ –5, –2, –1, 0\}\)
- \(\{ −3, −2, 0, 2, 5\}\)
- \(\{−2.5, −1.5, 0, 1, 2.5\}\)
- \(\{0, 0.3, 0.6, 0.9, 1.2\}\)
- \(\{−10, 30, 50\}\)
- \(\{−6, 0, 3, 9, 12\}\)
- \(\{−15, −9, 0, 9, 15\}\)
- Answer
-
1. \(\{−3, 0, 3\}\)

Figure \(\PageIndex{12}\) 3. \(\{−2, −1/3, 2/3, 5/3\}\)

Figure \(\PageIndex{13}\) 5. \(\{−5/7, 0, 2/7 , 1\}\)

Figure \(\PageIndex{14}\) 7. \(\{ −3, −2, 0, 2, 5\}\)

Figure \(\PageIndex{15}\) 9. \(\{0, 0.3, 0.6, 0.9, 1.2\}\)

Figure \(\PageIndex{16}\) 11. \(\{−6, 0, 3, 9, 12\}\)

Figure \(\PageIndex{17}\)
Exercise \(\PageIndex{6}\)
Fill in the blank with \(<, =\), or \(>\).
- \(−7\) ___ \(0\)
- \(30\) ___ \(2\)
- \(10\) ___ \(−10\)
- \(−150\) ___ \(−75\)
- \(−0.5\) ___ \(−1.5\)
- \(0\) ___ \(0\)
- \(-500\) ___ \(200\)
- \(−1\) ___ \(−200\)
- \(−10\) ___ \(−10\)
- \(−40\) ___ \(−41\)
- Answer
-
1. \(<\)
3. \(>\)
5. \(>\)
7. \(<\)
9. \(=\)
Exercise \(\PageIndex{7}\)
True or false.
- \(5≠7\)
- \(4=5\)
- \(1≠1\)
- \(−5>−10\)
- \(4 \leq 4\)
- \(−12 \geq 0\)
- \(−10=−10\)
- \(3>3\)
- \(−1000<−20\)
- \(0=0\)
- Answer
-
1. True
3. False
5. True
7. True
9. True
Exercise \(\PageIndex{8}\)
List the numbers.
- List three integers less than \(−5\).
- List three integers greater than \(−10\).
- List three rational numbers less than zero.
- List three rational numbers greater than zero.
- List three integers between \(−20\) and \(−5\).
- List three rational numbers between \(0\) and \(1\).
- Answer
-
1. \(−10, −7, −6\) (answers may vary)
3. \(−1, −2/3, −1/3\) (answers may vary)
5. \(−15, −10, −7\) (answers may vary)
Exercise \(\PageIndex{9}\)
Translate each statement into an English sentence.
- \(10<20\)
- \(−50 \leq −10\)
- \(−4 \neq 0\)
- \(30 \geq −1\)
- \(0=0\)
- \(e \approx 2.718\)
- Answer
-
1. Ten is less than twenty.
3. Negative four is not equal to zero.
5. Zero is equal to zero.
Exercise \(\PageIndex{10}\)
Translate the following into a mathematical statement.
- Negative seven is less than zero.
- Twenty-four is not equal to ten.
- Zero is greater than or equal to negative one.
- Four is greater than or equal to negative twenty-one.
- Negative two is equal to negative two.
- Negative two thousand is less than negative one thousand.
- Answer
-
1. \(−7<0\)
3. \(0 \geq −1\)
5. \(−2=−2\)
Exercise \(\PageIndex{11}\)
Simplify.
- \(−(−9)\)
- \(−(−35)\)
- \(−(10)\)
- \(−(3)\)
- \(−(5)\)
- \(−(34)\)
- \(−(−1)\)
- \(−(−(−1))\)
- \(−(−(1))\)
- \(−(−(−3))\)
- \(−(−(−(−11)))\)
- Answer
-
1. \(9\)
3. \(−10\)
5. \(−5\)
7. \(1\)
9. \(1\)
11. \(11\)
Exercise \(\PageIndex{12}\)
Answer the following questions.
- What is the opposite of \(-12\)
- What is the opposite of \(\pi \) ?
- What is the opposite \(−0.01\)?
- Is the opposite of \(−12\) smaller or larger than \(−11\)?
- Is the opposite of \(7\) smaller or larger than \(−6\)?
- Answer
-
2. \(-\pi \)
4. Larger
Exercise \(\PageIndex{13}\)
Fill in the blank with \(<, =\), or \(>\).
- \(−7\) ___ \(−(−8)\)
- \(6\) ___ \(−(6)\)
- \(13\) ___ \(−(−12)\)
- \(−(−5)\) ___ \(−(−2)\)
- \(−100\) ___ \(−(−(−50))\)
- \(44\) ___ \(−(−44)\)
- Answer
-
1. \(<\)
3. \(>\)
5. \(<\)
Exercise \(\PageIndex{14}\)
Simplify.
- \(|20|\)
- \(|−20|\)
- \(|−33|\)
- \(|−0.75|\)
- \(|−\frac{3}{5}|\)
- \(|38|\)
- \(|0|\)
- \(|1|\)
- \(−|12|\)
- \(−|−20|\)
- \(−|20|\)
- \(−|−8|\)
- \(−|7|\)
- \(−|−316|\)
- \(−(−|\frac{8}{9}|)\)
- \(|−(−2)|\)
- \(−|−(−3)|\)
- \(−(−|5|)\)
- \(−(−|−45|)\)
- \(−|−(−21)|\)
- abs\((6)\)
- abs\((−7)\)
- \(−\)abs\((5)\)
- \(−\)abs\((−19)\)
- \(−(−\)abs\((9))\)
- \(−\)abs\((−(−12))\)
- Answer
-
1. \(20\)
3. \(33\)
5. \(\frac{3}{5}\)
7. \(0\)
9. \(−12\)
11. \(−20\)
13. \(−7\)
15. \(\frac{8}{9}\)
17. \(−3\)
19. \(45\)
21. \(6\)
23. \(−5\)
25. \(9\)
Exercise \(\PageIndex{15}\)
Determine the unknown.
- \(| ? |=9\)
- \(| ? |=15\)
- \(| ? |=0\)
- \(| ? |=1\)
- \(| ? |=−8\)
- \(| ? |=−20\)
- \(|?|−10=−2\)
- \(|?|+5=14\)
- Answer
-
1. \(\pm 9\)
3. \(0\)
5. \(\varnothing\), No solution
7. \(\pm 8\)
Exercise \(\PageIndex{16}\)
Fill in the blank with \(<, =\), or \(>\).
- \(|−2|\) ____ \(0\)
- \(|−7|\) ____ \(|−10|\)
- \(−10\) ____ \(−|−2|\)
- \(|−6|\) ____ \(|−(−6)|\)
- \(−|3|\) ____ \(|−(−5)|\)
- \(0\) ____ \(−|−(−4)|\)
- Answer
-
1. \(>\)
3. \(<\)
5. \(<\)
Exercise \(\PageIndex{17}\)
Discussion Board Topics.
- Research and discuss the history of the number zero.
- Research and discuss the various numbering systems throughout history.
- Research and discuss the definition and history of \(\pi\).
- Research the history of irrational numbers. Who is credited with proving that the square root of \(2\) is irrational and what happened to him?
- Research and discuss the history of absolute value.
- Discuss the “just make it positive” definition of absolute value


