5.1: Rules of Exponents
- Page ID
- 18354
Learning Objectives
- Simplify expressions using the rules of exponents.
- Simplify expressions involving parentheses and exponents.
- Simplify expressions involving \(0\) as an exponent.
Product, Quotient, and Power Rule for Exponents
If a factor is repeated multiple times, then the product can be written in exponential form \(x_{n}\). The positive integer exponent \(n\) indicates the number of times the base \(x\) is repeated as a factor
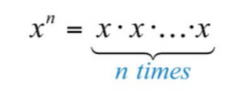.png?revision=1)
For example,
\(5^{4}=5\cdot 5\cdot 5\cdot 5\)
Here the base is \(5\) and the exponent is \(4\). Exponents are sometimes indicated with the caret (^) symbol found on the keyboard: \(5\)^\(4 = 5*5*5*5\).
Next consider the product of \(2^{3}\) and \(2^{5}\),
.png?revision=1&size=bestfit&width=331&height=81)
Expanding the expression using the definition produces multiple factors of the base, which is quite cumbersome, particularly when \(n\) is large. For this reason, we will develop some useful rules to help us simplify expressions with exponents. In this example, notice that we could obtain the same result by adding the exponents.
\(2^{3}\cdot 2^{5}=2^{3+5}=2^{8}\)
In general, this describes the product rule for exponents. If \(m\) and \(n\) are positive integers, then
\[x^{m}\cdot x^{n} = x^{m+n}\]
In other words, when multiplying two expressions with the same base, add the exponents.
Example \(\PageIndex{1}\)
Simplify: \(10^{5}\cdot 10^{18}\).
Solution:
\(\begin{aligned} 10^{5}\cdot 10^{18}&=10^{5+18} \\ &=10^{23} \end{aligned}\)
Answer:
\(10^{23}\)
In the previous example, notice that we did not multiply the base 10 times itself. When applying the product rule, add the exponents and leave the base unchanged.
Example \(\PageIndex{2}\)
Simplify: \(x^{6}⋅x^{12}⋅x\).
Solution:
Recall that the variable \(x\) is assumed to have an exponent of \(1: x=x^{1}\).
\(\begin{aligned} x^{6}\cdot x^{12}\cdot x &=x^{6}\cdot x^{12}\cdot x^{1} \\ &=x^{6+12+1} \\ &=x^{19} \end{aligned}\)
Answer:
\(x^{19}\)
The base could be any algebraic expression.
Example \(\PageIndex{3}\)
Simplify: \((x+y)^{9} (x+y)^{13}\).
Solution:
Treat the expression \((x+y)\) as the base.
\(\begin{aligned} (x+y)^{9}(x+y)^{13}&=(x+y)^{9+13} \\ &=(x+y)^{22} \end{aligned}\)
Answer:
\((x+y)^{22}\)
The commutative property of multiplication allows us to use the product rule for exponents to simplify factors of an algebraic expression.
Example \(\PageIndex{4}\)
Simplify: \(2x^{8}y⋅3x^{4}y^{7}\).
Solution:
Multiply the coefficients and add the exponents of variable factors with the same base.
\(\begin{aligned} 2x^{8}y\cdot 3x^{4}y^{7}&=2\cdot 3\cdot x^{8}\cdot x^{4}\cdot y^{1}\cdot y^{7} &\color{Cerulean}{Commutative\:property} \\ &=6\cdot x^{8+4}\cdot y^{1+7} &\color{Cerulean}{Power\:rule\:for\:exponents} \\ &=6x^{12}y^{8} \end{aligned}\)
Answer:
\(6x^{12}y^{8}\)
Next, we will develop a rule for division by first looking at the quotient of \(2^{7}\) and \(2^{3}\).
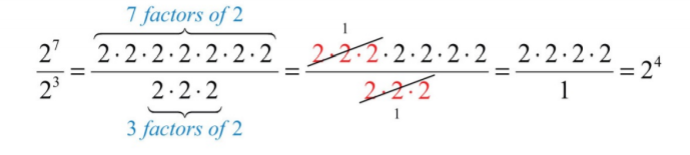.png?revision=1&size=bestfit&width=603&height=135)
Here we can cancel factors after applying the definition of exponents. Notice that the same result can be obtained by subtracting the exponents.
\[\frac{2^{7}}{2^{3}}=2^{7-3}=2^{4} \nonumber\]
This describes the quotient rule for exponents. If \(m\) and \(n\) are positive integers and \(x≠0\), then
\[\frac{x^{m}}{x^{n}}=x^{m-n} \nonumber\]
In other words, when you divide two expressions with the same base, subtract the exponents.
Example \(\PageIndex{5}\)
Simplify: \(\frac{12y^{15}}{4y^{7}}\).
Solution:
Divide the coefficients and subtract the exponents of the variable \(y\).
\(\begin{aligned} \frac{12y^{15}}{4y^{7}}&=\frac{12}{4}\cdot y^{15-7}\\ &=3y^{8} \end{aligned}\)
Answer:
\(3y^{8}\)
Example \(\PageIndex{6}\)
Simplify: \(\frac{20x^{10}(x+5)^{6}}{10x^{9}(x+5)^{2}}\)
Solution:
\(\begin{aligned} \frac{20x^{10}(x+5)^{6}}{10x^{9}(x+5)^{2}}&=\frac{20}{10}\cdot x^{10-9}\cdot (x+5)^{6-2} \\ &=2x^{1}(x+5)^{4} \end{aligned}\)
Answer:
\(2x(x+5)^{4}\)
Now raise \(2^{3}\) to the fourth power as follows:
.png?revision=1&size=bestfit&width=351&height=170)
After writing the base \(2^{3}\) as a factor four times, expand to obtain \(12\) factors of \(2\). We can obtain the same result by multiplying the exponents.
\((2^{3})^{^{4}} = 2^{3\cdot 4} = 2^{12}\)
In general, this describes the power rule for exponents. Given positive integers \(m\) and \(n\), then
\[(x^{m})^{^{n}}=x^{m\cdot n}\]
In other words, when raising a power to a power, multiply the exponents.
Example \(\PageIndex{7}\)
Simplify: \((y^{6})^{^{7}}=y^{6\cdot 7}\)
Solution:
\(\begin{aligned} (y^{6})^{^{7}}&=y^{6\cdot 7} \\ &=y^{42} \end{aligned}\)
Answer:
\(y^{42}\)
To summarize, we have developed three very useful rules of exponents that are used extensively in algebra. If given positive integers \(m\) and \(n\), then
- Product rule: \[x^{m}\cdot x^{n}=x^{m+n}\]
- Quotient rule: \[\frac{x^{m}}{x^{n}}=x^{m-n}, x\neq 0\]
- Power rule: \[(x^{m})^{^{n}} = x^{m\cdot n}\]
Exercise \(\PageIndex{1}\)
Simplify: \(y^{5}⋅(y^{4})^{^{6}}\).
- Answer
-
\(y^{29}\)
Power Rules for Products and Quotients
Now we consider raising grouped products to a power. For example,
\(\begin{aligned} (xy)^{4} &= xy\cdot xy\cdot xy\cdot xy \\ &=x\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot y\quad\color{Cerulean}{Commutative\:property} \\ &=x^{4}\cdot y^{4} \end{aligned}\)
After expanding, we have four factors of the product \(xy\). This is equivalent to raising each of the original factors to the fourth power. In general, this describes the power rule for a product. If \(n\) is a positive integer, then
\[(xy)^{n}=x^{n}y^{n}\]
Example \(\PageIndex{8}\)
Simplify: \((2ab)^{7}=2^{7}a^{7}b^{7}\).
Solution:
We must apply the exponent \(7\) to all the factors, including the coefficient, \(2\).
\(\begin{aligned} (2ab)^{7}&=2^{7}a^{7}b^{7} \\ &=128a^{7}b^{7} \end{aligned}\)
If a coefficient is raised to a relatively small power, then present the real number equivalent, as we did in this example: \(2^{7}=128\).
Answer:
\(128a^{7}b^{7}\)
In many cases, the process of simplifying expressions involving exponents requires the use of several rules of exponents.
Example \(\PageIndex{9}\)
Simplify: \((3xy^{3})^{^{4}}\).
Solution:
\(\begin{aligned} (3xy^{3})^{^{4}}&=3^{4}\cdot x^{4}\cdot (y^{3})^{^{4}} &\color{Cerulean}{Power\:rule\:for\:products} \\ &=3^{4}x^{4}y^{3\cdot 4} &\color{Cerulean}{Power\:rule\:for\:exponents} \\ &=81x^{4}y^{12} \end{aligned}\)
Answer:
\(81x^{4}y^{12}\)
Example \(\PageIndex{10}\)
Simplify: \((4x^{2}y^{5}z)^{^{3}}\).
Solution:
\(\begin{aligned} (4x^{2}y^{5}z)^{^{3}}&=4^{3}\cdot(x^{2})^{^{3}}\cdot (y^{5})^{^{3}}\cdot z^{3} \\ &=64x^{6}y^{15}z^{3} \end{aligned}\)
Answer:
\(64x^{6}y^{15}z^{3}\)
Example \(\PageIndex{11}\)
Simplify: \([5(x+y)^{3}]^{^{3}}\)
Solution:
\(\begin{aligned} [5(x+y)^{3}]^{^{3}} &=5^{3}\cdot (x+y)^{9} \\ &=125(x+y)^{9} \end{aligned}\)
Answer:
\(125(x+y)^{9}\)
Next, consider a quotient raised to a power.
\(\begin{aligned} \left( \frac{x}{y} \right) ^{4} &= \frac{x}{y}\cdot \frac{x}{y}\cdot \frac{x}{y}\cdot \frac{x}{y} \\ &=\frac{x\cdot x\cdot x\cdot x}{y\cdot y\cdot y\cdot y} \\ &=\frac{x^{4}}{y^{4}} \end{aligned}\)
Here we obtain four factors of the quotient, which is equivalent to the numerator and the denominator both raised to the fourth power. In general, this describes the power rule for a quotient. If \(n\) is a positive integer and \(y≠0\), then
\[\left( \frac{x}{y} \right) ^{n} = \frac{x^{n}}{y^{n}}\]
In other words, given a fraction raised to a power, we can apply that exponent to the numerator and the denominator. This rule requires that the denominator is nonzero. We will make this assumption for the remainder of the section.
Example \(\PageIndex{12}\)
Simplify: \(\left(\frac{3a}{b} \right) ^{3}\)
Solution:
First, apply the power rule for a quotient and then the power rule for a product.
\(\begin{aligned} \left(\frac{3a}{b} \right) ^{3}&=\frac{(3a)^{3}}{b^{3}} &\color{Cerulean}{Power\:rule\:for\:a\:quotient} \\ &=\frac{3^{3}\cdot a^{3}}{b^{3}} &\color{Cerulean}{Power\:rule\:for\:a\:product} \\ &=\frac{27a^{3}}{b^{3}} \end{aligned}\)
Answer:
\(\frac{27a^{3}}{b^{3}}\)
In practice, we often combine these two steps by applying the exponent to all factors in the numerator and the denominator.
Example \(\PageIndex{13}\)
Simplify: \(\left( \frac{ab^{2}}{2c^{3}} \right)^{5}\)
Solution:
Apply the exponent \(5\) to all of the factors in the numerator and the denominator.
\(\begin{aligned} \left( \frac{ab^{2}}{2c^{3}} \right)^{5}&=\frac{a^{5}(b^{2})^{^{5}}}{2^{5}(c^{3})^{^{5}}} \\ &=\frac{a^{5}b^{10}}{32c^{15}} \end{aligned}\)
Answer:
\(\frac{a^{5}b^{10}}{32c^{15}}\)
Example \(\PageIndex{14}\)
Simplify: \(\left( \frac{5x^{5}(2x-1)^{4}}{3y^{7}} \right) ^{2}\)
Solution:
\(\begin{aligned} \left( \frac{5x^{5}(2x-1)^{4}}{3y^{7}} \right) ^{2} &=\frac{(5x^{5}(2x-1)^{4})^{2}}{(3y^{7})^{^{2}}} &\color{Cerulean}{Power\:rule\:for\:a\:quotient} \\ &=\frac{5^{2}\cdot (x^{5})^{^{2}}\cdot [(2x-1)^{4}]^{2}}{3^{2}\cdot (y^{7})^{^{2}}} &\color{Cerulean}{Power\:rule\:for\:products} \\ &=\frac{25x^{10}(2x-1)^{8}}{9y^{14}} &\color{Cerulean}{Power\:rule\:for\:exponents} \end{aligned}\)
Answer:
\(\frac{25x^{10}(2x-1)^{8}}{9y^{14}}\)
It is a good practice to simplify within parentheses before using the power rules; this is consistent with the order of operations.
Example \(\PageIndex{15}\)
Simplify: \(\left( \frac{-2x^{3}y^{4}z}{xy^{2}} \right)^{4}\)
Solution:
\(\begin{aligned} \left( \frac{-2x^{3}y^{4}z}{xy^{2}} \right)^{4}&=(-2\cdot x^{3-1}\cdot y^{4-2}\cdot z)^{4} &\color{Cerulean}{Simplify\:within\:the\:parentheses\:first.} \\ &=(-2\cdot x^{2}\cdot y^{2} \cdot z)^{4} &\color{Cerulean}{Apply\:the\:power\:rule\:for\:a\:product.} \\ &=(-2)^{4}\cdot (x^{2})^{^{4}}\cdot (y^{2})^{^{4}}\cdot z^{4}&\color{Cerulean}{Apply\:the\:power\:rule\:for\:exponents.} \\ &=16x^{8}y^{8}z^{4} \end{aligned}\)
Answer:
\(16x^{8}y^{8}z^{4}\)
To summarize, we have developed two new rules that are useful when grouping symbols are used in conjunction with exponents. If given a positive integer \(n\), where \(y\) is a nonzero number, then
- Power rule for a product: \[(xy)^{n} = x^{n}y^{n}\]
- Power rule for a quotient: \[\left( \frac{x}{y} \right)^{n} = \frac{x^{n}}{y^{n}}\]
Exercise \(\PageIndex{2}\)
Simplify: \(\left(\frac{4x^{2}(x-y)^{3}}{3yz^{5}} \right)^{3}\)
- Answer
-
\(\frac{64x^{6}(x-y)^{9}}{27y^{3}z^{15}}\)
Zero as an Exponent
Using the quotient rule for exponents, we can define what it means to have \(0\) as an exponent. Consider the following calculation:
\(\color{Cerulean}{1}\color{black}{=\frac{8}{8}=\frac{2^{3}}{2^{3}}=2^{3-3}=}\color{Cerulean}{2^{0}}
Eight divided by \(8\) is clearly equal to \(1\), and when the quotient rule for exponents is applied, we see that a \(0\) exponent results. This leads us to the definition of zero as an exponent, where \(x≠0\):
\[x^{0}=1\]
It is important to note that \(0^{0}\) is undefined. If the base is negative, then the result is still \(+1\). In other words, any nonzero base raised to the \(0\) power is defined to be \(1\). In the following examples, assume all variables are nonzero.
Example \(\PageIndex{16}\)
Simplify:
- \((-5)^{0}\)
- \(-5^{0}\)
Solution:
- Any nonzero quantity raised to the \(0\) power is equal to \(1\).
\((-5)^{0}=1\)
b.In the example \(−5^{0}\), the base is \(5\), not \(−5\).
Answer:
- \(1\)
- \(-1\)
Example \(\PageIndex{17}\)
Simplify:
\((5x^{3}y^{0}z^{2})^{^{2}}\).
Solution:
It is good practice to simplify within the parentheses first.
\(\begin{aligned} (5x^{3}\color{Cerulean}{y^{0}}\color{black}{z^{2})^{^{2}}}&=(5x^{3}\cdot\color{Cerulean}{1}\color{black}{\cdot z^{2})^{2}} \\ &=(5x^{3}z^{2})^{2} \\ &=5^{2}x^{3\cdot 2}z^{2\cdot 2} \\ &=25x^{6}z^{4} \end{aligned}\)
Answer:
\(25x^{6}z^{4}\)
Example \(\PageIndex{18}\)
Simplify:
\(\left( -\frac{8a^{10}b^{5}}{5c^{12}d^{14}} \right) ^{0}\).
Solution:
\(\left( -\frac{8a^{10}b^{5}}{5c^{12}d^{14}} \right) ^{0} =1\)
Answer:
\(1\)
Exercise \(\PageIndex{3}\)
Simplify:
\(5x^{0}\) and \((5x)^{0}\)
- Answer
-
\(5x^{0}=5\) and \((5x)^{0}=1\)
Key Takeaways
- The rules of exponents allow you to simplify expressions involving exponents.
- When multiplying two quantities with the same base, add exponents: \(x^{m}⋅x^{n}=x^{m+n}\).
- When dividing two quantities with the same base, subtract exponents: \(\frac{x^{m}}{x^{n}}=x^{m−n}\).
- When raising powers to powers, multiply exponents: \((x^{m})^{^{n}}=x^{m⋅n}\).
- When a grouped quantity involving multiplication and division is raised to a power, apply that power to all of the factors in the numerator and the denominator: \((xy)^{n}=x^{n}y^{n}\) and \((\frac{x}{y})^{n}=\frac{x^{n}}{y^{n}}\).
- Any nonzero quantity raised to the \(0\) power is defined to be equal to \(1: x^{0}=1\).
Exercise \(\PageIndex{4}\) Product, Quotient, and Power Rule for Exponents
Write each expression using exponential form.
- \((2x)(2x)(2x)(2x)(2x)\)
- \((−3y)(−3y)(−3y)\)
- \(−10⋅a⋅a⋅a⋅a⋅a⋅a⋅a\)
- \(12⋅x⋅x⋅y⋅y⋅y⋅y⋅y⋅y\)
- \(−6⋅(x−1)(x−1)(x−1)\)
- \((9ab)(9ab)(9ab)(a^{2}−b)(a^{2}−b)\)
- Answer
-
1. \((2x)^{5}\)
3. \(-10a^{7}\)
5. \(-6(x-1)^{3}\)
Exercise \(\PageIndex{5}\) Product, Quotient, and Power Rule for Exponents
Simplify.
- \(2^{7}⋅2^{5}\)
- \(3^{9}⋅3\)
- \(−2^{4}\)
- \((−2)^{4}\)
- \(−3^{3}\)
- \((−3)^{4}\)
- \(10^{13}⋅10^{5}⋅10^{4}\)
- \(10^{8}⋅10^{7}⋅10\)
- \(\frac{5^{12}}{5^{2}}\)
- \(\frac{10^{7}}{10^{10}}\)
- \(\frac{10^{12}}{10^{9}}\)
- \((7^{3})^{^{5}}\)
- \((4^{8})^{^{4}}\)
- \(10^{6}⋅(10^{5})^{^{4}}\)
- Answer
-
1. \(2^{12}\)
3. \(−16\)
5. \(−27\)
7. \(10^{22}\)
9. \(5^{10}\)
11. \(10^{3}\)
13. \(4^{32}\)
Exercise \(\PageIndex{6}\) Product, Quotient, and Power Rule for Exponents
Simplify.
- \((−x)^{6}\)
- \(a^{5}⋅(−a)^{2}\)
- \(x^{3}⋅x^{5}⋅x\)
- \(y^{5}⋅y^{4}⋅y^{2}\)
- \((a^{5})^{^{2}}⋅(a^{3})^{^{4}}⋅a\)
- \((x+1)^{4}(y^{5})^{^{4}}⋅y^{2}\)
- \((x+1)^{5}(x+1)^{8}\)
- \((2a−b)^{12}(2a−b)^{9}\)
- \(\frac{(3x-1)^{5}}{(3x-1)^{2}}\)
- \(\frac{(a-5)^{37}}{(a-5)^{13}}\)
- \(xy^{2}⋅x^{2}y\)
- \(3x^{2}y^{3}⋅7xy^{5}\)
- \(−8a^{2}b⋅2ab\)
- \(−3ab^{2}c^{3}⋅9a^{4}b^{5}c^{6}\)
- \(2a^{2}b^{4}c (−3abc)\)
- \(5a^{2}(b^{3})^{^{3}}c^{3}⋅(−2)2a^{3}(b^{2})^{^{4}}\)
- \(2x^{2}(x+y)^{5}⋅3x^{5}(x+y)^{4}\)
- \(−5xy^{6}(2x−1)^{6}⋅x^{5}y(2x−1)^{3}\)
- \(x^{2}y⋅xy^{3}⋅x^{5}y^{5}\)
- \(−2x^{10}y⋅3x^{2}y^{12}⋅5xy^{3}\)
- \(3^{2}x^{4}y^{2}z⋅3xy^{4}z^{4}\)
- \((−x^{2})^{^{3}}(x^{3})^{^{2}}(x^{4})^{^{3}}\)
- \(a^{10}⋅\frac{(a^{6})^{^{3}}}{a^{3}}\)
- \(\frac{10x^{9}(x^{3})^{^{5}}}{2x^{5}}\)
- \(\frac{a^{6}b^{3}}{a^{2}b^{2}}\)
- \(\frac{m^{10}n^{7}}{m^{3}n^{4}}\)
- \(\frac{20x^{5}y^{12}z^{3}}{10x^{2}y^{10}z}\)
- \(\frac{-24a^{16}b^{12}c^{3}}{6a^{6}b^{11}c}\)
- \(\frac{16x^{4}(x+2)^{3}}{4x(x+2)}\)
- \(\frac{50y^{2}(x+y)^{20}}{10y(x+y)^{17}}\)
- Answer
-
1. \(x^{6}\)
3. \(x^{9}\)
5. \(a^{23}\)
7. \((x+1)^{13}\)
9. \((3x−1)^{3}\)
11. \(x^{3}y^{3}\)
13. \(−16a^{3}b^{2}\)
15. \(−6a^{3}b^{5}c^{2}\)
17. \(6x^{7}(x+y)^{9}\)
19. \(x^{8}y^{9}\)
21. \(27x^{5}y^{6}z^{5}\)
23. \(a^{25}\)
25. \(a^{4}b\)
27. \(2x^{3}y^{2}z^{2}\)
29. \(4x^{3}(x+2)^{2}\)
Exercise \(\PageIndex{7}\) Power Rules for Products and Quotients
Simplify.
- \((2x)^{5}\)
- \((−3y)^{4}\)
- \((−xy)^{3}\)
- \((5xy)^{3}\)
- \((−4abc)^{2}\)
- \(\left(\frac{7}{2x} \right)^{2}\)
- \(-\left(\frac{5}{3y} \right)^{3}\)
- \((3abc)^{3}\)
- \(\left(\frac{-2xy}{3z} \right)^{4}\)
- \(\left(\frac{5y}{(2x-1)x}\right)^{3}\)
- \((3x^{2})^{^{3}}\)
- \((−2x^{3})^{^{2}}\)
- \((xy^{5})^{^{7}}\)
- \((x^{2}y^{10})^{^{2}}\)
- \(\left(\frac{3x^{2}}{y} \right)^{3}\)
- \((2x^{2}y^{3}z^{4})^{^{5}}\)
- \(\left(\frac{-7ab^{4}}{c^{2}} \right)^{2}\)
- \([x^{5}y^{4}(x+y)^{4}]^{5}\)
- \([2y(x+1)^{5}]^{3}\)
- \((ab^{3})^{^{3}}\)
- \(\left(\frac{5a^{2}}{3b} \right)^{4}\)
- \(\left(\frac{-2x^{3}}{3y^{2}} \right)^{2}\)
- \(\left(\frac{-x^{2}}{y^{3}} \right)^{3}\)
- \(\left(\frac{ab^{2}}{3c^{3}d^{2}} \right)^{4}\)
- \(\left(\frac{2x^{7}y}{(x-1)^{3}z^{5}} \right)^{6}\)
- \((2x^{4})^{^{3}}⋅(x^{5})^{^{2}}\)
- \((x^{3}y)^{^{2}}⋅(xy^{4})^{^{3}}\)
- \((−2a^{2}b^{3})^{^{2}}⋅(2a^{5}b)^{^{4}}\)
- \((−a^{2}b)^{3}(3ab^{4})^{4}\)
- \((2x^{3}(x+y)^{4})^{5}⋅(2x^{4}(x+y)^{2})^{3}\)
- \(\left(\frac{-3x^{5}y^{4}}{xy^{2}} \right)^{3}\)
- \(\left(\frac{-3x^{5}y^{4}}{xy^{2}} \right)^{2}\)
- \(\left(\frac{-25x^{10}y^{15}}{5x^{5}y^{10}} \right)^{3}\)
- \(\left(\frac{10x^{3}y^{5}}{5xy^{2}} \right)^{2}\)
- \(\left(\frac{-24ab^{3}}{6bc} \right)^{5}\)
- \(\left(\frac{-2x^{3}y^{16}}{x^{2}y} \right)^{2}\)
- \(\left(\frac{30ab^{3}}{3abc} \right)^{3}\)
- \(\left(\frac{3s^{3}t^{2}}{2s^{2}t} \right)^{3}\)
- \(\left(\frac{6xy^{5}(x+y)^{6}}{3y^{2}z(x+y)^{2}} \right)^{5}\)
- \(\left(\frac{-64a^{5}b^{12}c^{2}(2ab-1)^{14}}{32a^{2}b^{10}c^{2}(2ab-1)^{7}} \right)^{4}\)
- The probability of tossing a fair coin and obtaining \(n\) heads in a row is given by the formula \(P=(12)^{n}\). Determine the probability, as a percent, of tossing \(5\) heads in a row.
- The probability of rolling a single fair six-sided die and obtaining \(n\) of the same faces up in a row is given by the formula \(P=(16)^{n}\). Determine the probability, as a percent, of obtaining the same face up two times in a row.
- If each side of a square measures \(2x^{3}\) units, then determine the area in terms of the variable \(x\).
- If each edge of a cube measures \(5x^{2}\) units, then determine the volume in terms of the variable \(x\).
- Answer
-
1. \(32x^{5}\)
3. \(−x^{3}y^{3}\)
5. \(16a^{2}b^{2}c^{2}\)
7. \(−\frac{125}{27y^{3}}\)
9. \(\frac{16x^{4}y^{4}}{81z^{4}}\)
11. \(27x^{6}\)
13. \(x^{7}y^{35}\)
15. \(\frac{27x^{6}}{y^{3}}\)
17. \(\frac{49a^{2}b^{8}}{c^{4}}\)
19. \(8y^{3}(x+1)^{15}\)
21. \(\frac{625a^{8}}{81b^{4}}\)
23. \(−\frac{x^{6}}{y^{9}}\)
25. \(\frac{64x^{42}y^{6}}{(x−1)^{18}z^{30}}\)
27. \(x^{9}y^{14}\)
29. \(−81a^{10}b^{19}\)
31. \(−27x^{12}y^{6}\)
33. \(−125x^{15}y^{15}\)
35. \(\frac{−1024a^{5}b^{10}}{c^{5}}\)
37. \(\frac{1000b^{6}}{c^{3}}\)
39. \(\frac{32x^{5}y^{15}(x+y)^{20}}{z^{5}}\)
41. \(3 \frac{1}{8}\)%
43. \(A=4x^{6}\)
Exercise \(\PageIndex{8}\) Zero Exponents
Simplify. (Assume variables are nonzero.)
- \(7^{0}\)
- \((−7)^{0}\)
- \(−10^{0}\)
- \(−3^{0}⋅(−7)^{0}\)
- \(8675309^{0}\)
- \(5^{2}⋅3^{0}⋅2^{3}\)
- \(−3^{0}⋅(−2)^{2}⋅(−3)^{0}\)
- \(\frac{5x^{0}}{y^{2}}\)
- \((−3)^{2}x^{2}y^{0}z^{5}\)
- \(−3^{2}(x^{3})^{2}y^{2}(z^{3})^{0}\)
- \(2x^{3}y^{0}z⋅3x^{0}y^{3}z^{5}\)
- \(−3ab^{2}c^{0}⋅3a^{2}(b^{3}c^{2})^{0}\)
- \((−8xy^{2})^{0}\)
- \((2x^{2}y^{3})^{0}\)
- \(\frac{9x^{0}y^{4}}{3y^{3}}\)
- Answer
-
1. \(1\)
3. \(−1\)
5. \(1\)
7. \(−4\)
9. \(9x^{2}z^{5}\)
11. \(6x^{3}y^{3}z^{6}\)
13. \(1\)
15. \(3y\)
Exercise \(\PageIndex{9}\) Discussion Board Topics
- René Descartes (1637) established the usage of exponential form: \(a^{2}, a^{3}\), and so on. Before this, how were exponents denoted?
- Discuss the accomplishments accredited to Al-Karismi.
- Why is \(0^{0}\) undefined?
- Explain to a beginning student why \(3^{4}⋅3^{2}≠9^{6}\).
- Answer
-
1. Answers may vary
3. Answers may vary


