6.7: Applications Involving Quadratic Equations
- Page ID
- 23744
Learning Objectives
- Set up and solve applications involving relationships between real numbers.
- Set up and solve applications involving geometric relationships involving area and the Pythagorean theorem.
- Set up and solve applications involving the height of projectiles.
Number Problems
The algebraic setups of the word problems that we have previously encountered led to linear equations. When we translate the applications to algebraic setups in this section, the setups lead to quadratic equations. Just as before, we want to avoid relying on the “guess and check” method for solving applications. Using algebra to solve problems simplifies the process and is more reliable.
Example \(\PageIndex{1}\)
One integer is \(4\) less than twice another integer, and their product is \(96\). Set up an algebraic equation and solve it to find the two integers.
Solution:
First, identify the variables. Avoid two variables by using the relationship between the two unknowns.
.png?revision=1)
The key phrase, “their product is \(96\),” indicates that we should multiply and set the product equal to \(96\).
\(n\cdot (2n-4)=96\)
Once we have the problem translated to a mathematical equation, we then solve. In this case, we can solve by factoring. The first step is to write the equation in standard form:
\(\begin{array} {cc} {n\cdot (2n-4)=96}&{\color{Cerulean}{Distribute\:n.}}\\{2n^{2}-4n=96}&{\color{Cerulean}{Subtract\:96\:from\:both\:sides.}}\\{2n^{2}-4n-96=0}&{} \end{array}\)
Next, factor completely and set each variable factor equal to zero.
\(\begin{array}{cc}{2n^{2}-4n-96=0}&{\color{Cerulean}{Factor\:out\:the\:GCF,\:2.}}\\{2(n^{2}-2n-48)=0}&{\color{Cerulean}{Factor\:the\:resulting\:trinomial.}}\\{2(n+6)(n-8)=0}&{\color{Cerulean}{Set\:each\:variable\:factor\:equal\:to\:zero.}} \end{array}\)
\(\begin{array}{ccc}{n+6=0}&{\text{or}}&{n-8=0}\\{n=-6}&{}&{n=8} \end{array}\)
The problem calls for two integers whose product is \(+96\). The product of two positive numbers is positive and the product of two negative numbers is positive. Hence we can have two sets of solutions. Use \(2n−4\) to determine the other integers.
\(\begin{array} {cc} {n=-6}&{n=8}\\{2n-4=2(\color{OliveGreen}{-6}\color{black}{)-4}}&{2n-4=2(\color{OliveGreen}{8}\color{black}{)-4}}\\{=-12-4}&{=16-4}\\{=-16}&{=12} \end{array}\)
Answer:
Two sets of integers solve this problem: {\(8, 12\)} and {\(−6, −16\)}. Notice that \((8)(12) = 96\) and \((−6)(−16) = 96\); our solutions check out.
With quadratic equations, we often obtain two solutions for the identified unknown. Although it may be the case that both are solutions to the equation, they may not be solutions to the problem. If a solution does not solve the original application, then we disregard it.
Recall that consecutive odd and even integers both are separated by two units.
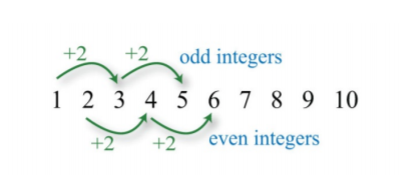.png?revision=1)
Example \(\PageIndex{2}\)
The product of two consecutive positive odd integers is \(99\). Find the integers.
Solution:
Let \(n\) represent the first positive odd integer.
Let \(\color{OliveGreen}{n+2}\) represent the next positive odd integer.
The key phase, “product…is 99,” indicates that we should multiply and set the product equal to \(99\).
\(n\cdot (n+2)=99\)
Rewrite the quadratic equation in standard form and solve by factoring.
\(\begin{aligned} n^{2}+2n&=99 \\ n^{2}+2n-99&=0 \\ (n-9)(n+11)&=0 \end{aligned}\)
\(\begin{array}{ccc}{n-9=0}&{\text{or}}&{n+11=0}\\{n=9}&{}&{n=-11} \end{array}\)
Because the problem asks for positive integers, \(n=9\) is the only solution. Back substitute to determine the next odd integer.
\(\begin{aligned} n+2&=\color{OliveGreen}{9}\color{black}{+2} \\ &=11 \end{aligned}\)
Answer:
The consecutive positive odd integers are \(9\) and \(11\).
Example \(\PageIndex{3}\)
Given two consecutive positive odd integers, the product of the larger and twice the smaller is equal to \(70\). Find the integers.
Solution:
Let \(n\) represent the smaller positive odd integer.
Let \(n+2\) represent the next positive odd integer.
The key phrase “twice the smaller” can be translated to \(2n\). The phrase “product…is 70” indicates that we should multiply this by the larger odd integer and set the product equal to \(70\).
\((n+2)\cdot 2n=70\)
Solve by factoring.
\(\begin{array}{cc}{(n+2)\cdot 2n=70}&{\color{Cerulean}{Distribute.}}\\{2n^{2}+4n=70}&{\color{Cerulean}{Subtract\:70\:from\:both\:sides.}}\\{2n^{2}+4n-70=0}&{\color{Cerulean}{Factor\:out\:the\:GCF,\:2.}}\\{2(n^{2}+2n-35)=0}&{\color{Cerulean}{Factor\:the\:resulting\:trinomial.}}\\{2(n-5)(n+7)=0}&{\color{Cerulean}{Set\:each\:variable\:factor\:equal\:to\:zero.}} \end{array}\)
\(\begin{array}{ccc}{n-5=0}&{\text{or}}&{n+7=0}\\{n=5}&{}&{n=-7} \end{array}\)
Because the problem asks for positive integers, \(n=5\) is the only solution.
Back substitute into \(n + 2\) to determine the next odd integer.
\(\begin{aligned} n+2&=\color{OliveGreen}{5}\color{black}{+2}\\&=7 \end{aligned}\)
Answer:
The positive odd integers are \(5\) and \(7\).
Exercise \(\PageIndex{1}\)
The product of two consecutive positive even integers is \(168\). Find the integers.
- Answer
-
The positive even integers are \(12\) and \(14\).
Geometry Problems
When working with geometry problems, it is helpful to draw a picture. Below are some area formulas that you are expected to know. (Recall that \(π≈3.14\).)
| Area of a rectangle: | \(A=l\cdot w\) |
| Area of a square: | \(A=s^{2}\) |
| Area of a triangle: | \(A=\frac{1}{2}bh\) |
| Area of a circle: | \(A=\pi r^{2}\) |
Example \(\PageIndex{4}\)
The floor of a rectangular room has a length that is \(4\) feet more than twice its width. If the total area of the floor is \(240\) square feet, then find the dimensions of the floor.
Solution:
.png?revision=1)
Use the formula \(A=l⋅w\) and the fact that the area is \(240\) square feet to set up an algebraic equation.
\(\begin{aligned} A&=l\cdot w \\ \color{OliveGreen}{240}&\color{black}{=(}\color{OliveGreen}{2w+4}\color{black}{)\cdot w} \end{aligned}\)
Solve by factoring.
\(\begin{array} {ccc} {w-10=0}&{\text{or}}&{w+12=0} \\{w=10}&{}&{w=-12} \end{array}\)
At this point we have two possibilities for the width of the rectangle. However, since a negative width is not defined, choose the positive solution, \(w=10\). Back substitute to find the length.
\(\begin{aligned} 2w+4&=2(\color{OliveGreen}{10}\color{black}{)+4} \\ &=20+4 \\ &=24 \end{aligned}\)
Answer:
The width is \(10\) feet and the length is \(24\) feet.
It is important to include the correct units in the final presentation of the answer. In the previous example, it would not make much sense to say the width is \(10\). Make sure to indicate that the width is \(10\) feet.
Example \(\PageIndex{5}\)
The height of a triangle is \(3\) inches less than twice the length of its base. If the total area of the triangle is \(7\) square inches, then find the lengths of the base and height.
Solution:
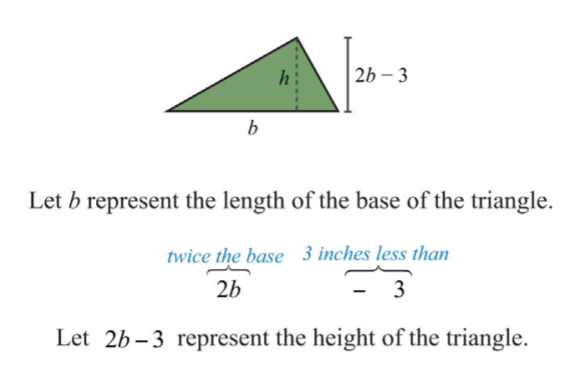.png?revision=1)
Use the formula \(A=\frac{1}{2}bh\) and the fact that the area is \(7\) square inches to set up an algebraic equation.
\(\begin{aligned} A&=\frac{1}{2} b\cdot h \\ \color{OliveGreen}{7}&\color{black}{=\frac{1}{2}b(\color{OliveGreen}{2b-3}\color{black}{)}} \end{aligned}\)
To avoid fractional coefficients, multiply both sides by \(2\) and then rewrite the quadratic equation in standard form.
Factor and then set each factor equal to zero.
\(\begin{array}{ccc}{2b-7=0}&{\text{or}}&{b+2=0}\\{2b=7}&{}&{b=-2}\\{b=\frac{7}{2}}&{}&{} \end{array}\)
In this case, disregard the negative answer; the length of the base is \(\frac{7}{2}\) inches long. Use \(2b−3\) to determine the height of the triangle.
Answer:
The base measures \(\frac{7}{2} = 3\frac{1}{2}\) inches and the height is \(4\) inches.
Exercise \(\PageIndex{1}\)
The base of a triangle is \(5\) units less than twice the height. If the area is \(75\) square units, then what is the length of the base and height?
- Answer
-
The height is \(10\) units and the base is \(15\) units.
Recall that a right triangle is a triangle where one of the angles measures \(90\)°. The side opposite of the right angle is the longest side of the triangle and is called the hypotenuse. The Pythagorean theorem gives us a relationship between the legs and hypotenuse of any right triangle, where \(a\) and \(b\) are the lengths of the legs and \(c\) is the length of the hypotenuse:
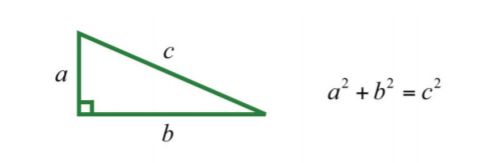.png?revision=1)
Given certain relationships, we use this theorem when determining the lengths of sides of right triangles.
Example \(\PageIndex{6}\)
The hypotenuse of a right triangle is \(10\) inches. If the short leg is \(2\) inches less than the long leg, then find the lengths of the legs.
Solution:
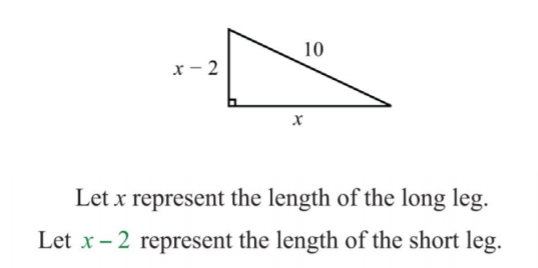.png?revision=1)
Given that the hypotenuse measures \(10\) inches, substitute its value into the Pythagorean theorem and obtain a quadratic equation in terms of \(x\).
\(\begin{aligned} a^{2}+b^{2}&=c^{2} \\ (\color{OliveGreen}{x-2}\color{black}{)^{2}+}\color{OliveGreen}{x}\color{black}{^{2}}&=\color{OliveGreen}{10}\color{black}{^{2}} \end{aligned}\)
Multiply and rewrite the equation in standard form.
\(\begin{aligned} (x-2)^{2}+x^{2}&=10^{2} \\ x^{2}-4x+4+x^{2}&=100 \\ 2x^{2}-4x-96&=0 \end{aligned}\)
Once it is in standard form, factor and set each variable factor equal to zero.
\(\begin{aligned} 2x^{2}-4x-96&=0\\ 2(x^{2}-2x-48)&=0 \\ 2(x+6)(x-8)&=0 \end{aligned}\)
\(\begin{array}{ccc}{x+6=0}&{\text{or}}&{x-8=0}\\{x=-6}&{}&{x=8} \end{array}\)
Because lengths cannot be negative, disregard the negative answer. In this case, the long leg measures \(8\) inches. Use \(x−2\) to determine the length of the short leg.
\(\begin{aligned} x-2&=\color{OliveGreen}{8}\color{black}{-2} \\ &=6 \end{aligned}\)
Answer:
The short leg measures \(6\) inches and the long leg measures \(8\) inches.
Example \(\PageIndex{7}\)
One leg of a right triangle measures \(3\) centimeters. The hypotenuse of the right triangle measures \(3\) centimeters less than twice the length of the unknown leg. Find the measure of all the sides of the triangle.
Solution:
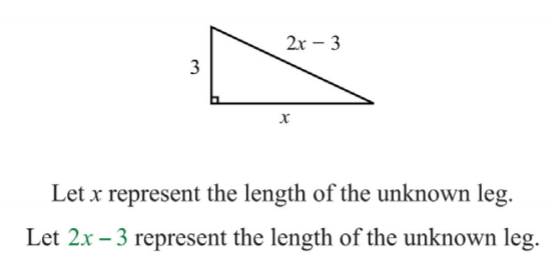.png?revision=1)
To set up an algebraic equation, we use the Pythagorean theorem.
\(\begin{aligned} a^{2}+b^{2}&=c^{2} \\ \color{OliveGreen}{3}\color{black}{^{2}+}\color{OliveGreen}{x}\color{black}{^{2}}&=(\color{OliveGreen}{2x-3}\color{black}{)^{2}} \end{aligned}\)
Solve by factoring.
\(\begin{aligned} 3^{2}+x^{2}&=(2x-3)^{2} \\ 9+x^{2}&=4x^{2}-12x+9 \\ 0&=3x^{2}-12x \\ 0&=3x(x-4) \end{aligned}\)
\(\begin{array}{ccc}{3x=0}&{\text{or}}&{x-4=0}\\{x=0}&{}&{x=4} \end{array}\)
Disregard \(0\). The length of the unknown leg is \(4\) centimeters. Use \(2x−3\) to determine the length of the hypotenuse.
Answer:
The sides of the triangle measure \(3\) centimeters, \(4\) centimeters, and \(5\) centimeters.
Exercise \(\PageIndex{2}\)
The hypotenuse of a right triangle measures \(13\) units. If one leg is \(2\) units more than twice that of the other, then find the length of each leg.
- Answer
-
The two legs measure \(5\) units and \(12\) units.
Projectile Problems
The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following formula:
\[\text{height}=-\frac{1}{2}gt^{2}+v_{0}t+s_{0}\]
Using function notation, which is more appropriate, we have
\[h(t)=-\frac{1}{2}gt^{2}+v_{0}t+s_{0}\]
With this formula, the height can be calculated at any given time \(t\) after the object is launched. The coefficients represent the following:
| \(-\frac{1}{2}g\) | The letter \(g\) represents the acceleration due to gravity. |
| \(v_{0}\) | “\(v\)-naught” represents the initial velocity of the object. |
| \(s_{0}\) | “\(s\)-naught” represents the initial height from which the object is launched. |
We consider only problems where the acceleration due to gravity can be expressed as \(g=32\) ft/sec\(^{2}\). Therefore, in this section time will be measured in seconds and the height in feet. Certainly though, the formula is valid using units other than these.
Example \(\PageIndex{8}\)
The height of a projectile launched upward at a speed of \(32\) feet/second from a height of \(128\) feet is given by the function \(h(t)=−16t^{2}+32t+128\). How long does it take to hit the ground?
Solution:
An inefficient method for finding the time to hit the ground is to simply start guessing at times and evaluating. To do this, construct a chart.
.png?revision=1)
Use the table to sketch the height of the projectile over time.
.png?revision=1)
We see that at \(4\) seconds, the projectile hits the ground. Note that when this occurs, the height is equal to \(0\). Now we need to solve this problem algebraically. To find the solution algebraically, use the fact that the height is \(0\) when the object hits the ground. We need to find the time, \(t\), when \(h(t)=0\).
\(h(t)=-16t^{2}+32t+128 \\ \color{Cerulean}{\downarrow} \\ 0 =-16t^{2}+32t+128\)
Solve the equation by factoring
\(\begin{aligned} 0 &=-16t^{2}+32t+128 \\ 0 &=-16(t^{2}-2t-8) \\ 0&=-16(t-4)(t+2) \end{aligned}\)
Now set each variable factor to zero.
\(\begin{array}{ccc}{t-4=0}&{\text{or}}&{t+2=0}\\{t=4}&{}&{t=-2} \end{array}\)
As expected, the projectile hits the ground at \(t=4\) seconds. Disregard \(−2\) as a solution because negative time is not defined.
Answer:
The projectile hits the ground \(4\) seconds after it is launched.
Example \(\PageIndex{9}\)
The height of a certain book dropped from the top of a \(144\) foot building is given by \(h(t)=−16t^{2}+144\). How long does it take to hit the ground?
Solution:
Find the time \(t\) when the height \(h(t)=0\).
\(\begin{aligned}0&=-16t^{2}+144 \\ 0&=-16(t^{2}-9) \\ 0&=-16(t+3)(t-3) \end{aligned}\)
\(\begin{array}{ccc}{t+3=0}&{\text{or}}&{t-3=0}\\{t=-3}&{}&{t=3} \end{array}\)
Answer:
The book takes \(3\) seconds to hit the ground when dropped from the top of a \(144\)-foot building.
Exercise \(\PageIndex{3}\)
The height of a projectile, shot straight up into the air from the ground, is given by \(h(t)=−16t^{2}+80t\). How long does it take to come back down to the ground?
- Answer
-
It will take 5 seconds to come back down to the ground.
Key Takeaways
- It is best to translate a word problem to a mathematical setup and then solve using algebra. Avoid using the “guess and check” method of solving applications in this section.
- When solving applications, check that your solutions make sense in the context of the question. For example, if you wish to find the length of the base of a triangle, then you would disregard any negative solutions.
- It is important to identify each variable and state in a sentence what each variable represents. It is often helpful to draw a picture.
Exercise \(\PageIndex{4}\) Number Problems
Set up an algebraic equation and then solve.
- One integer is five times another. If the product of the two integers is \(80\), then find the integers.
- One integer is four times another. If the product of the two integers is \(36\), then find the integers.
- An integer is one more than four times another. If the product of the two integers is \(39\), then find the integers.
- An integer is \(3\) more than another. If the product of the two integers is \(130\), then find the integers.
- An integer is \(2\) less than twice another. If the product of the two integers is \(220\), then find the integers.
- An integer is \(3\) more than twice another. If the product of the two integers is \(90\), then find the integers.
- One integer is \(2\) units more than another. If the product of the two integers is equal to five times the larger, then find the two integers.
- A positive integer is \(1\) less than twice another. If the product of the two integers is equal to fifteen times the smaller, then find the two integers.
- A positive integer is \(3\) more than twice a smaller positive integer. If the product of the two integers is equal to six times the larger, then find the integers.
- One positive integer is \(3\) more than another. If the product of the two integers is equal to twelve times the smaller, then find the integers.
- An integer is \(3\) more than another. If the product of the two integers is equal to \(2\) more than four times their sum, then find the integers.
- An integer is \(5\) more than another. If the product of the two integers is equal to \(2\) more than twice their sum, then find the integers.
- The product of two consecutive positive even integers is \(120\). Find the integers.
- The product of two consecutive positive odd integers is \(99\). Find the integers.
- The product of two consecutive positive integers is \(110\). Find the integers.
- The product of two consecutive positive integers is \(42\). Find the integers.
- The product of two consecutive positive odd integers is equal to \(1\) less than seven times the sum of the integers. Find the integers.
- The product of two consecutive positive even integers is equal to \(22\) more than eleven times the sum of the integers. Find the integers.
- The sum of the squares of two consecutive positive odd integers is \(74\). Find the integers.
- The sum of the squares of two consecutive positive even integers is \(100\). Find the integers.
- The sum of the squares of two consecutive positive integers is \(265\). Find the integers.
- The sum of the squares of two consecutive positive integers is \(181\). Find the integers.
- For two consecutive positive odd integers, the product of twice the smaller and the larger is \(126\). Find the integers.
- For two consecutive positive even integers, the product of the smaller and twice the larger is \(160\). Find the integers.
- Answer
-
1. {\(4, 20\)} or {\(−4, −20\)}
3. \(3, 13\)
5. {\(11, 20\)} or {\(−22, −10\)}
7. {\(5, 7\)} or {\(−2, 0\)}
9. \(6, 15\)
11. {\(7, 10\)} or {\(−2, 1\)}
13. \(10, 12\)
15. \(10, 11\)
17. \(13, 15\)
19. \(5, 7\)
21. \(11, 12\)
23. \(7, 9\)
Exercise \(\PageIndex{5}\) Geometry Problems
Set up an algebraic equation and then solve.
- The width of a rectangle is \(7\) feet less than its length. If the area of the rectangle is \(170\) square feet, then find the length and width.
- The length of a rectangle is \(2\) feet more than its width. If the area of the rectangle is \(48\) square feet, then find the length and width.
- The width of a rectangle is \(3\) units less than the length. If the area is \(70\) square units, then find the dimensions of the rectangle.
- The width of a rectangle measures one half of the length. If the area is \(72\) square feet, then find the dimensions of the rectangle.
- The length of a rectangle is twice that of its width. If the area of the rectangle is \(72\) square inches, then find the length and width.
- The length of a rectangle is three times that of its width. If the area of the rectangle is \(75\) square centimeters, then find the length and width.
- The length of a rectangle is \(2\) inches more than its width. The area of the rectangle is equal to \(12\) inches more than three times the perimeter. Find the length and width of the rectangle.
- The length of a rectangle is \(3\) meters more than twice the width. The area of the rectangle is equal to \(10\) meters less than three times the perimeter. Find the length and width of the rectangle.
- A uniform border is to be placed around an \(8\)-inch-by-\(10\)-inch picture. If the total area including the border must be \(224\) square inches, then how wide should the border be?
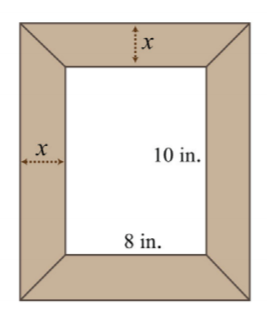.png?revision=1)
10. A \(2\)-foot brick border is constructed around a square cement slab. If the total area, including the border, is \(121\) square feet, then what are the dimensions of the slab?
11. The area of a picture frame including a \(2\)-inch wide border is \(99\) square inches. If the width of the inner area is \(2\) inches more than its length, then find the dimensions of the inner area.
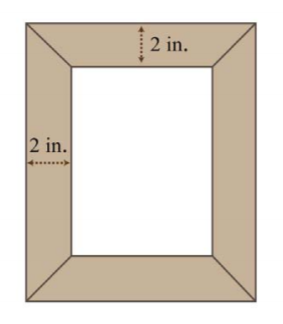.png?revision=1)
12. A box can be made by cutting out the corners and folding up the edges of a square sheet of cardboard. A template for a cardboard box with a height of \(2\) inches is given. What is the length of each side of the cardboard sheet if the volume of the box is to be \(50\) cubic inches?
.png?revision=1)
13. The height of a triangle is \(3\) inches more than the length of its base. If the area of the triangle is \(44\) square inches, then find the length of its base and height.
14. The height of a triangle is \(4\) units less than the length of the base. If the area of the triangle is \(48\) square units, then find the length of its base and height.
15. The base of a triangle is twice that of its height. If the area is \(36\) square centimeters, then find the length of its base and height.
16. The height of a triangle is three times the length of its base. If the area is \(73\frac{1}{2}\) square feet, then find the length of the base and height.
17. The height of a triangle is \(1\) unit more than the length of its base. If the area is \(5\) units more than four times the height, then find the length of the base and height of the triangle.
18. The base of a triangle is \(4\) times that of its height. If the area is \(3\) units more than five times the height, then find the length of the base and height of the triangle.
19. The diagonal of a rectangle measures \(5\) inches. If the length is \(1\) inch more than its width, then find the dimensions of the rectangle.
20. The diagonal of a rectangle measures \(10\) inches. If the width is \(2\) inches less than the length, then find the area of the rectangle.
21. If the sides of a right triangle are consecutive even integers, then what are their measures?
22. The hypotenuse of a right triangle is \(13\) units. If the length of one leg is \(2\) more than twice the other, then what are their lengths?
23. The shortest leg of a right triangle measures \(9\) centimeters and the hypotenuse measures \(3\) centimeters more than the longer leg. Find the length of the hypotenuse.
24. The long leg of a right triangle measures \(24\) centimeters and the hypotenuse measures \(4\) centimeters more three times the short leg. Find the length of the hypotenuse.
- Answer
-
1. Length: \(17\) feet; width: \(10\) feet
3. Length: \(10\) units; width: \(7\) units
5. Length: \(12\) inches; width: \(6\) inches
7. Length: \(14\) inches; width: \(12\) inches
9. \(3\) inches
11. \(5\) inches by \(7\) inches
13. Base: \(8\) inches; height: \(11\) inches
15. Base: \(12\) centimeters; height: \(6\) centimeters
17. Base: \(9\) units; height: \(10\) units
19. \(3\) inches by \(4\) inches
21. \(6\) units, \(8\) units, and \(10\) units
23. \(15\) centimeters
Exercise \(\PageIndex{6}\) Projectile Problems
Set up an algebraic equation and then solve.
- The height of a projectile launched upward at a speed of \(32\) feet/second from a height of \(48\) feet is given by the function \(h(t)=−16t^{2}+32t+48. How long will it take the projectile to hit the ground?
- The height of a projectile launched upward at a speed of \(16\) feet/second from a height of \(192\) feet is given by the function \(h(t)=−16t^{2}+16t+192\). How long will it take to hit the ground?
- An object launched upward at a speed of \(64\) feet/second from a height of \(80\) feet. How long will it take the projectile to hit the ground?
- An object launched upward at a speed of \(128\) feet/second from a height of \(144\) feet. How long will it take the projectile to hit the ground?
- The height of an object dropped from the top of a \(64\)-foot building is given by \(h(t)=−16t^{2}+64\). How long will it take the object to hit the ground?
- The height of an object dropped from an airplane at \(1,600\) feet is given by \(h(t)=−16t^{2}+1,600\). How long will it take the object to hit the ground?
- An object is dropped from a ladder at a height of \(16\) feet. How long will it take to hit the ground?
- An object is dropped from a \(144\)-foot building. How long will it take to hit the ground?
- The height of a projectile, shot straight up into the air from the ground at \(128\) feet/second, is given by \(h(t)=−16t^{2}+128t\). How long does it take to come back down to the ground?
- A baseball, tossed up into the air from the ground at \(32\) feet/second, is given by \(h(t)=−16t^{2}+32t\). How long does it take to come back down to the ground?
- How long will it take a baseball thrown into the air at \(48\) feet/second to come back down to the ground?
- A football is kicked up into the air at \(80\) feet/second. Calculate how long will it hang in the air.
- Answer
-
1. \(3\) seconds
3. \(5\) seconds
5. \(2\) seconds
7. \(1\) second
9. \(8\) seconds
11. \(3\) seconds
Exercise \(\PageIndex{7}\) Discussion Board Topics
- Research and discuss the life of Pythagoras.
- If the sides of a square are doubled, then by what factor is the area increased? Why?
- Design your own geometry problem involving the area of a rectangle or triangle. Post the question and a complete solution on the discussion board.
- Write down your strategy for setting up and solving word problems. Share your strategy on the discussion board.
- Answer
-
1. Answers may vary
3. Answers may vary


