1.3: The Rational Numbers

We begin with the definition of a rational number.

Rational Numbers

Any number that can be expressed in the form \(p/q\), where \(p\) and \(q\) are integers, \(q \neq 0\), is called a rational number. The letter \(\mathbb{Q}\) is used to represent the set of rational numbers. That is:

\[\mathbb{Q}=\left\{\dfrac{p}{q} : p \text { and } q \text { are integers, } q \neq 0\right\} \nonumber \]

Because \(-2/3\), \(4/5\), and \(123/(-12)\) have the form \(p/q\), where \(p\) and \(q\) are integers, each is an example of a rational number. If you think you hear the word “fraction” when we say “rational number,” you are correct in your thinking. Any number that can be expressed as a fraction, where the numerator and denominator are integers, is a rational number. Every integer is also a rational number. Take, for example, the integer \(-12\). There are a number of ways we can express \(-12\) as a fraction with integer numerator and denominator, \(-12/1\), \(24/(-2)\), and \(-36/3\) being a few.

Reducing Fractions to Lowest Terms

First, we define what is meant by the greatest common divisor of two integers.

The Greatest Common Divisor

Given two integers \(a\) and \(b\), the greatest common divisor of \(a\) and \(b\) is the largest integer that divides evenly (with no remainder) into both \(a\) and \(b\). The notation \(\operatorname{GCD}(a, b)\) is used to represent the greatest common divisor of \(a\) and \(b\).

For example, \(\operatorname{GCD}(12,18)=6, \operatorname{GCD}(32,40)=8,\) and \(\operatorname{GCD}(18,27)=9\).

We can now state when a fraction is reduced to lowest terms.

Lowest Terms

A fraction \(a/b\) is said to be reduced to lowest terms if and only if \(\operatorname{GCD}(a, b)=1\).

A common technique used to reduce a fraction to lowest terms is to divide both numerator and denominator by their greatest common divisor.

Example \(\PageIndex{1}\)

Reduce \(8/12\) to lowest terms.

Solution

Note that \(\operatorname{GCD}(8,12)=4\). Divide both numerator and denominator by \(4\).

\[\begin{aligned} \dfrac{8}{12} &=\dfrac{8 \div 4}{12 \div 4} \quad \color{Red} \text{Divide numerator and denominator by } \operatorname{GCD}(8,12)=4 \\ &=\dfrac{2}{3} \quad \color{Red} \text{Simplify numerator and denominator.}\\ \text{Thus, } 8/12 &= 2/3 \end{aligned} \nonumber\]

Exercise \(\PageIndex{1}\)

Reduce: \(-48 / 60\).

Answer

\(-4 / 5\)

Recall the definition of a prime number.

Prime Number

A natural number greater than one is prime if and only if its only divisors are one and itself.

For example, \(7\) is prime (its only divisors are \(1\) and \(7\)), but \(14\) is not (its divisors are \(1\), \(2\), \(7\), and \(14\)). In like fashion, \(2\), \(3\), and \(5\) are prime, but \(6\), \(15\), and \(21\) are not prime.

Example \(\PageIndex{2}\)

Reduce \(10/40\) to lowest terms.

Solution

Note that \(\operatorname{GCD}(10,40)=10\). Divide numerator and denominator by \(10\).

\[\begin{aligned} \dfrac{10}{40} &=\dfrac{10 \div 10}{40 \div 10} \quad \color{Red} \text{Divide numerator and denominator by } \operatorname{GCD}(10,40)=10 \\ &=\dfrac{1}{4} \quad \color{Red} \text{Simplify numerator and denominator.}\\ \text{Thus, } 10/40 &= 1/4 \end{aligned} \nonumber\]

Alternate Solution

Use factor trees to express both numerator and denominator as a product of prime factors.

Figure \(\PageIndex{1}\)

Hence, \(10=2 \cdot 5\) and \(40=2 \cdot 2 \cdot 2 \cdot 5\). Now, to reduce \(10/40\) to lowest terms, replace the numerator and denominator with their prime factorizations, then cancel factors that are in common to both numerator and denominator.

\[\begin{aligned}
\dfrac{10}{40} &=\dfrac{2 \cdot 5}{2 \cdot 2 \cdot 2 \cdot 5} \quad \color{Red} \text{Prime factor numerator and denominator.} \\
&=\dfrac{{\color{Red}\not}2 \cdot {\color{Red}\not}5}{{\color{Red}\not}2 \cdot 2 \cdot 2 \cdot {\color{Red}\not}5} \quad \color{Red} \text{Cancel common factors.} \\
&=\dfrac{1}{4} \quad \color{Red} \text{Simplify numerator and denominator.}
\end{aligned}\]

When we cancel a \(2\) from both the numerator and denominator, we’re actually dividing both numerator and denominator by \(2\). A similar statement can be made about canceling the \(5\). Canceling both \(2\) and a \(5\) is equivalent to dividing both numerator and denominator by \(10\). This explains the \(1\) in the numerator when all factors cancel.

Exercise \(\PageIndex{2}\)

Reduce \(18/ 24\) to lowest terms. .

Answer

\(3/ 4\)

Example \(\PageIndex{2}\) demonstrates an important point.

When all factors cancel

When all of the factors cancel in either numerator or denominator, the resulting numerator or denominator is equal to one.

Multiplying Fractions

First, the definition.

Multiplication of Fractions

If \(a/b\) and \(c/d\) are two fractions, then their product is defined as follows:

\[\dfrac{a}{b} \cdot \dfrac{c}{d}=\dfrac{a c}{b d} \nonumber \]

Thus, to find the product of \(a/b\) and \(c/d\), simply multiply numerators and multiply denominators. For example:

\[\dfrac{1}{2} \cdot \dfrac{3}{4}=\dfrac{3}{8} \quad \text { and } \quad -\dfrac{2}{5} \cdot \dfrac{7}{3}= -\dfrac{14}{15} \quad \text { and } \quad -\dfrac{5}{8} \cdot \left(-\dfrac{1}{6} \right)=\dfrac{5}{48} \nonumber \]

Like integer multiplication, like signs yield a positive answer, unlike signs yield a negative answer. Of course, when necessary, remember to reduce your answer to lowest terms.

Example \(\PageIndex{3}\)

Simplify: \(-\dfrac{14}{20} \cdot \dfrac{10}{21}\).

Solution

Multiply numerators and denominators, then reduce to lowest terms.

\[\begin{aligned}
-\dfrac{14}{20} \cdot \dfrac{10}{21} &=-\dfrac{140}{420} \quad \color{Red} \text{Multiply numerators and denominators} \\
&=-\dfrac{2 \cdot 2 \cdot 5 \cdot 7}{2 \cdot 2 \cdot 3 \cdot 5 \cdot 7} \quad \color{Red} \text{Prime factor.} \\
&=-\dfrac{{\color{Red}\not}2 \cdot {\color{Red}\not}2 \cdot {\color{Red}\not}5 \cdot {\color{Red}\not}7}{{\color{Red}\not}2 \cdot {\color{Red}\not}2 \cdot 3 \cdot {\color{Red}\not}5 \cdot {\color{Red}\not}7} \quad \color{Red} \text{Cancel common factors.} \\
&=-\dfrac{1}{3} \quad \color{Red} \text{Simplify.}
\end{aligned} \nonumber \]

Note that when all the factors cancel from the numerator, you are left with a \(1\). Thus, \((-14/20)\cdot (10/21) = -1/3\).

Exercise \(\PageIndex{3}\)

Simplify: \(-\dfrac{8}{9} \cdot\left(-\dfrac{27}{20}\right)\).

Answer

\(6/5\)

Cancellation Rule

When multiplying fractions, cancel common factors according to the following rule: “Cancel a factor in a numerator for an identical factor in a denominator.”

The rule is “cancel something on the top for something on the bottom.” Thus, an alternate approach to multiplying fractions is to factor numerators and denominators in place, then cancel a factor in a numerator for an identical factor in a denominator.

Example \(\PageIndex{4}\)

Simplify: \(\dfrac{15}{8} \cdot\left(-\dfrac{14}{9}\right)\).

Solution

Factor numerators and denominators in place, then cancel common factors in the numerators for common factors in the denominators.

\[\begin{aligned}
\dfrac{15}{8} \cdot\left(-\dfrac{14}{9}\right) &=\dfrac{3 \cdot 5}{2 \cdot 2 \cdot 2} \cdot\left(-\dfrac{2 \cdot 7}{3 \cdot 3}\right) \quad \color{Red} \text{Factor numerators and denominators.} \\
&=\dfrac{{\color{Red}\not}3 \cdot 5}{{\color{Red}\not}2 \cdot 2 \cdot 2} \cdot\left(-\dfrac{{\color{Red}\not}2 \cdot 7}{{\color{Red}\not}3 \cdot 3}\right) \quad \color{Red} \text{Cancel a factor in a numerator for a common factor in a denominator.} \\
&=-\dfrac{35}{12} \quad \color{Red} \text{Multiply numerators and denominators.}
\end{aligned} \nonumber \]

Note that unlike signs yield a negative product. Thus, \((15/8)\cdot (-14/9) = -35/12\).

Exercise \(\PageIndex{4}\)

Simplify: \(-\dfrac{6}{45} \cdot\left(-\dfrac{35}{14}\right)\)

Answer

\(1/3\)

Dividing Fractions

Every nonzero rational number has a multiplicative inverse or reciprocal.

The Reciprocal

If \(a\) is any nonzero rational number, then \(1/a\) is called the multiplicative inverse or reciprocal of \(a\), and:

\[a \cdot \dfrac{1}{a}=1 \nonumber \]

Note that:

\[2 \cdot \dfrac{1}{2}=1 \quad \text { and } \quad \dfrac{3}{5} \cdot \dfrac{5}{3}=1 \quad \text { and } \quad -\dfrac{4}{7} \cdot\left(-\dfrac{7}{4}\right)=1 \nonumber \]

Thus, the reciprocal of \(2\) is \(1/2\), the reciprocal of \(3/5\) is \(5/3\), and the reciprocal of \(-4/7\) is \(-7/4\). Note that to find the reciprocal of a number, simply invert the number (flip it upside down). Now we can define the quotient of two fractions.

Division of Fractions

If \(a/b\) and \(c/d\) are two fractions, then their quotient is defined as follows:

\[\dfrac{a}{b} \div \dfrac{c}{d}=\dfrac{a}{b} \cdot \dfrac{d}{c} \nonumber \]

The above definition of division is summarized by the phrase “invert and multiply.”

Example \(\PageIndex{5}\)

Simplify: \(-\dfrac{35}{21} \div\left(-\dfrac{10}{12}\right)\).

Solution

Invert and multiply, then factor in place and cancel common factors in a numerator for common factors in a denominator.

\[\begin{aligned}
-\dfrac{35}{21} \div\left(-\dfrac{10}{12}\right) &=-\dfrac{35}{21} \cdot\left(-\dfrac{12}{10}\right) \quad \color{Red} \text{Invert and multiply.} \\
&=-\dfrac{5 \cdot 7}{3 \cdot 7} \cdot\left(-\dfrac{2 \cdot 2 \cdot 3}{2 \cdot 5}\right) \quad \color{Red} \text{Prime factor.} \\
&=-\dfrac{{\color{Red}\not}5 \cdot {\color{Red}\not}7}{{\color{Red}\not}3 \cdot {\color{Red}\not}7} \cdot\left(-\dfrac{{\color{Red}\not}2 \cdot 2 \cdot {\color{Red}\not}3}{{\color{Red}\not}2 \cdot {\color{Red}\not}5}\right) \quad \color{Red} \text{Cancel common factors.} \\
&=\dfrac{2}{1} \quad \color{Red} \text{Multiply numerators and denominators.} \\ &=2 \quad \color{Red} \text{Simplify.} \end{aligned} \nonumber \]

Note that when all the factors in a denominator cancel, a \(1\) remains. Thus, \((-35/21)÷(-10/12) = 2\). Note also that like signs yield a positive result.

Exercise \(\PageIndex{5}\)

Simplify: \(-\dfrac{4}{9} \div \dfrac{27}{81}\).

Answer

\(-4/3\)

Adding Fractions

First the definition.

Addition of Fractions

If two fractions have a denominator in common, add the numerators and place the result over the common denominator. In symbols:

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \nonumber \]

For example:

\[-\dfrac{3}{5}+\dfrac{7}{5}=\dfrac{4}{5} \quad \text { and } \quad-\dfrac{4}{3}+\left(-\dfrac{7}{3}\right)=-\dfrac{11}{3} \quad \text { and } \quad \dfrac{4}{7}+\left(-\dfrac{5}{7}\right)=-\dfrac{1}{7} \nonumber \]

If the fractions do not posses a common denominator, first create equivalent fractions with a least common denominator, then add according to the rule above.

Least Common Denominator

If the fractions \(a/b\) and \(c/d\) do not share a common denominator, the least common denominator for \(b\) and \(d\), written \(\mathrm{LCD}(b, d)\), is defined as the smallest number divisible by both \(b\) and \(d\).

Example \(\PageIndex{6}\)

Simplify: \(-\dfrac{3}{8}+\dfrac{5}{12}\).

Solution

The least common denominator in this case is the smallest number divisible by both \(8\) and \(12\). In this case, \(\mathrm{LCD}(8,12)=24\). We first need to make equivalent fractions with a common denominator of \(24\).

\[\begin{aligned} -\dfrac{3}{8}+\dfrac{5}{12} &=-\dfrac{3}{8} \cdot \dfrac{\color{Red}3}{\color{Red}3}+\dfrac{5}{12} \cdot \dfrac{\color{Red}2}{\color{Red}2} \quad \color{Red} \text{Make equivalent fraction with a common denominator of } 24 \\ &=-\dfrac{9}{24}+\dfrac{10}{24} \quad \color{Red} \text{Multiply numerators and denominators.}\\ &=\dfrac{1}{24} \quad \color{Red} \text{Add: } -9+10=1 \end{aligned} \nonumber\]

Note how we add the numerators in the last step, placing the result over the common denominator. Thus, \(-3/8+5/12 = 1/24\).

Exercise \(\PageIndex{6}\)

Simplify: \(-\dfrac{5}{6}+\dfrac{1}{9}\).

Answer

\(-13/18\)

Order of Operations

Rational numbers obey the same Rules Guiding Order of Operations as do the integers.

Rules Guiding Order of Operations

When evaluating expressions, proceed in the following order.

1. Evaluate expressions contained in grouping symbols first. If grouping symbols are nested, evaluate the expression in the innermost pair of grouping symbols first.
2. Evaluate all exponents that appear in the expression.
3. Perform all multiplications and divisions in the order that they appear in the expression, moving left to right.
4. Perform all additions and subtractions in the order that they appear in the expression, moving left to right.

Example \(\PageIndex{7}\)

Given \(x =2 /3\), \(y = -3/5\), and \(z = 10 /9\), evaluate \(xy + yz\).

Solution

Following Tips for Evaluating Algebraic Expressions, first replace all occurrences of variables in the expression \(xy + yz\) with open parentheses. Next, substitute the given values of variables (\(2/3\) for \(x\), \(-3/5\) for \(y\), and \(10 /9\) for \(z\)) in the open parentheses.

\[\begin{aligned} x y+y z &=( )(\;\;)+(\;\;)(\;\;) \quad \color{Red} \text{Replace variables with parentheses}\\ &=\left(\dfrac{2}{3}\right)\left(-\dfrac{3}{5}\right)+\left(-\dfrac{3}{5}\right)\left(\dfrac{10}{9}\right) \quad \color{Red} \text{Substitute: } 2/3 \text{ for } x,-3/5 \text{ for } y, \text{ and } 10/9 \text{ for } z \end{aligned} \nonumber \]

Use the Rules Guiding Order of Operations to simplify.

\[\begin{aligned}
&=-\dfrac{6}{15}+\left(-\dfrac{30}{45}\right) \quad \color{Red} \text{Multiply}\\
&=-\dfrac{2}{5}+\left(-\dfrac{2}{3}\right) \quad \color{Red} \text{Reduce} \\
&=-\dfrac{2}{5} \cdot \dfrac{3}{3}+\left(-\dfrac{2}{3} \cdot \dfrac{5}{5}\right) \quad \color{Red} \text{Make equivalent fractions with a }\\
&=-\dfrac{6}{15}+\left(-\dfrac{10}{15}\right) \quad \color{Red} \text{Least Common Denominator}\\
&=-\dfrac{16}{15} \quad \color{Red} \text{Add}
\end{aligned} \nonumber \]

Thus, if \(x=2 / 3, y=-3 / 5,\) and \(z=10 / 9,\) then \(x y+y z=-16 / 15\)

Exercise \(\PageIndex{7}\)

Given \(a=-1 / 2, b=2 / 3\) and \(c=-3 / 4\), evaluate the expression \(a+bc\) and simplify the result.

Answer

\(-1\)

Example \(\PageIndex{8}\)

Given \(x=-3/5\), evaluate \(-x^{3}\).

Solution

First, replace each occurrence of the variable \(x\) with open parentheses, then substitute \(-3/5\) for \(x\).

\[\begin{aligned}
-x^{3} &=-( )^{3} \quad \color{Red} \text{Replace x with open parentheses.}\\
&=-\left(-\dfrac{3}{5}\right)^{3} \quad \color{Red} \text{Substitute -3/5 for x}\\
&=-\left(-\dfrac{3}{5}\right)\left(-\dfrac{3}{5}\right)\left(-\dfrac{3}{5}\right) \quad \color{Red} \text{Write -3/5 as a factor three times}\\
&=-\left(-\dfrac{27}{125}\right) \quad \color{Red} \text{The product of three negative fractions is negative. Multiply numerators and denominators.}\\
&=\dfrac{27}{125} \quad \color{Red} \text{The opposite of -27/125 is 27/125}
\end{aligned} \nonumber \]

Hence, \(-x^{3}=27 / 125\), given \(x=-3/5\).

Exercise \(\PageIndex{8}\)

Simplify: \((-1 / 3)^{4}\).

Answer

\(1/81\)

Example \(\PageIndex{9}\)

Given \(a=-4/3\) and \(b=-3 / 2\), evaluate \(a^{2}+2 a b-3 b^{2}\).

Solution

Following Tips for Evaluating Algebraic Expressions, first replace all occurrences of variables in the expression \(a^{2}+2 a b-3 b^{2}\) with open parentheses.

Next, substitute the given values of variables (\(-4/3\) for \(a\) and \(-3/2\) for \(b\)) in the open parentheses.

\[\begin{aligned} a^{2}+2 a b-3 b^{2} &=(\;\; )^{2}+2(\;\; )( \;\;)-3(\; ) ^{2} \\ &=\left(-\dfrac{4}{3}\right)^{2}+2\left(-\dfrac{4}{3}\right)\left(-\dfrac{3}{2}\right)-3\left(-\dfrac{3}{2}\right)^{2} \end{aligned} \nonumber \]

Next, evaluate the exponents: \((-4 / 3)^{2}=16 / 9\) and \((-3 / 2)^{2}=9 / 4\)
\[=\dfrac{16}{9}+\dfrac{2}{1}\left(-\dfrac{4}{3}\right)\left(-\dfrac{3}{2}\right)-\dfrac{3}{1}\left(\dfrac{9}{4}\right) \nonumber \]

Next, perform the multiplications and reduce.

\[\begin{array}{l}{=\dfrac{16}{9}+\dfrac{24}{6}-\dfrac{27}{4}} \\ {=\dfrac{16}{9}+4-\dfrac{27}{4}}\end{array} \nonumber \]

Make equivalent fractions with a common denominator, then add.

\[\begin{array}{l}{=\dfrac{16}{9} \cdot {\color{Red} \dfrac{4}{4}}+4 \cdot {\color{Red} \dfrac{36}{36}}-\dfrac{27}{4} \cdot {\color{Red} \dfrac{9}{9}}} \\ {=\dfrac{64}{36}+\dfrac{144}{36}-\dfrac{243}{36}} \\ {=-\dfrac{35}{36}}\end{array} \nonumber \]

Thus, if \(a=-4 / 3\) and \(b=-3 / 2\), then \(a^{2}+2 a b-3 b^{2}=-35 / 36\)

Exercise \(\PageIndex{9}\)

Given \(x=-3 / 4\) and \(y=-4 / 5\) ,evaluate \(x^{2}-y^{2}\).

Answer

\(-31/400\)

Fractions on the Graphing Calculator

We must always remember that the graphing calculator is an “approximating machine.” In a small number of situations, it is capable of giving an exact answer, but for most calculations, the best we can hope for is an approximate answer.

However, the calculator gives accurate results for operations involving fractions, as long as we don’t use fractions with denominators that are too large for the calculator to respond with an exact answer.

Example \(\PageIndex{10}\)

Use the graphing calculator to simplify each of the followingSimplify using the graphing calculator:

1. \(\dfrac{2}{3}+\dfrac{1}{2}\)
2. \(\dfrac{2}{3} \cdot \dfrac{5}{7}\)
3. \(\dfrac{3}{5} \div \dfrac{1}{3}\)

Solution

We enter each expression in turn.

1. The Rules Guiding Order of Operations tell us that we must perform divisions before additions. Thus, the expression \(2/3+1/2\) is equivalent to:
   \[\begin{aligned} 2 / 3+1 / 2 &=\dfrac{2}{3}+\dfrac{1}{2} \quad \color{Red} \text{Divide first.}\\ &=\dfrac{4}{6}+\dfrac{3}{6} \quad \color{Red} \text{Equivalent fractions with LCD.}\\ &=\dfrac{7}{6} \quad \color{Red} \text{Add.} \end{aligned} \nonumber \]Enter the expression \(2/3+1/2\) on your calculator, then press the ENTER key. The result is shown in the first image in Figure \(\PageIndex{2}\). Next, press the MATH button, then select 1:Frac (see the second image in Figure \(\PageIndex{2}\)) and press the ENTER key again. Note that the result shown in the third image in Figure \(\PageIndex{2}\) matches the correct answer of \(7/6\) found above.

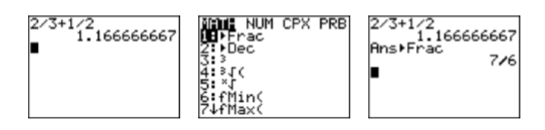
Figure \(\PageIndex{2}\): Calculating \(2/3+1/2\).

2. The Rules Guiding Order of Operations tell us that there is no preference for division over multiplication, or vice-versa. We must perform divisions and multiplications as they occur, moving from left to right. Hence: \[\begin{aligned}
   2 / 3 \times 5 / 7 &=\dfrac{2}{3} \times 5 / 7 \quad \color{Red} \text{Divide: } 2/3=\dfrac{2}{3}\\
   &=\dfrac{10}{3} / 7 \quad \color{Red} \text{Multiply: } \dfrac{2}{3}\times 5=\dfrac{10}{3}\\
   &=\dfrac{10}{3} \times \dfrac{1}{7} \quad \color{Red} \text{Invert and multiply.}\\
   &=\dfrac{10}{21} \quad \color{Red} \text{Multiply: } \dfrac{10}{3}\times \dfrac{1}{7}=\dfrac{10}{21}
   \end{aligned} \nonumber \] This is precisely the same result we get when we perform the following calculation. \[\dfrac{2}{3} \times \dfrac{5}{7}=\dfrac{10}{21} \quad \color{Red} \text{Multiply numerators and denominators.} \nonumber \] Hence: \[2 / 3 \times 5 / 7 \quad \text { is equivalent to } \quad \dfrac{2}{3} \times \dfrac{5}{7} \nonumber \]Enter the expression \(2/3×5/7\) on your calculator, then press the ENTER key. The result is shown in the first image in Figure \(\PageIndex{3}\). Next, press the MATH button, then select 1:Frac (see the second image in Figure \(\PageIndex{3}\)) and press the ENTER key again. Note that the result shown in the third image in Figure \(\PageIndex{3}\) matches the correct answer of \(10/21\) found above.

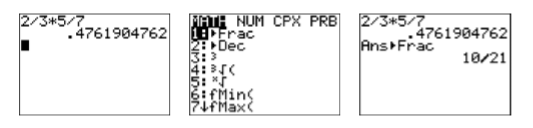
Figure \(\PageIndex{3}\): Calculating \(2/3×1/2\).

3. This example demonstrates that we need a constant reminder of the Rules Guiding Order of Operations. We know we need to invert and multiply in this situation. \[\begin{aligned} \dfrac{3}{5} \div \dfrac{1}{3}&= \dfrac{3}{5} \times \dfrac{3}{1} \quad \color{Red} \text { Invert and multiply. } \\ &=\dfrac{9}{5} \quad \color{Red} \text { Multiply numerators and denominators. } \end{aligned} \nonumber \]
   So, the correct answer is 9/5. Enter the expression \(3/5/1/3\) on your calculator, then press the ENTER key. Select 1:Frac from the MATH menu and press the ENTER key again. Note that the result in the first image in Figure \(\PageIndex{4}\) does not match the correct answer of \(9/5\) found above. What have we done wrong? If we follow the Rules Guiding Order of Operations exactly, then: \[\begin{aligned}
   3 / 5 / 1 / 3 & =\dfrac{3}{5} / 1 / 3 \quad \color{Red} \text {Divide: } 3/5=\dfrac{3}{5} \\
   & =\dfrac{3}{5} / 3 \quad \color{Red} \text { Divide: } \dfrac{3}{5} / 1=\dfrac{3}{5} \\
   & =\dfrac{3}{5} \times \dfrac{1}{3} \quad \color{Red} \text {Invert and multiply.} \\
   & =\dfrac{1}{5} \quad \color{Red} \text {Multiply: } \dfrac{3}{5} \times \dfrac{1}{3}=\dfrac{1}{5}
   \end{aligned} \nonumber\] This explains the answer found in the first image in Figure \(\PageIndex{4}\). However, it also show that: \[ 3 / 5 / 1 / 3 \quad \text { is not equivalent to } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \] We can cure the problem by using grouping symbols. \[\begin{aligned} (3 / 5) /(1 / 3) &=\dfrac{3}{5} / \dfrac{1}{3} \quad \color{Red} \text { Parentheses first. } \\ &=\dfrac{3}{5} \div \dfrac{1}{3} \quad \color{Red} \text { is equivalent to } \div \end{aligned} \nonumber \] Hence: \[(3 / 5) /(1 / 3) \quad \text { is equivalent to } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \]Enter the expression \((3/5)/(1/3)\) on your calculator, then press the ENTER key. Select 1:Frac from the MATH menu and press the ENTER key again. Note that the result in the second image in Figure \(\PageIndex{4}\) matches the correct answer of \(9/5\).

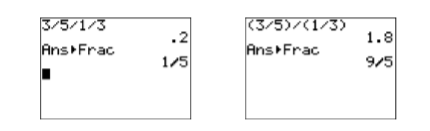
Figure \(\PageIndex{4}\): Calculating \((3/5)/(1/3)\).

Exercise \(\PageIndex{10}\)

Simplify using the graphing calculator: \(-\dfrac{4}{5}+\dfrac{8}{3}\).

Answer

\(28/15\)

Contributors

• David Arnold (Retired Professor (Mathematics) at College of the Redwoods)