2.3: Clearing Fractions and Decimals

Last updated
Save as PDF

Page ID: 19858

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In this section we introduce techniques that clear fractions and decimals from equations, making the resulting equation a lot easier to solve. When clearing fractions from an equation, you will need to simplify products like the ones posed in the following examples.

Example $\PageIndex{1}$

Simplify: $12\left(\dfrac{2}{3} x\right)$.

Solution

When we multiply three numbers, such as $12$, $2/3$, and $x$, the associative property of multiplication tells us that it does not matter which two numbers we multiply ﬁrst. We use the associative property to regroup, then multiply numerators and denominators and simplify the result.

\[\begin{aligned} 12\left(\dfrac{2}{3} x\right) &=\left(12 \cdot \dfrac{2}{3}\right) x \quad \color{Red} \text{Associative property of multiplication.}\\ &=\dfrac{24}{3} x \quad \color{Red} \text { Multiply: } 12 \cdot 2=24 \\ &=8 x \quad \color{Red} \text { Divide: } 24 / 3=8 \end{aligned} \nonumber \]

Exercise $\PageIndex{1}$

Simplify: $15\left(\dfrac{3}{5} x\right)$.

Answer: $9x$

Example $\PageIndex{1}$ shows all of the steps involved in arriving at the answer. However, the goal in this section is to perform this calculation mentally. So we just “Multiply $12$ and $2$ to get $24$, then divide $24$ by $3$ to get $8$.” This approach allows us to write down the answer without doing any work.

\[12\left(\dfrac{2}{3} x\right)=8 x \nonumber \]

You should practice this mental calculation until you can write down the answer without writing down any steps.

Example $\PageIndex{2}$

Simplify: $18 \left(\dfrac{2}{9} x\right)$.

Solution

This time we perform the calculations mentally. Multiply $18$ and $2$ to get $36$, then divide $36$ by $9$ to get $4$.

\[18\left(\dfrac{2}{9} x\right)=4 x \nonumber \]

Exercise $\PageIndex{2}$

Simplify: $14 \left(\dfrac{3}{7} x\right)$.

Answer: $6x$

When the numbers get larger, the mental calculations become harder. For example, consider \[72\left(\dfrac{8}{9} x\right) \nonumber \]

In this case, the work “multiply $72$ and $8$ to get $576$, then divide $576$ by $9$ to get $64$” is a bit diﬃcult to carry in your head. However, this is when the calculator comes to the rescue.

Example $\PageIndex{3}$

Use your calculator to help simplify $72 \left(\dfrac{8}{9} x\right)$.

Solution

Use your calculator to multiply $72$ and $8$, then divide by $9$. Enter 72*8/9 and press the ENTER key.

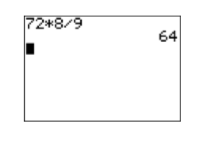
$fig 2.3.1a.png$

Thus, $72\left(\dfrac{8}{9} x\right)=64 x$.

Exercise $\PageIndex{3}$

Use your calculator to simplify: $81 \left(\frac{5}{9} x\right)$.

Answer: $45x$

Canceling is more eﬃcient

In Examples $\PageIndex{1}$, $\PageIndex{2}$, and $\PageIndex{3}$, we multiplied numerators, then divided by the sole denominator. We also saw that it is a bit diﬃcult to carry the work in our head as the numbers grow larger. In Chapter 1, Section 3, we saw that canceling reduces the size of the numbers and simpliﬁes the work.

Example $\PageIndex{4}$

Simplify: $72 \left(\dfrac{8}{9} x\right)$.

Solution

In Example $\PageIndex{3}$, we used our calculator to multiply $72$ and $8$ to get $576$, then divided $576$ by $9$ to get $64$. In this solution, we divide $9$ into $72$ to get $8$, then multiply $8$ by $8$ to get $64$. We get the same answer, but because the intermediate numbers are much smaller, the calculations are much easier to do mentally.

\[\begin{aligned} 72\left(\dfrac{8}{9} x\right) &=\left(72 \cdot \dfrac{8}{9}\right) x \quad \color{Red} \text{Associative property of multiplication}\\ &=(8 \cdot 8) x \quad \color{Red} \text { Divide: } 72 / 9=8 \\ &=64 x \quad \color{Red} \text { Multiply: } 8 \cdot 8=64 \end{aligned} \nonumber \]

Exercise $\PageIndex{4}$

Simplify: $64 \left(\dfrac{5}{8} x\right)$.

Answer: $40x$

Example $\PageIndex{4}$ shows all of the steps involved in arriving at the answer. Again, the goal in this section is to perform this calculation mentally, so we just “Divide $9$ into $72$ to get $8$, then multiply $8$ by $8$ to get $644$.”

\[72\left(\frac{8}{9} x\right)=64 x \nonumber \]

Not only does this approach allow us to write down the answer without doing any work, the numerical calculations involve smaller numbers. You should practice this mental calculation until you can write down the answer without writing down any steps.

Example $\PageIndex{5}$

Simplify: $27\left(\dfrac{5}{9} x\right)$.

Solution

Divide $9$ into $27$ to get $3$, then multiply $3$ by $5$ to get $15$. \[27\left(\dfrac{5}{9} x\right)=15 x \nonumber \]

Exercise $\PageIndex{5}$

Simplify: $18\left(\dfrac{3}{2} x\right)$.

Answer: $27x$

Note

The technique shown in Examples $\PageIndex{4}$ and $\PageIndex{5}$ is the technique we’ll use in the remainder of this section. Dividing (canceling) ﬁrst is far more eﬃcient, the smaller numbers allowing us to perform the calculation mentally.

Clearing Fractions from an Equation

Now that we’ve done the required fraction work, we can now concentrate on clearing fractions from an equation. Once the fractions are removed from the equation, the resulting equivalent equation is far easier to solve than the original.

Clearing fractions from an equation

To clear fractions from an equation, multiply both sides of the equation by the least common denominator.

Example $\PageIndex{6}$

Add text here.

Solution

Add text here.

Exercise $\PageIndex{6}$

Add exercises text here.

Answer: Add texts here. Do not delete this text first.

Contributors

David Arnold (Retired Professor (Mathematics) at College of the Redwoods)