7.3E: Exercises
- Page ID
- 30261
Practice Makes Perfect
Recognize a Preliminary Strategy to Factor Polynomials Completely
In the following exercises, identify the best method to use to factor each polynomial.
- \(10q^2+50\)
- \(a^2−5a−14\)
- \(uv+2u+3v+6\)
- Answer
-
- factor the GCF, binomial
- Undo FOIL
- factor by grouping
- \(n^2+10n+24\)
- \(8u^2+16\)
- \(pq+5p+2q+10\)
- \(x^2+4x−21\)
- \(ab+10b+4a+40\)
- \(6c^2+24\)
- Answer
-
- undo FOIL
- factor by grouping
- factor the GCF, binomial
- \(20x^2+100\)
- \(uv+6u+4v+24\)
- \(y^2−8y+15\)
In the following exercises, factor completely.
\(5x^2+35x+30\)
- Answer
-
\(5(x+1)(x+6)\)
\(12s^2+24s+12\)
\(2z^2−2z−24\)
- Answer
-
\(2(z−4)(z+3)\)
\(3u^2−12u−36\)
\(7v^2−63v+56\)
- Answer
-
\(7(v−1)(v−8)\)
\(5w^2−30w+45\)
\(p^3−8p^2−20p\)
- Answer
-
\(p(p−10)(p+2)\)
\(q^3−5q^2−24q\)
\(3m^3−21m^2+30m\)
- Answer
-
\(3m(m−5)(m−2)\)
\(11n^3−55n^2+44n\)
\(5x^4+10x^3−75x^2\)
- Answer
-
\(5x^{2}(x−3)(x+5)\)
\(6y^4+12y^3−48y^2\)
Factor Trinomials Using Trial and Error
In the following exercises, factor.
\(2t^2+7t+5\)
- Answer
-
\((2t+5)(t+1)\)
\(5y^2+16y+11\)
\(11x^2+34x+3\)
- Answer
-
\((11x+1)(x+3)\)
\(7b^2+50b+7\)
\(4w^2−5w+1\)
- Answer
-
\((4w−1)(w−1)\)
\(5x^2−17x+6\)
\(6p^2−19p+10\)
- Answer
-
\((3p−2)(2p−5)\)
\(21m^2−29m+10\)
\(4q^2−7q−2\)
- Answer
-
\((4q+1)(q−2)\)
\(10y^2−53y−11\)
\(4p^2+17p−15\)
- Answer
-
\((4p−3)(p+5)\)
\(6u^2+5u−14\)
\(16x^2−32x+16\)
- Answer
-
\(16(x−1)(x−1)\)
\(81a^2+153a−18\)
\(30q^3+140q^2+80q\)
- Answer
-
\(10q(3q+2)(q+4)\)
\(5y^3+30y^2−35y\)
In the following exercises, factor.
\(5n^2+21n+4\)
- Answer
-
\((5n+1)(n+4)\)
\(8w^2+25w+3\)
\(9z^2+15z+4\)
- Answer
-
\((3z+1)(3z+4)\)
\(3m^2+26m+48\)
\(4k^2−16k+15\)
- Answer
-
\((2k−3)(2k−5)\)
\(4q^2−9q+5\)
\(5s^2−9s+4\)
- Answer
-
\((5s−4)(s−1)\)
\(4r^2−20r+25\)
\(6y^2+y−15\)
- Answer
-
\((3y+5)(2y−3)\)
\(6p^2+p−22\)
\(2n^2−27n−45\)
- Answer
-
\((2n+3)(n−15)\)
\(12z^2−41z−11\)
\(3x^2+5x+4\)
- Answer
-
prime
\(4y^2+15y+6\)
\(60y^2+290y−50\)
- Answer
-
\(10(6y−1)(y+5)\)
\(6u^2−46u−16\)
\(48z^3−102z^2−45z\)
- Answer
-
\(3z(8z+3)(2z−5)\)
\(90n^3+42n^2−216n\)
\(16s^2+40s+24\)
- Answer
-
\(8(2s+3)(s+1)\)
\(24p^2+160p+96\)
\(48y^2+12y−36\)
- Answer
-
\(12(4y−3)(y+1)\)
\(30x^2+105x−60\)
In the following exercises, factor.
\(12y^2−29y+14\)
- Answer
-
\((4y−7)(3y−2)\)
\(12x^2+36y−24z\)
\(a^2−a−20\)
- Answer
-
\((a−5)(a+4)\)
\(m^2−m−12\)
\(6n^2+5n−4\)
- Answer
-
\((2n−1)(3n+4)\)
\(12y^2−37y+21\)
\(2p^2+4p+3\)
- Answer
-
prime
\(3q^2+6q+2\)
\(13z^2+39z−26\)
- Answer
-
\(13(z^2+3z−2)\)
\(5r^2+25r+30\)
\(x^2+3x−28\)
- Answer
-
\((x+7)(x−4)\)
\(6u^2+7u−5\)
\(3p^2+21p\)
- Answer
-
\(3p(p+7)\)
\(7x^2−21x\)
\(6r^2+30r+36\)
- Answer
-
\(6(r+2)(r+3)\)
\(18m^2+15m+3\)
\(24n^2+20n+4\)
- Answer
-
\(4(2n+1)(3n+1)\)
\(4a^2+5a+2\)
\(x^2+2x−24\)
- Answer
-
\((x+6)(x−4)\)
\(2b^2−7b+4\)
Everyday Math
Height of a toy rocket The height of a toy rocket launched with an initial speed of \(80\) feet per second from the balcony of an apartment building is related to the number of seconds, \(t\), since it is launched by the trinomial \(−16t^2+80t+96\). Factor this trinomial.
- Answer
-
\(−16(t−6)(t+1)\)
Height of a beach ball The height of a beach ball tossed up with an initial speed of \(12\) feet per second from a height of \(4\) feet is related to the number of seconds, \(t\), since it is tossed by the trinomial \(−16t^2+12t+4\). Factor this trinomial.
Writing Exercises
List, in order, all the steps you take when using the “\(ac\)” method to factor a trinomial of the form \(ax^2+bx+c\).
- Answer
-
Answers may vary.
How is the “\(ac\)” method similar to the “undo FOIL” method? How is it different?
What are the questions, in order, that you ask yourself as you start to factor a polynomial? What do you need to do as a result of the answer to each question?
- Answer
-
Answers may vary.
On your paper draw the chart that summarizes the factoring strategy. Try to do it without looking at the book. When you are done, look back at the book to finish it or verify it.
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
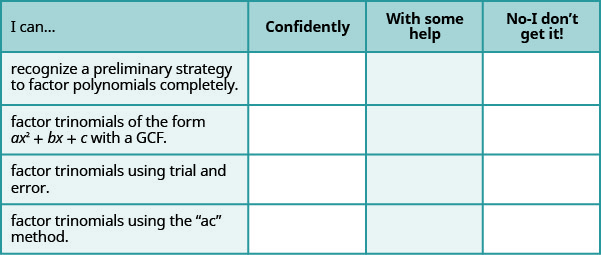
b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?


