4.7: Solve Systems of Equations Using Determinants
- Page ID
- 5143
By the end of this section, you will be able to:
- Evaluate the determinant of a 2×2 matrix
- Evaluate the determinant of a 3×3 matrix
- Use Cramer’s Rule to solve systems of equations
- Solve applications using determinants
Before you get started, take this readiness quiz.
In this section we will learn of another method to solve systems of linear equations called Cramer’s rule. Before we can begin to use the rule, we need to learn some new definitions and notation.
Evaluate the Determinant of a \(2×2\) Matrix
If a matrix has the same number of rows and columns, we call it a square matrix. Each square matrix has a real number associated with it called its determinant. To find the determinant of the square matrix \(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), we first write it as \(\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| \). To get the real number value of the determinate we subtract the products of the diagonals, as shown.
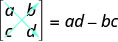
The determinant of any square matrix \(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), where a, b, c, and d are real numbers, is
\[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]
Evaluate the determinate of ⓐ \(\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] \) ⓑ \(\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] \).
- Answer
-
ⓐ
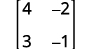
Write the determinant. 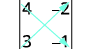
Subtract the products of the diagonals. 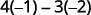
Simplify. 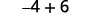
Simplify. 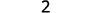
ⓑ
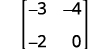
Write the determinant. 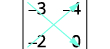
Subtract the products of the diagonals. 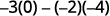
Simplify. 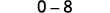
Simplify. 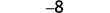
Evaluate the determinate of ⓐ \(\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] \) ⓑ \(\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] \).
- Answer
-
ⓐ \(−14\); ⓑ \(−28\)
Evaluate the determinate of ⓐ \(\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] \) ⓑ \(\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] \).
- Answer
-
ⓐ 2 ⓑ \(−15\)
Evaluate the Determinant of a \(3×3\) Matrix
To evaluate the determinant of a \(3×3\) matrix, we have to be able to evaluate the minor of an entry in the determinant. The minor of an entry is the \(2×2\) determinant found by eliminating the row and column in the \(3×3\) determinant that contains the entry.
The minor of an entry in a \(3×3\) determinant is the \(2×2\) determinant found by eliminating the row and column in the \(3×3\) determinant that contains the entry.
To find the minor of entry \(a_1\), we eliminate the row and column which contain it. So we eliminate the first row and first column. Then we write the \(2×2\) determinant that remains.

To find the minor of entry \(b_2\), we eliminate the row and column that contain it. So we eliminate the \(2^{nd}\) row and \(2^{nd}\) column. Then we write the \(2×2\) determinant that remains.

For the determinant \(\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|\), find and then evaluate the minor of ⓐ \(a_1\) ⓑ \(b_3\) ⓒ \(c_2\).
- Answer
-
ⓐ
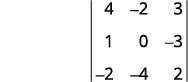
Eliminate the row and column that contains \(a_1\). 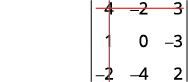
Write the \(2×2\) determinant that remains. 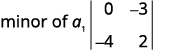
Evaluate. 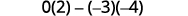
Simplify. 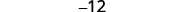
ⓑ
Eliminate the row and column that contains \(b_3\). 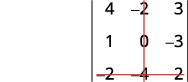
Write the \(2×2\) determinant that remains. 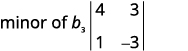
Evaluate. 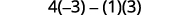
Simplify. 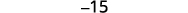
ⓒ
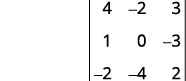
Eliminate the row and column that contains \(c_2\). 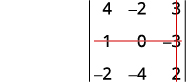
Write the \(2×2\) determinant that remains. 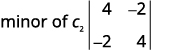
Evaluate. 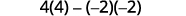
Simplify. 
For the determinant \(\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|\), find and then evaluate the minor of ⓐ \(a_1\) ⓑ \(b_2\) ⓒ \(c_3\).
- Answer
-
ⓐ 3 ⓑ 11 ⓒ 2
For the determinant \(\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|\), find and then evaluate the minor of ⓐ \(a_2\) ⓑ \(b_3\) ⓒ \(c_2\).
- Answer
-
ⓐ \(−3\) ⓑ 2 ⓒ 3
We are now ready to evaluate a \(3×3\) determinant. To do this we expand by minors, which allows us to evaluate the \(3×3\)determinant using \(2×2\) determinants—which we already know how to evaluate!
To evaluate a \(3×3\) determinant by expanding by minors along the first row, we use the following pattern:
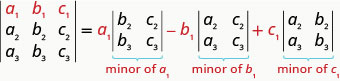
Remember, to find the minor of an entry we eliminate the row and column that contains the entry.
To evaluate a \(3×3\) determinant by expanding by minors along the first row, the following pattern:
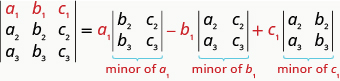
Evaluate the determinant \(\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|\) by expanding by minors along the first row.
- Answer
-

Expand by minors along the first row 
Evaluate each determinant. 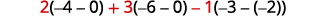
Simplify. 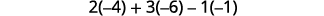
Simplify. 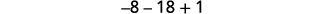
Simplify. 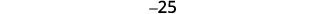
Evaluate the determinant \(\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|\), by expanding by minors along the first row.
- Answer
-
37
Evaluate the determinant \(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\), by expanding by minors along the first row.
- Answer
-
7
To evaluate a \(3×3\) determinant we can expand by minors using any row or column. Choosing a row or column other than the first row sometimes makes the work easier.
When we expand by any row or column, we must be careful about the sign of the terms in the expansion. To determine the sign of the terms, we use the following sign pattern chart.
\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
When expanding by minors using a row or column, the sign of the terms in the expansion follow the following pattern.\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Notice that the sign pattern in the first row matches the signs between the terms in the expansion by the first row.
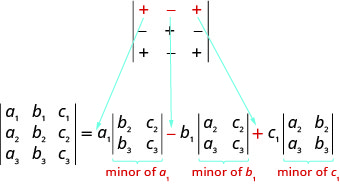
Since we can expand by any row or column, how do we decide which row or column to use? Usually we try to pick a row or column that will make our calculation easier. If the determinant contains a 0, using the row or column that contains the 0 will make the calculations easier.
Evaluate the determinant \(\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|\) by expanding by minors.
- Answer
-
To expand by minors, we look for a row or column that will make our calculations easier. Since 0 is in the second row and second column, expanding by either of those is a good choice. Since the second row has fewer negatives than the second column, we will expand by the second row.

Expand using the second row. Be careful of the signs. 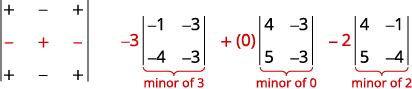
Evaluate each determinant. 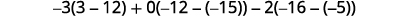
Simplify. 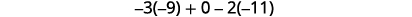
Simplify. 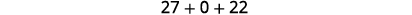
Add. 
Evaluate the determinant \(\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|\) by expanding by minors.
- Answer
-
\(−11\)
Evaluate the determinant \(\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|\) by expanding by minors.
- Answer
-
8
Use Cramer’s Rule to Solve Systems of Equations
Cramer’s Rule is a method of solving systems of equations using determinants. It can be derived by solving the general form of the systems of equations by elimination. Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables.
Let’s start with the systems of two equations with two variables.
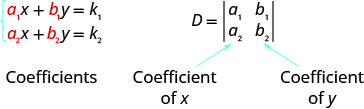
For the system of equations \(\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.\), the solution \((x,y)\) can be determined by

Notice that to form the determinant D, we use take the coefficients of the variables.
Notice that to form the determinant \(D_x\) and \(D_y\), we substitute the constants for the coefficients of the variable we are finding.
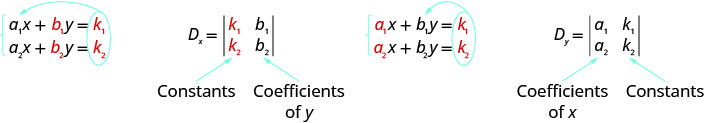
Solve using Cramer’s Rule: \(\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.\)
- Answer
-






Solve using Cramer’s rule: \(\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.\)
- Answer
-
\((−\frac{15}{7},\frac{24}{7})\)
Solve using Cramer’s rule: \(\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.\)
- Answer
-
\((−2,0)\)
- Evaluate the determinant D, using the coefficients of the variables.
- Evaluate the determinant \(D_x\). Use the constants in place of the x coefficients.
- Evaluate the determinant \(D_y\). Use the constants in place of the y coefficients.
- Find x and y. \(x=\frac{D_x}{D}\), \(y=\frac{D_y}{D}\)
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
To solve a system of three equations with three variables with Cramer’s Rule, we basically do what we did for a system of two equations. However, we now have to solve for three variables to get the solution. The determinants are also going to be \(3×3\) which will make our work more interesting!
For the system of equations \(\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.\), the solution \((x,y,z)\) can be determined by

Solve the system of equations using Cramer’s Rule: \(\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)
- Answer
-
Evaluate the determinant D. 
Expand by minors using column 1. 
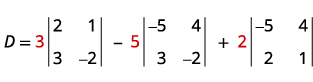
Evaluate the determinants. 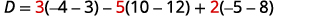
Simplify. 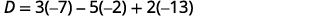
Simplify. 
Simplify. 
Evaluate the determinant \(D_x\). Use the
constants to replace the coefficients of x.
Expand by minors using column 1. 
Evaluate the determinants. 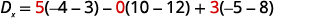
Simplify. 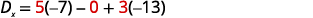
Simplify. 
Evaluate the determinant Dy.Dy. Use the
constants to replace the coefficients of y.

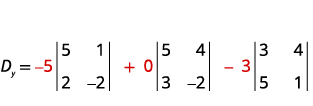
Evaluate the determinants. 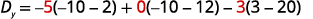
Simplify. 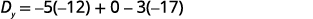
Simplify. 
Simplify. 
Evaluate the determinant Dz.Dz. Use the
constants to replace the coefficients of z.

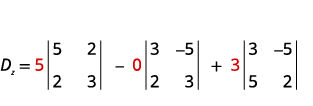
Evaluate the determinants. 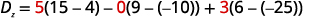
Simplify. 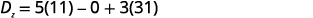
Simplify. 
Simplify. 
Find x, y, and z. 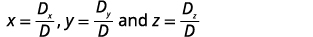
Substitute in the values. 
Simplify. 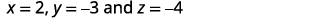
Write the solution as an ordered triple. 
Check that the ordered triple is a solution
to all three original equations.We leave the check to you. The solution is \((2,−3,−4)\).
Solve the system of equations using Cramer’s Rule: \(\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.\)
- Answer
-
\((−9,3,−1)\)
Solve the system of equations using Cramer’s Rule: \(\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.\)
- Answer
-
\((−6,3,−2)\)
Cramer’s rule does not work when the value of the D determinant is 0, as this would mean we would be dividing by 0. But when \(D=0\), the system is either inconsistent or dependent.
When the value of \(D=0\) and \(D_x,\space D_y\) and D are all zero, the system is consistent and dependent and there are infinitely many solutions.
When the value of \(D=0\) and \(D_x,\space D_y\) and \(D_z\) are not all zero, the system is inconsistent and there is no solution.
For any system of equations, where the value of the determinant \(D=0\),
\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
In the next example, we will use the values of the determinants to find the solution of the system.
Solve the system of equations using Cramer’s rule : \(\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.\)
- Answer
-
\(\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} \)
We cannot use Cramer’s Rule to solve this system. But by looking at the value of the determinants \(D_x\) and \(D_y\), we can determine whether the system is dependent or inconsistent.
\(\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} \)
Since all the determinants are not zero, the system is inconsistent. There is no solution.
Solve the system of equations using Cramer’s rule: \(\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.\)
- Answer
-
no solution
Solve the system of equations using Cramer’s rule: \(\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.\)
- Answer
-
infinite solutions
Solve Applications using Determinants
An interesting application of determinants allows us to test if points are collinear. Three points \((x_1,y_1)\), \((x_2,y_2)\) and \((x_3,y_3)\) are collinear if and only if the determinant below is zero.
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Three points \((x_1,y_1)\), \((x_2,y_2)\) and \((x_3,y_3)\) are collinear if and only if
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
We will use this property in the next example.
Determine whether the points \((5,−5)\), \((4,−3)\), and \((3,−1)\) are collinear.
- Answer
-
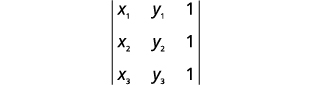
Substitute the values into the determinant.
\((5,−5)\), \((4,−3)\), and \((3,−1)\)
Evaluate the determinant by expanding
by minors using column 3.
Evaluate the determinants. 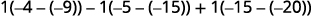
Simplify. 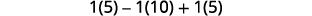
Simplify. 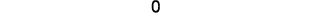
The value of the determinate is 0, so the
points are collinear.
Determine whether the points \((3,−2)\), \((5,−3)\), and \((1,−1)\) are collinear.
- Answer
-
yes
Determine whether the points \((−4,−1)\), \((−6,2)\), and \((−2,−4)\) are collinear.
- Answer
-
yes
Access these online resources for additional instruction and practice with solving systems of linear inequalities by graphing.
- Solving Systems of Linear Inequalities by Graphing
- Systems of Linear Inequalities
Key Concepts
- Determinant: The determinant of any square matrix \(\left[\begin{matrix}a&b\\c&d\end{matrix}\right]\), where a, b, c, and d are real numbers, is
\[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]
- Expanding by Minors along the First Row to Evaluate a 3 × 3 Determinant: To evaluate a \(3×3\) determinant by expanding by minors along the first row, the following pattern:
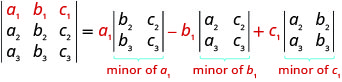
- Sign Pattern: When expanding by minors using a row or column, the sign of the terms in the expansion follow the following pattern.
\[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]
- Cramer’s Rule: For the system of equations \(\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.\), the solution \((x,y)\) can be determined by

Notice that to form the determinant D, we use take the coefficients of the variables. - How to solve a system of two equations using Cramer’s rule.
- Evaluate the determinant D, using the coefficients of the variables.
- Evaluate the determinant \(D_x\). Use the constants in place of the x coefficients.
- Evaluate the determinant \(D_y\). Use the constants in place of the y coefficients.
- Find x and y. \(x=\frac{D_x}{D}\), \(y=\frac{D_y}{D}\).
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
- Dependent and Inconsistent Systems of Equations: For any system of equations, where the value of the determinant \(D=0\),\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
- Test for Collinear Points: Three points \((x_1,y_1)\), \((x_2,y_2)\), and \((x_3,y_3)\) are collinear if and only if
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Glossary
- determinant
- Each square matrix has a real number associated with it called its determinant.
- minor of an entry in a 3×33×3 determinant
- The minor of an entry in a 3×33×3 determinant is the 2×22×2 determinant found by eliminating the row and column in the 3×33×3determinant that contains the entry.
- square matrix
- A square matrix is a matrix with the same number of rows and columns.


