2.8: Summary of Key Concepts

Last updated
Save as PDF

Page ID: 49352

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Summary of Key Concepts

Variables and Constants
A variable is a letter or symbol that represents any member of a collection of two or more numbers. A constant is a letter or symbol that represents a specific number.

Binary Operation
A binary operation is a process that assigns two numbers to a single number. +,−,×,÷ are binary operations.

Grouping Symbols

Grouping symbols are used to indicate that a particular collection of numbers and meaningful operations is to be considered as a single number (5÷0 is not meaningful). Grouping symbols can also direct us in operations when more than two operations are to be performed. Common algebraic grouping symbols are

Parentheses: ( )

Brackets: [ ]

Braces: { }

Bar: __

Order of Operations
When two or more operations are to be performed on a collection of numbers, the correct value can be
obtained only by using the correct order of operations.

The Real Number Line
The real number line allows us to visually display some of the numbers in which we are interested.

$Screen Shot 2021-02-04 at 4.04.32 PM.png$

Coordinate and Graph
The number associated with a point on the number line is called the coordinate of the point. The point associated with a number is called the graph of the number.

Real Number
A real number is any number that is the coordinate of a point on the real number line.

Types of Real Numbers

The collection of real numbers has many subcollections. The ones of most interest to us are

The Natural Numbers: ${1,2,3,…}$
The Whole Numbers: ${0,1,2,3,…}$
The Integers: ${…,-3,-2,-1,0,1,2,3,…}$
The Rational Numbers: { all numbers that can be expressed as the quotient of two integers }
The Irrational Numbers: { all numbers that have nonending and nonrepeating decimal representations }

Properties of Real Numbers

Closure: If $a$ and $b$ are real numbers, then $a+b$ and $a\cdot b$ are unique real numbers.
Commutative: $a + b = b + a$ and $a \cdot b = b \cdot a$.
Associative: $a + (b + c) = (a + b) + c$ and $a \cdot (b \cdot c) = (a \cdot b) \cdot c$
Distributive: $a(b + c) = a \cdot b. + a \cdot c$
Additive Identity: $0$ is the additive identity. $a + 0 = a$ and $0 + a = a$
Multiplicative Identity: $1$ is the multiplicative identity. $a \cdot 1 = a$ and $1 \cdot a = a$
Additive Inverse: For each real number $a$ there is exactly one number $-a$ such that $a + (-a) = 0$ and $(-a) + a = 0$.
Multiplicative Inverse: For each nonzero real number there is exactly one nonzero real number
$\dfrac{1}{a}$ such that $a \cdot \dfrac {1}{a} = 1$ and $\dfrac{1}{a} \cdot a = 1$.

Exponents
Exponents record the number of identical factors that appear in a multiplication.

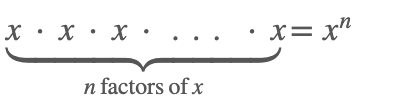
$Screen Shot 2021-02-04 at 4.11.58 PM.png$

Rules of Exponents
If $x$ is a real number and $n$ and $m$ are natural numbers, then

$x^n \cdot x^m = x^{n + m}$
$\dfrac{x^n}{x^m} = x^{n-m}, x \not = 0$
$x^0 = 1, x \not = 0$
$(x^n)^m = x^{n \cdot m}$
$(\dfrac{x}{y})^n = \dfrac{x^n}{y^n}, y \not = 0$