3.5: Subtraction of Signed Numbers
- Page ID
- 49358
Overview
- Definition of Subtraction
- Subtraction of Signed Numbers
Definition of Subtraction
We know from our experience with arithmetic that the subtraction \(5−2\) produces \(3\), that is, \(5−2=3\). Illustrating this process on the number line suggests a rule for subtracting signed numbers.

We begin at \(0\), the origin.
Since \(5\) is positive, we move \(5\) units to the right.
Then, we move 2 units to the left to get to \(3\). (This reminds us of addition with a negative number.)
This illustration suggests that \(5−2\) is the same as \(5+(−2)\).
This leads us directly to the definition of subtraction.
If \(a\) and \(b\) are real numbers, \(a−b\) is the same as \(a+(−b)\), where \(−b\) is the opposite of \(b\).
Subtraction of Signed Numbers
The preceding definition suggests the rule for subtracting signed numbers.
To perform the subtraction \(a−b\), add the opposite of \(b\) to \(a\), that is, change the sign of \(b\) and add.
Sample Set A
Perform the subtractions.
\(5−3=5+(−3)=2\)
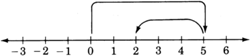
\(4−9=4+(−9)=−5\)

\(−4−6=−4+(−6)=−10\)

\(−3−(−12)=−3+12=9\)

\(0−(−15)=0+15=15\)

The high temperature today in Lake Tahoe was 26F. The low temperature tonight is expected to be −7F. How many degrees is the temperature expected to drop?
We need to find the difference between 26 and −7.
\(26−(−7)=26+7=33\)
Thus, the expected temperature drop is 33F.
\(\begin{aligned}
-6-(-5)-10 &=-6+5+(-10) \\
&=(-6+5)+(-10) \\
&=-1+(-10) \\
&=-11
\end{aligned}\)
Practice Set A
Perform the subtractions.
\(9−6\)
- Answer
-
\(3\)
\(6-9\)
- Answer
-
\(-3\)
\(0-7\)
- Answer
-
\(-7\)
\(1-14\)
- Answer
-
\(-13\)
\(-8-12\)
- Answer
-
\(-20\)
\(-21-6\)
- Answer
-
\(-27\)
\(-6-(-4)\)
- Answer
-
\(-2\)
\(8-(-10)\)
- Answer
-
\(18\)
\(1-(-12)\)
- Answer
-
\(13\)
\(86-(-32)\)
- Answer
-
\(118\)
\(0-16\)
- Answer
-
\(-16\)
\(0-(-16)\)
- Answer
-
\(16\)
\(0-(8)\)
- Answer
-
\(-8\)
\(5-(-5)\)
- Answer
-
\(10\)
\(24-(-(-24))\)
- Answer
-
\(0\)
Exercises
For the following exercises, perform the indicated operations.
\(8-3\)
- Answer
-
\(5\)
\(12 - 7\)
- Answer
-
\(5\)
\(5-6\)
- Answer
-
\(-1\)
\(14 - 30\)
\(2 - 15\)
- Answer
-
\(-13\)
\(5 - 18\)
- Answer
-
\(-13\)
\(1 - 7\)
- Answer
-
\(-6\)
\(4 - 11\)
\(-6 - 5\)
- Answer
-
\(-11\)
\(-8 - 14\)
\(-1 - 12\)
- Answer
-
\(-13\)
\(-4 - 4\)
\(-6 - 8\)
- Answer
-
\(-14\)
\(-1 - 12\)
- Answer
-
\(-13\)
\(-5 - (-3)\)
- Answer
-
\(-2\)
\(-11 - (-8)\)
\(-7 -(-12)\)
- Answer
-
\(5\)
\(-2 -(-10)\)
\(-4 -(-15)\)
- Answer
-
\(11\)
\(-11 -(-16)\)
\(-1 -(-6)\)
- Answer
-
\(5\)
\(-8 -(-14)\)
\(-15 -(-10)\)
- Answer
-
\(-5\)
\(-11 -(-4)\)
\(-16 -(-8)\)
- Answer
-
\(-8\)
\(-12 -(-11)\)
\(0 - 6\)
- Answer
-
\(-6\)
\(0 - 15\)
\(0 - (-7)\)
- Answer
-
\(7\)
\(0 - (-10)\)
\(67 - 38\)
- Answer
-
\(29\)
\(142 - 85\)
\(816 - 1140\)
- Answer
-
\(-324\)
\(105-421\)
\(-550 - (-121)\)
- Answer
-
\(-429\)
\(−15.016−(4.001)\)
\(−26+7−52\)
- Answer
-
\(-71\)
\(−15−21−(−2)\)
\(−104−(−216)−(−52)\)
- Answer
-
\(164\)
\(−0.012−(−0.111)−(0.035)\)
\([5+(−6)]−[2+(−4)]\)
- Answer
-
\(1\)
\([2+(−8)]−[5+(−7)]\)
\([4+(−11)]−[2+(−10)]\)
- Answer
-
\(1\)
\([9+(−6)]−[4+(−12)]\)
\((11−8)−(1−6)\)
- Answer
-
\(8\)
\((5−12)−(4−10)\)
\((1−10)−(2−15)\)
- Answer
-
\(4\)
\((0−8)−(4−12)\)
\((−4+7)−(2−5)\)
- Answer
-
\(6\)
\((−6+2)−(5−11)\)
\([−8+(−5+3)]−[9−(−3−5)]\)
- Answer
-
\(-27\)
\([−4+(−1+6)]−[7−(−6−1)]\)
\([2−(−6+10)]−[1−(2−11)]\)
- Answer
-
\(-12\)
\([5−(−2−5)]−[2−(−1−4)]\)
When a particular machine is operating properly, its meter will read 34. If a broken bearing in the machine causes the meter reading to drop by 45 units, what is the meter reading?
- Answer
-
\(-11\)
The low temperature today in Denver was −4F and the high was 42F. What is the temperature difference?
Exercises for Review
Use the distributive property to expand \(4x(5y+11)\)
- Answer
-
\(20xy + 44x\)
Simplify \(\dfrac{2(3x^2y^2)^3(2x^4y^3)^0}{27x^4y^3}\). Assume \(x \not = 0\), \(y \not = 0\)
Simplify \(|-(4^2+2^2-3^2)|\).
- Answer
-
\(11\)
Find the sum. \(-8 + (-14)\)
Find the sum. \(3 + (-6)\).
- Answer
-
\(-3\)


