5.6: Application II - Solving Problems
- Page ID
- 49371
Solving Applied Problems
Let’s study some interesting problems that involve linear equations in one variable. In order to solve such problems, we apply the following five-step method:
Five-Step Method for Solving Word Problems
- Let \(x\) (or some other letter) represent the unknown quantity.
- Translate the words to mathematical symbols and form an equation.
- Solve this equation.
- Ask yourself "Does this result seem reasonable?" Check the solution by substituting the result into the original statement of the problem.
If the answer doesn’t check, you have either solved the equation incorrectly, or you have developed the wrong equation. Check your method of solution first. If the result does not check, reconsider your equation.
- Write the conclusion.
If it has been your experience that word problems are difficult, then follow the five-step method carefully. Most people have difficulty because they neglect step 1.
Always start by INTRODUCING A VARIABLE!
Keep in mind what the variable is representing throughout the problem.
Sample Set A
This year an item costs $44, an increase of $3 over last year's price. What was last year's price?
\(\begin{array}{flushleft}
\text{Step 1: }\text{Let }x&=&\text{last year's price}\\
\text{Step 2: }x+3&=&44&x+3\text{ represents the \$3 increase in price.}\\
\text{Step 3: }&x+3&=&44\\
&x+3-3&=&44-3\\
&x&=&41\\
\text{Step 4: }&41+3&=&44&\text{Yes, this is correct}\\
\text{Step 5: Last year's price was \$41}.
\end{array}\)
Practice Set A
This year an item costs $23, an increase of $4 over last year’s price. What was last year’s price?
- Let \(x=\)
- Last year's price was .
- Answer
-
Last year's price was $19
Sample Set B
The perimeter (length around) of a square is 60 cm (centimeters). Find the length of a side.
Step 1: Let \(x = \text{ length of a side.}\).
Step 2: We can draw a picture.
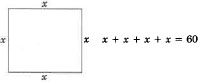
\(\begin{array}{flushleft}
\text{Step 3: }&x+x+x+x&=&60\\
&4x&=&60&\text{Divide both sides by 4.}\\
&x&=&15\\
\text{Step 4: }&4(15)&=&60&\text{Yes, this is correct}\\
\text{Step 5: }&\text{The length of a side is 15 cm}
\end{array}\)
Practice Set B
The perimeter of a triangle is 54 inches. If each side has the same length, find the length of a side.
- Let \(x=\)
- The length of a side is inches.
- Answer
-
The length of a side is 18 inches.
Sample Set C
Six percent of a number is 54. What is the number?
\(\begin{array}{flushleft}
\text{Step 1: }&\text{Let } x = \text{the number}\\
\text{Step 2: }&\text{We must convert 6% to a decimal}\\
\end{array}\)
\(\begin{array}{flushleft}
&6\%&=&.06\\
&.06x&=&54&.06x\text{ occurs because we want 6% of } x.\\
\text{Step 3: }&.06x&=&54&\text{Divide both sides by } .06.\\
&x&=&\dfrac{54}{.06}\\
&x&=&900\\
\text{Step 4: }&.06(900)&=&54.&\text{Yes, this is correct.}\\
\text{Step 5: }&\text{The number is } 900.
\end{array}\)
Practice Set C
Eight percent of a number is 36. What is the number?
- Let \(x=\)
- The number is .
- Answer
-
The number is 450.
Sample Set D
An astronomer notices that one star gives off about 3.6 times as much energy as another star. Together the stars give off 55.844 units of energy. How many units of energy does each star emit?
1. In this problem we have two unknowns and, therefore, we might think, two variables. However, notice that the energy given off by one star is given in terms of the other star. So, rather than introducing two variables, we introduce only one. The other unknown(s) is expressed in terms of this one. (We might call this quantity the base quantity.)
Let \(x=\) number of units of energy given off by the less energetic star. Then, \(3.6x=\) number of units of energy given off by the more energetic star.
\(\begin{array}{flushleft}
\text{Step 2: }&x+3.6x&=&55.844\\
\text{Step 3: }&x+3.6x&=&55.844\\
&4.6x&=&55.844&\text{Divide both sides by } 4.6 \text{. A calculator would be useful at this point.}\\
&x&=&\dfrac{55.844}{4.6}\\
&x&=&12.14&\text{The wording of the problem implies two numbers are needed }\\
&&&&\text{for a complete solution. We need the number of units of}\\
&&&&\text{energy for the other star.}\\
&3.6x&=&3.6(12.14)\\
&&=&43.704\\
\text{Step 4: }&12.14+43.704&=&55.844&\text{Yes, this is correct}.
\end{array}\)
\(\text{Step 5: One start gives off } 12.14 \text{ units of energy and the other star gives off } 43.704 \text{ units of energy}\)
Practice Set D
Garden A produces 5.8 times as many vegetables as garden B. Together the gardens produce 102 pounds of vegetables. How many pounds of vegetables does garden A produce?
- Let \(x =\)
- Answer
-
Garden A produces 87 pounds of vegetables.
Sample Set E
Two consecutive even numbers sum to 432. What are the two numbers?
\(\text{Step 1: Let } x= \text{ the smaller even number. Then } x+2= \text{ the next (consecutive) even number}\\
\text{since consecutive even numbers differ by } 2 \text{ (as do consecutive odd numbers) }\)
\(\begin{array}{flushleft}
\text{Step 2: }&x+x+2&=&432\\
\text{Step 3: }&x+x+2&=&432\\
&2x+2&=&432\\
&2x&=&430\\
&x&=&215&\text{Also, since } x=215, x+2=217
\end{array}\)
\(\text{Step 4: }215+217=432, \text{ but } 215 \text{ and } 217 \text{ are odd numbers and we are looking for even numbers.}\\
\text{Upon checking our method of solution and reexamining our equation, we find no}\\
\text{mistakes.}\)
\(\text{Step 5: We must conclude that this problem has no solution. There are no two consecutive even numbers that sum to 432}\)
Practice Set E
The sum of two consecutive even numbers is 498. What are the two numbers?
- Answer
-
The two numbers are 248 and 250.
Exercises
Solve the following problems. Note that some of the problems may seem to have no practical applications and may not seem very interesting. They, along with the other problems, will, however, help to develop your logic and problem-solving ability.
If eighteen is subtracted from some number the result is fifty-two. What is the number?
- Let \(x=\)
- The equation is
- (Solve the equation.)
- (Check)
- The number is .
- Answer
-
Step 1: Let \(x =\) the unknown quantity.
Step 2: The equation is \(x−18=52\).
Step 3: (Solve the equation.) Add 18 to each side.
\( x−18+18=52+18\\
x=70\)
Step 4: (Check) \(70−18=52\); True.
Step 5: The number is 70.
If nine more than twice a number is forty-six, what is the number?
- Let \(x=\)
- The equation is
- (Solve the equation.)
- (Check)
- The number is.
If nine less than three eighths of a number is two and one fourth, what is the number?
- Let \(x=\)
- The number is .
- Answer
-
Step 5: The number is 30.
Twenty percent of a number is 68. What is the number?
- Let \(x=\)
- The number is .
Eight more than a quantity is 37. What is the original quantity?
- Let \(x=\)
- The original quantity is .
- Answer
-
Step 5: The original quantity is 29.
If a quantity plus 85% more of the quantity is 62.9, what is the original quantity?
- Let x= original quantity.
- The original quantity is.
A company must increase production by 12% over last year’s production. The new output will be 56 items. What was last year’s output?
- Let \(P=\)
- Last year’s output was items.
- Answer
-
Step 5: Last year's output was 50 items.
A company has determined that it must increase production of a certain line of goods by \(1\dfrac{1}{2}\) times last year’s production. The new output will be 2885 items. What was last year’s output?
- Last year’s output was items.
A proton is about 1837 times as heavy as an electron. If an electron weighs 2.68 units, how many units does a proton weigh?
- A proton weighs units.
- Answer
-
Step 5: A proton weighs 4923.16 units.
Three consecutive integers sum to 36. What are they?
- Answer
-
Step 5: The first integer is 11; second is 12; third is 13.
Neptune is about 30 times as far from the sun as is the Earth. If it takes light 8 minutes to travel from the sun to the Earth, how many minutes does it take to travel to Neptune?
- Light takes minutes to reach Neptune.
The radius of the sun is about 695,202 km (kilometers). That is about 109 times as big as the radius of the Earth. What is the radius of the earth?
- The radius of the earth is km.
- Answer
-
Step 5: The radius of the earth is 6378 km.
Three consecutive even integers add up to 131. What are they?
The perimeter of a triangle is 105 cm. If each of the two legs is exactly twice the length of the base, how long is each leg?
- Let \(=\)
Draw a picture. - Each leg is cm long. The base is .
A lumber company has contracted to cut boards into two pieces so that one piece is three times the length of the other piece. If a board is 12 feet long, what is the length of each piece after cutting?
- The length of the shorter piece is feet, and the length of the longer piece is feet.
- Answer
-
Step 5: The length of the shorter piece is 3 feet, and the length of the longer piece is 9 feet.
Two consecutive odd integers sum to 151. What are they?
A student doing a chemistry experiment has a beaker that contains 84 ml (milliliters) of an alcohol and water solution. Her lab directions tell her that there is 4.6 times as much water as alcohol in the solution. How many milliliters of alcohol are in the solution? How many milliliters of water?
- There are ml of alcohol in the solution. There are ml of water in the solution.
A statistician is collecting data to help him estimate the average income of accountants in California. He needs to collect 390 pieces of data and he is \(\dfrac{2}{3}\) done. How many pieces of data has the statistician collected?
- The statistician has collected pieces of data.
Suppose the statistician is 4 pieces of data short of being \(\dfrac{2}{3}\) done. How many pieces of data has he collected?
- Answer
-
Step 5: The statistician has collected 260 pieces of data.
A television commercial advertises that a certain type of battery will last, on the average, 20 hours longer than twice the life of another type of battery. If consumer tests show that the advertised battery lasts 725 hours, how many hours must the other type of battery last for the advertiser’s claim to be valid?
- The other type of battery must last hours for the advertiser’s claim to be valid.
A 1000-ml flask containing a chloride solution will fill 3 beakers of the same size with 210 ml of the solution left over. How many milliliters of the chloride solution will each beaker hold?
- Each beaker will hold ml of the chloride solution.
- Answer
-
Step 5: Each beaker will hold \(263\dfrac{1}{3}\) ml of chloride solution.
A star burns \(\dfrac{2}{9}\) of its original mass then blows off \(\dfrac{3}{7}\) of the remaining mass as a planetary nebula. If the final mass is 3 units of mass, what was the original mass?
- The original mass was units of mass.
The sum of a number and sixteen is forty-two. What is the number?
- Answer
-
Step 5: The unknown number is 26.
When eleven is subtracted from a number, the result is 85. What is the number?
Three times a number is divided by 6 and the result is 10.5. What is the number?
- Answer
-
Step 5: The unknown number is 21.
When a number is multiplied by itself, the result is 144. What is the number?
A number is tripled, then increased by seven. The result is 48. What is the number?
- Answer
-
Step 5: The unknown number is \(\dfrac{41}{3}\).
Eight times a number is decreased by three times the number, giving a difference of 22. What is the number?
One number is fifteen more than another number. The sum of the two numbers is 27. What are they?
- Answer
-
Step 5: One unknown number is 6; the other is 21.
The length of a rectangle is 6 meters more than three times the width. The perimeter of the rectangle is 44 meters What are the dimensions of the rectangle?
Seven is added to the product of 41 and some number. The result, when divided by four, is 63. What is the number?
- Answer
-
Step 5: The unknown number is \(\dfrac{245}{41}\).
The second side of a triangle is five times the length of the smallest side. The third is twice the length of the second side. The perimeter of the triangle is 48 inches. Find the length of each side.
Person A is four times as old as person B, who is six times as old as person C, who is twice as old as person D. How old is each person if their combined ages are 189 months?
As a consequence of Einstein’s theory of relativity, the rate of time passage is different for a person in a stationary position and a person in motion. (Hard to believe, but true!) To the moving observer, the rate of time passage is slower than that of the stationary observer, that is, the moving person ages slower than the stationary observer. (This fact has been proven many times by experiments with radioactive materials.) The effect is called “time dilation” and is really only noticeable when an object is traveling at near the speed of light (186,000 miles per second). Considering these ideas, try to solve the following problems:
Two people have identical clocks. One is standing on the earth and the other is moving in a spacecraft at 95% the speed of light, 176,700 miles per second. The moving person’s rate of time passage at this speed is about 0.31 times as fast as the person standing on earth.
- If two days of earth time pass, how many days actually pass on the spacecraft?
- If 30 years of earth time pass, how many years have actually passed on the spacecraft?
- years have passed on the spacecraft.
- If 30 years have passed on the spacecraft, how many years have passed on the earth?
- A space traveler makes a round-trip voyage to the star Capella. The trip takes her 120 years (traveling at 176,000 miles per second). If it is the year 2000 on earth when she leaves, what earth year will it be when she returns?
- Answer
-
(a) Step 5: The time passed in space is 0.62 days.
(b) Step 5: 9.3 years have passed on the spacecraft.
(c) Step 5: 96.77 years have passed on the earth.
(d) Step 5: Earth year when she returns will be 2387.
Exercises for Review
Specify the domain of the equation \(y = \dfrac{x-1}{x+4}\)
Classify the equation \(x+4=1\) as an identity, a contradiction, or a conditional equation.
- Answer
-
conditional
Classify the equation \(2x+3=2x+3\) as an identity, a contradiction or a conditional equation.
Solve the equation \(4(x−1)+12=−3(2x+4)\).
- Answer
-
\(x=−2\)
Translate the following sentence to a mathematical equation. Three less than an unknown number is multiplied by negative four. The result is two more than the original unknown number.


