5.8: Linear Equations in Two Variables
- Page ID
- 58540
Solutions to Linear Equations in Two Variables
Solution to an Equation in Two Variables
We have discovered that an equation is a mathematical way of expressing the relationship of equality between quantities. If the relationship is between two quantities, the equation will contain two variables. We say that an equation in two variables has a solution if an ordered pair of values can be found such that when these two values are substituted into the equation a true statement results. This is illustrated when we observe some solutions to the equation \(y=2x+5\).
\(\begin{array}{l}
x=4, y=13 ; \quad \text { since } 13=2(4)+5 \text { is true } \\
x=1, y=7 ; \quad \text { since } 7=2(1)+5 \text { is true. } \\
x=0, y=5 ; \quad \text { since } 5=2(0)+5 \text { is true. } \\
x=-6, y=-7 ; \quad \text { since }-7=2(-6)+5 \text { is true. }
\end{array}\)
Ordered Pairs as Solutions
It is important to keep in mind that a solution to a linear equation in two variables is an ordered pair of values, one value for each variable. A solution is not completely known until the values of both variables are specified.
Independent and Dependent Variables
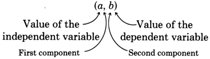
Recall that, in an equation, any variable whose value can be freely assigned is said to be an independent variable. Any variable whose value is determined once the other value or values have been assigned is said to be a dependent variable. If, in a linear equation, the independent variable is x and the dependent variable is y, and a solution to the equation is x=a and y=b, the solution is written as the
ORDERED PAIR: \((a, b)\)
Ordered Pair
In an ordered pair, \((a, b)\), the first component, \(a\), gives the value of the independent variable, and the second component, \(b\), gives the value of the dependent variable.
We can use ordered pairs to show some solutions to the equation \(y=6x−7\).
\((0, -7)\)
If \(x = 0\) and \(y = -7\), we get a true statement upon substitution and computation
\(\begin{array}{flushleft}
y&=&6x-7\\
-7&=&6(0)-7&\text{Is this correct?}\\
-7&=&-7&\text{Is this correct?}\\
-7&=&41&\text{Yes, this is correct}
\end{array}\)
\((8, 41)\)
If \(x = 8\) and \(y = 41\), we get a true statement upon substitution and computation
\(\begin{array}{flushleft}
y&=&6x-7\\
41&=&6(8)-7&\text{Is this correct?}\\
41&=&48-7&\text{Is this correct?}\\
41&=&41&\text{Yes, this is correct}
\end{array}\)
\((-4, -31)\)
If \(x = 8\) and \(y = 41\), we get a true statement upon substitution and computation
\(\begin{array}{flushleft}
y&=&6x-7\\
-31&=&6(-4)-7&\text{Is this correct?}\\
-31&=&-24-7&\text{Is this correct?}\\
-31&=&-31&\text{Yes, this is correct}
\end{array}\)
These are only three of the infintely many solutions to this equation.
Sample Set A
Find a solution to each of the following linear equations in two variables and write the solution as an ordered pair.
\(
y=3 x-6, \text { if } x=1
\)
Substitute 1 for \(x\), compute, and solve for \(y\).
\(
\begin{aligned}
y &=3(1)-6 \\
&=3-6 \\
&=-3
\end{aligned}
\)
Hence, one solution is \((1,-3)\).
\(
y=15-4 x, \text { if } x=-10
\)
Substitute -10 for \(x\), compute, and solve for \(y\).
\(
\begin{aligned}
y &=15-4(-10) \\
&=15+40 \\
&=55
\end{aligned}
\)
Hence, one solution is \((-10,55)\).
\(
b=-9 a+21, \text { if } a=2
\)
Substitute 2 for \(a\), compute, and solve for \(b\).
\(
\begin{aligned}
b &=-9(2)+21 \\
&=-18+21 \\
&=3
\end{aligned}
\)
Hence, one solution is \((2,3)\).
\(5 x-2 y=1, \text{ if } x=0\)
Substitute 0 for \(x\), compute, and solve for \(y\).
\(
\begin{aligned}
5(0)-2 y &=1 \\
0-2 y &=1 \\
-2 y &=1 \\
y &=-\dfrac{1}{2}
\end{aligned}
\)
Hence, one solution is \(\left(0,-\dfrac{1}{2}\right)\).
Practice Set A
Find a solution to each of the following linear equations in two variables and write the solution as an ordered pair.
\(y=7x−20\), if \(x=3\)
- Answer
-
\((3, 1)\)
\(m=−6n+1\), if \(n=2\)
- Answer
-
\((2, −11)\)
\(b=3a−7\), if \(a=0\)
- Answer
-
\((0, −7)\)
\(10x−5y−20=0\), if \(x=−8\)
- Answer
-
\((−8, −20)\)
\(3a+2b+6=0\), if \(a=−1\)
- Answer
-
\((-1, \dfrac{-3}{2})\)
Exercises
For the following problems, solve the linear equations in two variables.
\(y=8x+14\), if \(x=1\)
- Answer
-
\((1,22)\)
\(y=−2x+1\), if \(x=0\)
\(y=5x+6\), if \(x=4\)
- Answer
-
\((4,26)\)
\(x+y=7\), if \(x=8\)
\(3x+4y=0\), if \(x=−3\)
- Answer
-
\((-3, \dfrac{9}{4})\)
\(−2x+y=1\), if \(x=\dfrac{1}{2}\)
\(5x−3y+1=0\), if \(x=−6\)
- Answer
-
\((-6, -\dfrac{29}{3})\)
\(−4x−4y=4\), if \(y=7\)
\(2x+6y=1\), if \(y=0\)
- Answer
-
\((\dfrac{1}{2}, 0)\)
\(−x−y=0\), if \(y=\dfrac{14}{3}\)
\(y=x\), if \(x=1\)
- Answer
-
\((1,1)\)
\(x+y=0\), if \(x=0\)
\(y + \dfrac{3}{4} = x\), if \(x = \dfrac{9}{4}\)
- Answer
-
\((\dfrac{9}{4}, \dfrac{3}{2})\)
\(y+17=x\), if \(x=−12\)
\(−20y+14x=1\), if \(x=8\)
- Answer
-
\((8, \dfrac{111}{20})\)
\(\dfrac{3}{5}y + \dfrac{1}{4}x = \dfrac{1}{2}\), if \(x = -3\)
\(\dfrac{1}{5}x + y = -9\), if \(y = -1\).
- Answer
-
\((−40,−1)\)
\(y+7−x=0\), if \(x = *\)
\(2x+31y−3=0\), if \(x=a\)
- Answer
-
\((a, \dfrac{3-2a}{31})\)
\(436x+189y=881\), if \(x=−4231\)
\(y=6(x−7)\), if \(x=2\)
- Answer
-
\((2,−30)\)
\(y=2(4x+5)\), if \(x=−1\)
\(5y=9(x−3)\), if \(x=2\)
- Answer
-
\((2, -\dfrac{9}{5})\)
\(3y=4(4x+1)\), if \(x=−3\)
\(−2y=3(2x−5)\), if \(x=6\)
- Answer
-
\((6, -\dfrac{21}{2})\)
\(−8y=7(8x+2)\), if \(x=0\)
\(b=4a−12\), if \(a=−7\)
- Answer
-
\((−7,−40)\)
\(b=−5a+21\), if \(a=−9\)
\(4b−6=2a+1\), if \(a=0\)
- Answer
-
\((0, \dfrac{7}{4})\)
\(−5m+11=n+1\), if \(n=4\)
\(3(t+2)=4(s−9)\), if \(s=1\)
- Answer
-
\((1, -\dfrac{38}{3})\)
\(7(t−6)=10(2−s)\), if \(s=5\)
\(y=0x+5\), if \(x=1\)
- Answer
-
\((1,5)\)
\(2y=0x−11\), if \(x=−7\)
\(−y=0x+10\), if \(x=3\)
- Answer
-
\((3,−10)\)
\(−5y=0x−1\), if \(x=0\)
\(y=0(x−1)+6\), if \(x=1\)
- Answer
-
\((1,6)\)
\(y=0(3x+9)−1\), if \(x=12\)
An examination of the winning speeds in the Indianapolis 500 automobile race from 1961 to 1970 produces the equation \(y=1.93x+137.60\), where \(x\) is the number of years from 1960 and \(y\) is the winning speed. Statistical methods were used to obtain the equation, and, for a given year, the equation gives only the approximate winning speed. Use the equation \(y=1.93x+137.60\) to find the approximate winning speed in
- 1965
- 1970
- 1986
- 1990
- Answer
-
(a) Approximately 147 mph using \((5,147.25)\)
(b) Approximately 157 mph using \((10,156.9)\)
(c) Approximately 188 mph using \((26,187.78)\)
(d) Approximately 196 mph using \((30,195.5)\)
In electricity theory, Ohm’s law relates electrical current to voltage by the equation \(y=0.00082x\), where \(x\) is the voltage in volts and \(y\) is the current in amperes. This equation was found by statistical methods and for a given voltage yields only an approximate value for the current. Use the equation \(y=0.00082x\) to find the approximate current for a voltage of
- 6 volts
- 10 volts
Statistical methods have been used to obtain a relationship between the actual and reported number of German submarines sunk each month by the U.S. Navy in World War II. The equation expressing the approximate number of actual sinkings, \(y\), for a given number of reported sinkings, \(x\), is \(y=1.04x+0.76\). Find the approximate number of actual sinkings of German submarines if the reported number of sinkings is
- 4
- 9
- 10
- Answer
-
(a) Approximately 5 sinkings using \((4,4.92)\)
(b) Approximately 10 sinkings using \((9,10.12)\)
(c) Approximately 11 sinkings using \((10,11.16)\)
Statistical methods have been used to obtain a relationship between the heart weight (in milligrams) and the body weight (in milligrams) of 10-month-old diabetic offspring of crossbred male mice. The equation expressing the approximate body weight for a given heart weight is \(y=0.213x−4.44\). Find the approximate body weight for a heart weight of
- 210 mg
- 245 mg
Statistical methods have been used to produce the equation \(y=0.176x−0.64\). This equation gives the approximate red blood cell count (in millions) of a dog’s blood, \(y\), for a given packed cell volume (in millimeters), \(x\). Find the approximate red blood cell count for a packed cell volume of
- 40 mm
- 42 mm
- Answer
-
(a) Approximately 6.4 using \((40,6.4)\)
(b) Approximately 4.752 using \((42,7.752)\)
An industrial machine can run at different speeds. The machine also produces defective items, and the number of defective items it produces appears to be related to the speed at which the machine is running. Statistical methods found that the equation \(y=0.73x−0.86\) is able to give the approximate number of defective items, \(y\), for a given machine speed, \(x\). Use this equation to find the approximate number of defective items for a machine speed of
- 9
- 12
A computer company has found, using statistical techniques, that there is a relationship between the aptitude test scores of assembly line workers and their productivity. Using data accumulated over a period of time, the equation \(y=0.89x−41.78\) was derived. The \(x\) represents an aptitude test score and \(y\) the approximate corresponding number of items assembled per hour. Estimate the number of items produced by a worker with an aptitude score of
- 80
- 95
- Answer
-
(a) Approximately 29 items using \((80,29.42)\)
(b) Approximately 43 items using \((95,42.77)\)
Chemists, making use of statistical techniques, have been able to express the approximate weight of potassium bromide, \(W\), that will dissolve in 100 grams of water at \(T\) degrees centigrade. The equation expressing this relationship is \(W=0.52T+54.2\). Use this equation to predict the potassium bromide weight that will dissolve in 100 grams of water that is heated to a temperature of
- 70 degrees centigrade
- 95 degrees centigrade
The marketing department at a large company has been able to express the relationship between the demand for a product and its price by using statistical techniques. The department found, by analyzing studies done in six different market areas, that the equation giving the approximate demand for a product (in thousands of units) for a particular price (in cents) is \(y=−14.15x+257.11\). Find the approximate number of units demanded when the price is
- $0.12
- $0.15
- Answer
-
(a) Approximately 87 units using \((12,87.31)\)
(b) Approximately 45 units using \((15,44.86)\)
The management of a speed-reading program claims that the approximate speed gain (in words per minute), \(G\), is related to the number of weeks spent in its program, \(W\), is given by the equation \(G=26.68W−7.44\). Predict the approximate speed gain for a student who has spent
- 3 weeks in the program
- 10 weeks in the program
Exercises for Review
Find the product. \((4x−1)(3x+5)\).
- Answer
-
\(12x^2+17x−5\)
Find the product. \((5x+2)(5x−2)\)
Solve the equation \(6[2(x−4)+1]=3[2(x−7)]\).
- Answer
-
\(x=0\)
Solve the inequality \(−3a−(a−5)≥a+10\).
Solve the compound inequality \(−1<4y+11<27\).
- Answer
-
\(−3<y<4\)


