6.8: Factoring Trinomials with Leading Coefficient Other Than 1
- Page ID
- 49379
The Method of Factorization
In the last section we saw that we could easily factor trinomials of the form \(x^2+bx+c\) by finding the factors of the constant \(c\) that add to the coefficient of the linear term \(b\), as shown in the following example:
Factor \(x^2 - 4x - 21\)
The third term of the trinomial is \(-21\). We seek two numbers whose:
(a) product is \(-21\)
(b) sum is \(-4\)
The required numbers are \(-7\) and \(+3\)
\(x^2 - 4x - 21 = (x-7)(x+3)\)
The problem of factoring the polynomial \(ax^2 + bx + c, a\not = 1\), becomes more involved. We will study two methods of factoring such polynomials. Each method produces the same result, and you should select the method you are most comfortable with. The first method is called the trial and error method and requires some educated guesses. We will examine two examples (Sample Sets A and B). Then, we will study a second method of factoring. The second method is called the collect and discard method, and it requires less guessing than the trial and error method. Sample Set C illustrates the use of the collect and discard method.
The Trial and Error Method of Factoring \(ax^2 + bx + c\)
Trial and Error Method
Consider the product
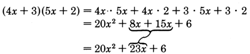
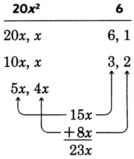
Examining the trinomial \(20x^2 + 23x + 6\), we can immediately see some factors of the first and last terms.
| \(20x^2\) | \(6\) |
| \(20x, x\) | \(6, 1\) |
| \(10x, 2x\) | \(3, 2\) |
| \(5x, 4x\) |
Our goal is to choose the proper combination of factors of the first and last terms that yield the middle term \(23x\).
Notice that the middle term comes from the sum of the outer and inner products in the multiplication of the two binomials.
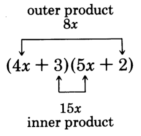
This fact provides us a way to find the proper combination.
Look for the combination that when multiplied and then added yields the middle term.
The proper combination we're looking for is
Sample Set A
Factor \(6x^2 + x - 12\)
Factor the first and last terms:
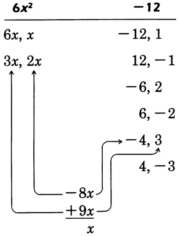
Thus, \(3x\) and \(3\) are to be multiplied, \(2x\) and \(-4\) are to be multiplied.
\(\begin{array}{flushleft}
6x^2 + x - 12&=&( ) ( )&\text{Put the factors of the leading term in immediately.}\\
&=&(3x)(2x)&\text{Since } 3x \text{ and } 3 \text{ are to be multiplied, they must be located in different binomials.}\\
&=&(3x)(2x + 3)&\text{Place the } -4 \text{ in the remaining set of parentheses.}\\
&=&(3x-4)(2x+3)\\
6x^2 + x - 12&=&(3x-4)(2x+3)
\end{array}\)
Check:
\(\begin{array}{flushleft}
(3x-4)(2x+3)&=&6x^2 + 9x - 8x - 12\\
&=&6x^2 + x - 12
\end{array}\)
Factor \(8x^2 - 20x - 27\)
Find the factors of the first and last terms.
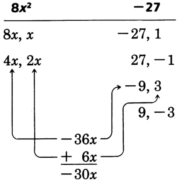
Thus, the \(4x\) and \(-9\) are to be multiplied, and \(2x\) and \(3\) are to be multiplied.
\(\begin{array}{flushleft}
8x^2 - 30x - 27&=& (4x)(2x)\\
&=&(4x)(2x-9)\\
&=&(4x + 3)(2x-9)
\end{array}\)
Check:
\(\begin{array}{flushleft}
(4x+3)(2x-9)&=&8x^2 - 36x + 6x - 27\\
&=&8x^2-30x-27
\end{array}\)
Factor \(15x^2 + 44x + 32\)
Before we start finding the factors of the first and last terms, notice that the constant term is \(+32\). Since the product is positive, the two factors we are looking for must have the same sign. They must both be positive or both be negative. Now the middle term, \(+44x\), is preceded by a positive sign. We know that the middle term comes from the sum of the outer and inner products. If these two numbers are to sum to a positive number, they must both be positive themselves. If they were negative, their sum would be negative. Thus, we can conclude that the two factors of \(+32\) that we are looking for are both positive numbers. This eliminates several factors of \(32\) and lessens our amount of work.
Factor the first and last terms.
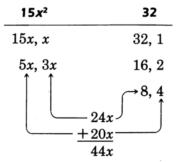
After a few trials we see that \(5x\) and \(4\) are to be multiplied, and \(3x\) and \(8\) are to be multiplied.
\(15x^2 + 44x + 32 = (5x + 8)(3x + 4)\)
Factor \(18x^2 - 56x + 6\)
We see that each term is even, so we can factor out \(2\).
\(2(9x^2 - 28x + 3)\)
Notice that the constant term is positive. Thus, we know that the factors of 3 that we are looking for must have the same sign. Since the sign of the middle term is negative, both factors must be negative.
Factor the first and last terms.
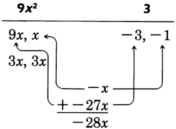
There are not many combinations to try, and we find that \(9x\) and \(-3\) are to be multiplied and \(x\) and \(-1\) are to be multiplied.
\(\begin{array}{flushleft}
18x^2 - 56x + 6 &=& 2(9x^2 - 28x + 3)\\
&=&2(9x-1)(x-3)
\end{array}\)
If we had not factored out the \(2\) first, we would have gotten the factorization
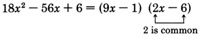
The factorization is not complete since one of the factors may be factored further.
\(\begin{array}{flushleft}
18x^2 - 56x + 6&=&(9x-1)(2x-6)\\
&=&(9x-1)\cdot 2(x-3)\\
&=&2(9x-1)(x-3)&\text{(By the commutative property of multiplication)\)
\end{array}\)
The results are the same, but it is much easier to factor a polynomial after all common factors have been factored out first.
Factor \(3x^2 + x - 14\)
There are no common factors. We see that the constant term is negative. Thus, the factors of \(-14\) must have different signs. Factor the first and last terms.
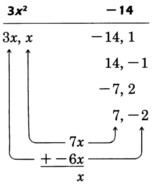
After a few trials, we see that \(3x\) and \(-2\) are to be multiplied.
\(3x^2 + x - 14 = (3x + 7)(x - 2)\)
Factor \(8x^2 - 26xy + 15y^2\).
We see that the constant term is positive and that the middle term is preceded by a minus sign.
Hence, the factors of \(15y^2\) that we are looking for must both be negative.
Factor the first and last terms.
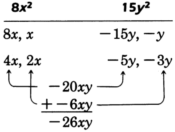
After a few trials, we see that \(4x\) and \(-5y\) are to be multiplied and \(2x\) and \(-3y\) are to be multiplied.
\(8x^2 - 26xy + 15y^2 = (4x - 3y)(2x - 5y)\)
Practice Set A
Factor the following, if possible.
\(2x^2+13x−7\)
- Answer
-
\((2x−1)(x+7)\)
\(3x^2+x−4\)
- Answer
-
\((3x+4)(x−1)\)
\(4a^2−25a−21\)
- Answer
-
\((4a+3)(a−7)\)
\(16b^2−22b−3\)
- Answer
-
\((8b+1)(2b−3)\)
\(10y^2−19y−15\)
- Answer
-
\((5y+3)(2y−5)\)
\(6m^3+40m^2−14m\)
- Answer
-
\(2m(3m−1)(m+7)\)
\(14p^2+31pq−10q^2\)
- Answer
-
\((7p−2q)(2p+5q)\)
\(−24w^2z^2+14wz^3−2z^4\)
- Answer
-
\(−2z^2(4w−z)(3w−z)\)
\(3x^2+6xy+2y^2\)
- Answer
-
not factorable
As you get more practice factoring these types of polynomials you become faster at picking the proper combinations. It takes a lot of practice!
There is a shortcut that may help in picking the proper combinations. This process does not always work, but it seems to hold true in many cases. After you have factored the first and last terms and are beginning to look for the proper combinations, start with the intermediate factors and not the extreme ones.
Sample Set B
Factor \(24x^2 - 41x + 12\)
Factor the first and last terms.
| \(24x^2\) | \(12\) |
| \(24x, x\) | \(-12, -1\) |
| \(12x, 2x\) | \(-12, -1\) |
| \(8x, 3x\) | \(-6, -2\) |
| \(6x, 4x\) |
Rather than starting with the \(24x, x\) and \(-12, -1\), pick some intermediate values, \(8x\) and \(3x\), the \(6x\) and \(4x\), or the \(-6\) and \(-2\), or the \(-4\) and \(-3\).
\(24x^2 - 41x + 12 = (8x-3)(3x-4)\)
Practice Set B
Factor \(48x^2+22x−15\).
- Answer
-
\((6x+5)(8x−3)\)
Factor \(54y^2+39yw−28w^2\).
- Answer
-
\((9y−4w)(6y+7w)\)
The Collect and Discard Method of Factoring \(ax^2+bx+c\)
Collect and Discard Method
Consider the polynomial \(6x^2+x−12\). We begin by identifying \(a\) and \(c\). In this case, \(a=6\) and \(c=−12\). We start out as we would with \(a=1\).
\(6x^2+x−12: (6x)(6x)\)
Now, compute \(a \cdot c\).
\(a \cdot c=(6)(−12)=−72\)
Find the factors of \(−72\) that add to \(1\), the coefficient of \(x\), the linear term. The factors are \(9\) and \(−8\). Include these factors in the parentheses.
\(6x^2+x−12: (6x+9)(6x−8)\)
But we have included too much. We must eliminate the surplus. Factor each parenthesis.
\(6x^2+x−12: 3(2x+3) \cdot 2(3x−4)\)
Discard the factors that multiply to \(a=6\). In this case, \(3\) and \(2\). We are left with the proper factorization.
\(6x^2+x−12=(2x+3)(3x−4)\)
Sample Set C
Factor \(10x^2+23x−5\).
Identify \(a=10\) and \(b=−5\).
\(10x^2+23x−5; (10x)(10x)\)
Compute
\(a \cdot c=(10)(−5)=−50\)
Find the factors of \(−50\) that add to \(+23\), the coefficient of \(x\), the linear term. The factors are \(25\) and \(−2\). Place these numbers into the parentheses.
\(10x^2+23x−5: (10x+25)(10x−2)\)
We have collected too much. Factor each set of parentheses and eliminate the surplus.
\(10x^2+23x−5: (5)(2x+5)⋅(2)(5x−1)\)
Discard the factors that multiply to \(a=10\). In this case, \(5\) and \(2\).
\(10x^2+23x−5=(2x+5)(5x−1)\)
Factor \(8x^2−30x−27\).
Identify \(a=8\) and \(c=−27\).
\(8x^2−30x−27: (8x)(8x)\)
Compute
\(a \cdot c=(8)(−27)=−216\)
Find the factors of \(−216\) that add to \(−30\), the coefficient of \(x\), the linear term. This requires some thought. The factors are \(−36\) and \(6\). Place these numbers into the parentheses.
\(8x^2−30x−27: (8x−36)(8x+6)\)
We have collected too much. Factor each set of parentheses and eliminate the surplus.
\(8x^2−30x−27: (4)(2x−9)⋅(2)(4x+3)\)
Discard the factors that multiply to \(a=8\). In this case, \(4\) and \(2\).
\(8x^2−30x−27=(2x−9)(4x+3)\)
Factor \(18x^2−5xy−2y^2\).
Identify \(a=18\) and \(c=−2\).
\(18x^2−5xy−2y^2: (18x)(18x)\)
Compute
\(a \cdot c=(18)(−2)=−36\)
Find the factors of \(−36\) that add to \(−5\), the coefficient of \(xy\). In this case, \(−9\) and \(4\). Place these numbers into the parentheses, affixing \(y\) to each.
\(18x^2−5xy−2y^2: (18x−9y)(18x+4y)\)
We have collected too much. Factor each set of parentheses and eliminate the surplus.
\(18x^2−5xy−2y^2: (9)(2x−y) \cdot (2)(9x+2y)\)
Discard the factors that multiply to \(a=18\). In this case, \(9\) and \(4\).
\(18x^2−5xy−2y^2=(2x−y)(9x+2y)\)
Practice Set C
Factor \(6x^2+7x−3\).
- Answer
-
\((3x−1)(2x+3)\)
Factor \(14x^2−31x−10\).
- Answer
-
\((7x+2)(2x−5)\)
Factor \(48x^2+22x−15\).
- Answer
-
\((6x+5)(8x−3)\)
Factor \(10x^2−23xw+12w^2\).
- Answer
-
\((5x−4w)(2x−3w)\)
Exercises
Factor the following problems, if possible.
\(x^2+3x+2\)
- Answer
-
\((x+2)(x+1)\)
\(x^2+7x+12\)
\(2x^2+7x+5\)
- Answer
-
\((2x+5)(x+1)\)
\(3x^2+4x+1\)
\(2x^2+11x+12\)
- Answer
-
\((2x+3)(x+4)\)
\(10x^2+33x+20\)
\(3x^2−x−4\)
- Answer
-
\((3x−4)(x+1)\)
\(3x^2+x−4\)
\(4x^2+8x−21\)
- Answer
-
\((2x−3)(2x+7)\)
\(2a^2−a−3\)
\(9a^2−7a+2\)
- Answer
-
not factorable
\(16a^2+16a+3\)
\(16y^2−26y+3\)
- Answer
-
\((8y−1)(2y−3)\)
\(3y^2+14y−5\)
\(10x^2+29x+10\)
- Answer
-
\((5x+2)(2x+5)\)
\(14y^2+29y−15\)
\(81a^2+19a+2\)
- Answer
-
not factorable
\(24x^2+34x+5\)
\(24x^2−34x+5\)
- Answer
-
\((6x−1)(4x−5)\)
\(24x^2−26x−5\)
\(24x^2+26x−5\)
- Answer
-
\((6x−1)(4x+5)\)
\(6a^2+13a+6\)
\(6x^2+5xy+y2\)
- Answer
-
\((3x+y)(2x+y)\)
\(6a^2−ay−y^2\)
For the following problems, the given trinomial occurs when solving the corresponding applied problem. Factor each trinomial. You do not need to solve the problem.
\(5r^2−24r−5\)
It takes 5 hours to paddle a boat 12 miles downstream and then back. The current flows at the rate of 1 mile per hour. At what rate was the boat paddled?
- Answer
-
\((5r+1)(r−5)\)
\(x^2+5x−84\)
The length of a rectangle is 5 inches more than the width of the rectangle. If the area of the rectangle is 84 square inches, what are the length and width of the rectangle?
\(x^2+24x−145\)
A square measures 12 inches on each side. Another square is to be drawn around this square in such a way that the total area is 289 square inches. What is the distance from the edge of the smaller square to the edge of the larger square? (The two squares have the same center.)
- Answer
-
\((x+29)(x−5)\)
\(x^2+8x−20\)
A woman wishes to construct a rectangular box that is open at the top. She wishes it to be 4 inches high and have a rectangular base whose length is three times the width. The material used for the base costs $2 per square inch, and the material used for the sides costs $1.50 per square inch. The woman will spend exactly $120 for materials. Find the dimension of the box (length of the base, width of the base, and height).
For the following problems, factor the trinomials if possible.
\(16x^2−8xy−3y^2\)
- Answer
-
\((4x+y)(4x−3y)\)
\(6a^2+7ab+2b^2\)
\(12a^2+7ab+12b^2\)
- Answer
-
not factorable
\(9x^2+18xy+8y^2\)
\(8a^2+10ab−6b^2\)
- Answer
-
\(2(4a^2+5ab−3b^2)\)
\(12a^2+54a−90\)
\(12b^4+30b^2a+12a^2\)
- Answer
-
\(6(2b^2+a)(b^2+2a)\)
\(30a^4b^4−3a^2b^2−6c^2\)
\(3a^6−3a^3b^2−18b^4\)
- Answer
-
\(3(a^3+2b^2)(a^3−3b^2)\)
\(20a^2b^2+2abc^2−6a^2c^4\)
\(14a^2z^2−40a^3z^2−46a^4z^2r\)
- Answer
-
\(2a^2z^2(7−20a−23a^2) \text{ or} −2a^2z^2(23a^2+20a−7)\)
Exercises for Review
Simplify \((a^3b^6)^4\)
Find the product \(x^2(x-3)(x+4)\)
- Answer
-
\(x^4+x^3−12x^2\)
Find the product \((5m-3n)^2\)
Solve the equation \(5(2x−1)−4(x+7)=0\).
- Answer
-
\(x = \dfrac{11}{2}\)
Factor \(x^5 - 8x^4 + 7x^3\)


