7.6: Graphing Equations in Slope-Intercept Form

Last updated
Save as PDF

Page ID: 49385

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Using the Slope and Intercept to Graph a Line

When a linear equation is given in the general form, $ax+by=c$, we observed that an efficient graphical approach was the intercept method. We let $x=0$ and computed the corresponding value of $y$, then let $y=0$ and computed the corresponding value of $x$.

When an equation is written in the slope-intercept form, $y=mx+b$, there are also efficient ways of constructing the graph. One way, but less efficient, is to choose two or three $x$-values and compute to find the corresponding $y$-values. However, computations are tedious, time consuming, and can lead to errors. Another way, the method listed below, makes use of the slope and the $y$-intercept for graphing the line. It is quick, simple, and involves no computations.

Graphing Method

Plot the $y$-intercept $(0, b)$.
Determine another point by using the slope m.
Draw a line through the two points.

Recall that we defined the slope $m$ as the ratio $\dfrac{y_2-y_1}{x_2-x_1}$. The numerator $y_2−y_1$ represents the number of units that $y$ changes and the denominator $x_2 - x_1$ represents the number of units that $x$ changes. Suppose $m=pq$. Then $p$ is the number of units that $y$ changes and $q$ is the number of units that $x$ changes. Since these changes occur simultaneously, start with your pencil at the $y$-intercept, move $p$ units in the appropriate vertical direction, and then move $q$ units in the appropriate horizontal direction. Mark a point at this location.

Sample Set A

Graph the following lines.

Example $\PageIndex{1}$

$y = \dfrac{3}{4}x + 2$

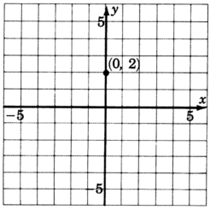
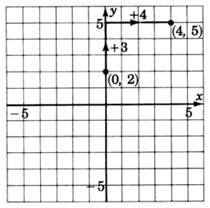
1. The $y$-intercept is the point $(0,2)$. Thus the line crosses the $y$-axis $2$ units above the origin. Mark a point at $(0,2)$.

$An xy coordinate plane with gridlines from negative five to five in increments of one unit for both axes. The point zero, two is plotted and labeled on the grid.$

2. The slope, $m$, is $\dfrac{3}{4}$. This means that if we start at any point on the line and move our pencil $3$ units up and then $4$ units to the right, we’ll be back on the line. Start at a known point, the $y$-intercept $(0, 2)$. Move up $3$ units, then move $4$ units to the right. Mark a point at this location. (Note also that \dfrac{3}{4} = \dfrac{-3}{-4}\). This means that if we start at any point on the line and move our pencil $3$ units down and $4$ units to the left, we’ll be back on the line. Note also that $\dfrac{3}{4} = \dfrac{\dfrac{3}{4}}{1}$. This means that if we start at any point on the line and move to the right $1$ unit, we’ll have to move up $\dfrac{3}{4}$ unit to get back on the line.)

$Starting at point with coordinates zero, two move three units up and four units right to reach to the point with coordinates four, five.$

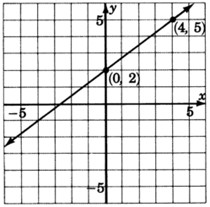
3. Draw a line through both points.

$A graph of a line passing through two points with coordinates zero, two, and four, five.$

Example $\PageIndex{2}$

$y = -\dfrac{1}{2}x + \dfrac{7}{2}$

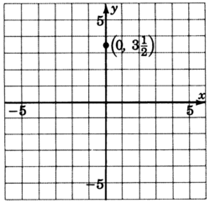
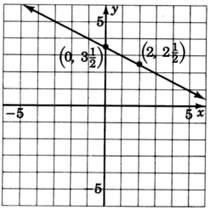
1. The $y$-intercept is the point $(0, \dfrac{7}{2})$. Thus the line crosses the $y$-axis $\dfrac{7}{2}$ units above the origin. Mark a point $(0, \dfrac{7}{2})$, or $(0, 3\dfrac{1}{2})$.

$An xy coordinate plane with gridlines from negative five to five and increments of one unit for both axes. The point zero, three and one half is plotted and labeled.$

2. The slope, $m$, is $-\dfrac{1}{2}$. We can write $-\dfrac{1}{2}$ as $\dfrac{-1}{2}$. Thus, we start at a known point, the $y$-intercept $(0, 3\dfrac{1}{2})$, move down one unit (because of the $-1$), then move right $2$ units. Mark a point at this location.

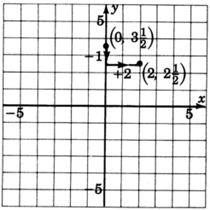
$Starting at point with coordinates zero, three and half move one unit downward and two units right to reach to the point with coordinates two, two and half.$

3. Draw a line through both points.

$A graph of a line passing through two points with coordinates zero, three and one half; and two, two and one half.$

Example $\PageIndex{3}$

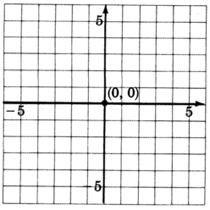
$y = \dfrac{2}{5}x$

1. We can put this equation into explicit slope-intercept by writing it as $y = \dfrac{2}{5}x + 0$.

The $y$-intercept is at the point $(0, 0)$, the origin. This line goes right through the origin.

$An xy coordinate plane with gridlines from negative five to five and increments of one unit for both axes. The origin is labeled with the coordinate pair zero, zero.$

2. The slope, $m$, is $\dfrac{2}{5}$. Starting at the origin, we move up $2$ units, then move to the right $5$ units. Mark a point at this location.

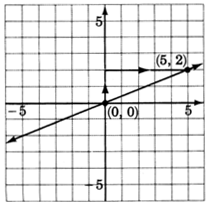
$A graph of a line passing through two points with coordinates zero, zero; and five, two. Starting at a point with coordinates zero, zero moves two units up and five units to the right to reach to the point with coordinates five, two.$

3. Draw a line through the two points.

Example $\PageIndex{4}$

$y = 2x - 4$

1. The $y$-intercept is the point $(0, -4)$. Thus the line crosses the $y$-axis $4$ units below the origin. Mark a point at $(0, -4)$.

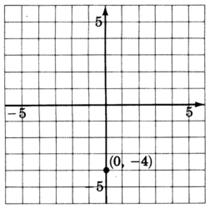
$A point with the coordinates zero, negative four plotted in an xy plane.$

2. The slope, $m$, is $2$. If we write the slope as a fraction, $2 = \dfrac{2}{1}$, we can read how to make the changes. Start at the known point $(0, -4)$, move up $2$ units, then move right $1$ unit. Mark a point at this location.

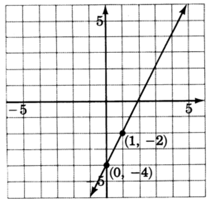
$A graph of a line passing through two points with coordinates zero, negative four and one, negative two.$

3. Draw a line through the two points.

Practice Set A

Use the $y$-intercept and the slope to graph each line.

Practice Problem $\PageIndex{1}$

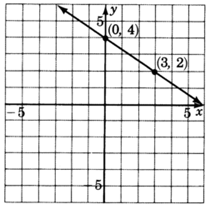
$y = \dfrac{-2}{3} + 4$

$An xy-plane with gridlines, labeled negative five and five and increments of one unit for both axes.$

Answer: $A graph of a line passing through two points with coordinates zero, four and three, two.$

Practice Problem $\PageIndex{2}$

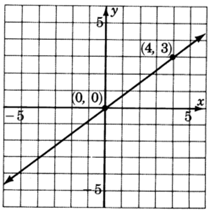
$y = \dfrac{3}{4}x$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Answer: $A graph of a line passing through two points with coordinates zero, zero and four, three.$

Exercises

For the following problems, graph the equations.

Exercise $\PageIndex{1}$

$y = \dfrac{2}{3} + 1$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

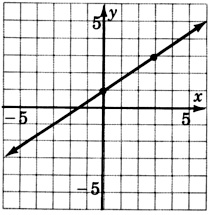
Answer: $A graph of a line passing through two points with coordinates zero, one and three, three.$

Exercise $\PageIndex{2}$

$y = \dfrac{1}{4}x - 2$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{3}$

$y = 5x - 4$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

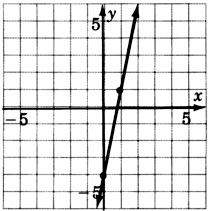
Answer: $A graph of a line passing through two points with coordinates zero, negative four and one, one.$

Exercise $\PageIndex{4}$

$y = -\dfrac{6}{5} - 3$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{5}$

$y = \dfrac{3}{2} - 5$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

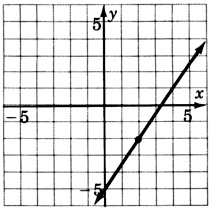
Answer: $A graph of a line passing through two points with coordinates zero, negative five and two, negative two.$

Exercise $\PageIndex{6}$

$y = \dfrac{1}{5}x + 2$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{7}$

$y = -\dfrac{8}{3} + 4$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

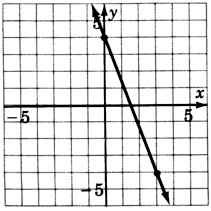
Answer: $A graph of a line passing through two points with coordinates zero, four and three, negative four.$

Exercise $\PageIndex{8}$

$y = -\dfrac{10}{3} + 6$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{9}$

$y = 1x - 4$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

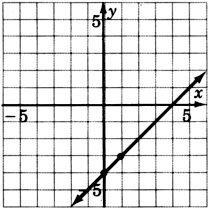
Answer: $A graph of a line passing through two points with coordinates zero, negative four and one, negative three.$

Exercise $\PageIndex{10}$

$y = -2x + 1$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{11}$

$y = x + 2$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

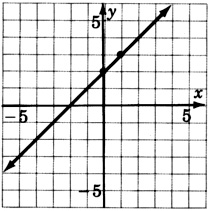
Answer: $A graph of a line passing through two points with coordinates zero, two and one, three.$

Exercise $\PageIndex{12}$

$y = \dfrac{3}{5}x$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{13}$

$y = -\dfrac{4}{3}$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

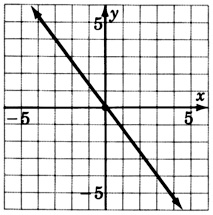
Answer: $A graph of a line passing through two points with coordinates zero, zero and negative three, four.$

Exercise $\PageIndex{14}$

$y = x$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{15}$

$y = -x$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

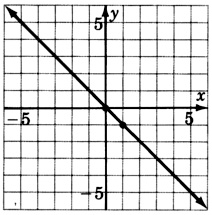
Answer: $A graph of a line passing through two points with coordinates zero, zero and one, negative one.$

Exercise $\PageIndex{16}$

$3y−2x=−3$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercise $\PageIndex{17}$

$6x+10y=30$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

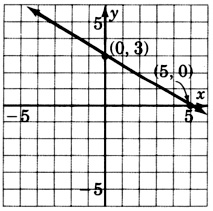
Answer: $A graph of a line passing through two points with coordinates zero, three and five, zero.$

Exercise $\PageIndex{18}$

$x+y=0$

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Exercises for Review

Exercise $\PageIndex{19}$

Solve the inequality $2 - 4x \ge x - 3$

Answer: $x≤1$

Exercise $\PageIndex{20}$

Graph the inequality $y+3>1.$

$A horizontal line with arrows on both ends.$

Exercise $\PageIndex{21}$

Graph the equation $y = -2$.

$An xy-plane with gridlines, labeled negative five and five on the both axes.$

Answer: $A graph of a line parallel to x-axis in an xy plane.The line crosses the y-axis at y equals negative two.$

Exercise $\PageIndex{22}$

Determine the slope and $y$-intercept of the line $−4y−3x=16$.

Exercise $\PageIndex{23}$

Find the slope of the line passing through the points $(−1, 5)$ and $(2, 3)$.

Answer: $m = \dfrac{-2}{3}$

Search

Graphing Method

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Practice Problem \(\PageIndex{1}\)

Practice Problem \(\PageIndex{2}\)

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)