9.2: Square Root Expressions
- Page ID
- 49394
Square Roots
When we studied exponents in Section 2.5, we noted that \(4^2 = 16\) and \((-4)^2 = 16\). We can see that \(16\) is a square of both \(4\) and \(-4\). Since \(16\) comes from squaring \(4\) or \(-4\), \(4\) and \(-4\) are called the square roots of \(16\). Thus, \(16\) has two square roots, \(4\) and \(-4\). Notice that these two square roots are opposites of each other.
We can say that
The square root of a positive number \(x\) is a number such that when it is squared the number \(x\) results.
Every positive number has two square roots, one positive square root and one negative square root. Furthermore, the two square roots of a positive number are opposites of each other. The square root of 0 is 0.
Sample Set A
The two square roots of \(49\) are \(7\) and \(-7\) since:
\(7^2 = 49\) and \((-7)^2 = 49\).
The two square roots of \(\dfrac{49}{64}\) are \(\dfrac{7}{8}\) and \(\dfrac{-7}{8}\) since:
\((\dfrac{7}{8})^2 = \dfrac{7}{8} \cdot \dfrac{7}{8} = \dfrac{49}{64}\) and \((\dfrac{-7}{8})^2 = \dfrac{-7}{8} \cdot \dfrac{-7}{8} = \dfrac{49}{64}\)
Practice Set A
Name both square roots of each of the following numbers.
\(36\)
- Answer
-
\(6\) and \(-6\)
\(25\)
- Answer
-
\(5\) and \(-5\).
\(100\)
- Answer
-
\(10\) and \(-10\)
\(64\)
- Answer
-
\(8\) and \(-8\)
\(1\)
- Answer
-
\(1\) and \(-1\)
\(\dfrac{1}{4}\)
- Answer
-
\(\dfrac{1}{2}\) and \(-\dfrac{1}{2}\)
\(\dfrac{9}{16}\)
- Answer
-
\(\dfrac{3}{4}\) and \(-\dfrac{3}{4}\)
\(0.1\)
- Answer
-
\(0.1\) and \(−0.1\)
\(0.09\)
- Answer
-
\(0.03\) and \(−0.03\)
Principal and Secondary Square Roots
There is a notation for distinguishing the positive square root of a number \(x\) from the negative square root of \(x\).
If \(x\) is a positive real number, then
\(\sqrt{x}\) represents the positive square root of \(x\). The positive square root of a number is called the principal square root of the number.
\(-\sqrt{x}\) represents the negative square root of \(x\). The negative square root of a number is called the secondary square root of the number.
\(-\sqrt{x}\) indicates the secondary square root of \(x\).
In the expression \(\sqrt{x}\),
\(\sqrt{}\) is called a radical sign.
\(x\) is called the radicand.
\(\sqrt{x}\) is called a radical
The horizontal bar that appears attached to the radical sign, \(\sqrt{}\), is a grouping symbol that specifies the radicand.
Because \(\sqrt{x}\) and \(-\sqrt{x}\) are the two square roots of \(x\),
\((\sqrt{x})(\sqrt{x}) = x\) and \((-\sqrt{x})(-\sqrt{x}) = x\).
Sample Set B
Write the principal and secondary square roots of each number.
\(9\)
Principal Square Root: \(\sqrt{9} = 3\)
Secondary Square Root: \(-\sqrt{9} = -3\)
\(15\)
Principal Square Root: \(\sqrt{15}\)
Secondary Square Root: \(-\sqrt{15}\)
Use a calculator to obtain a decimal approximation for the two square roots of \(34\). Round to two decimal places.
On the calculator:
Type: \(34\)
Press: \(\sqrt{}\)
Display Reads: \(5.8309519\)
Rount to \(5.83\)
Notice that the square root symbol on the calculator is \(\sqrt{}\). This means, of course, that a calculator will produce only the positive square root. We must supply the negative square root ourselves.
\(\sqrt{34}\) \approx 5.83\) and \(-\sqrt{34} \approx -5.83\)
Notice: the symbol \(\approx\) means "approximately equal to."
The number \(\sqrt{50}\) is between what two whole numbers?
Since \(7^2 = 49, \sqrt{49} = 7\).
Since \(8^2 = 64, \sqrt{64} = 8\). Thus,
\(7 < \sqrt{50} < 8\)
Thus, \(\sqrt{50}\) is a number between \(7\) and \(8\).

Practice Set B
Write the principal and secondary square roots of each number.
\(100\)
- Answer
-
\(\sqrt{100} = 10\) and \(-\sqrt{100} = -10\)
\(121\)
- Answer
-
\(\sqrt{121} = 11\) and \(-\sqrt{121} = -11\)
\(35\)
- Answer
-
\(\sqrt{35}\) and \(-\sqrt{35}\)
Use a calculator to obtain a decimal approximation for the two square roots of \(35\). Round to two decimal places.
- Answer
-
\95.92\) and \(-5.92\)
Meaningful Expressions
Since we know that the square of any real number is a positive number or zero, we can see that expressions such as\(\sqrt{-16}\) do not describe real numbers. There is no real number that can be squared that will produce \(-16\). For \(\sqrt{x}\) to be a real number, we must have \(x \ge 0\). In our study of algebra, we will assume that all variables and all expressions in radicands represent nonnegative numbers (numbers greater than or equal to zero).
Sample Set C
Write the proper restrictions that must be placed on the variable so that each expression represents a real number.
\(\sqrt{x-3}\) to be a real number, we must have:
\(x - 3 \ge 0\) or \(x \ge 3\)
For \(\sqrt{2m + 7}\) to be a real number, we must have:
\(2m + 7 \ge 0\) or \(2m \ge -7\) or \(m \ge \dfrac{-7}{2}\)
Practice Set C
Write the proper restrictions that must be placed on the variable so that each expression represents a real number.
\(\sqrt{x+5}\)
- Answer
-
\(x \ge -5\)
\(\sqrt{y - 8}\)
- Answer
-
\(y≥8\)
\(\sqrt{3a + 2}\)
- Answer
-
\(a \ge -\dfrac{2}{3}\)
\(\sqrt{5m - 6}\)
- Answer
-
\(m \ge \dfrac{6}{5}\)
Simplifying Square Roots
When variables occur in the radicand, we can often simplify the expression by removing the radical sign. We can do so by keeping in mind that the radicand is the square of some other expression. We can simplify a radical by seeking an expression whose square is the radicand. The following observations will help us find the square root of a variable quantity.
Since \((x^3)^2 = x^{3 \cdot 2} - x^6, x^3\) is a square root of \(x^6\). Also
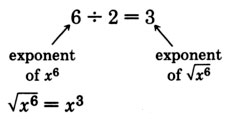
Since \((x^4)^2 = x^{4 \cdot 2} = x^8, x^4\) is a square root of \(x^8\). Also
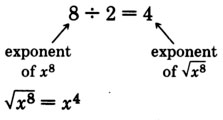
Since \((x^6)^2 = x^{6 \cdot 2} = x^{12}, x^6\) is a square root of \(x^{12}\). Also
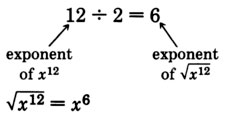
These examples suggest the following rule:
If a variable has an even exponent, its square root can be found by dividing that exponent by \(2\).
The examples of Sample Set B illustrate the use of this rule.
Sample Set D
Simplify each expression by removing the radical sign. Assume each variable is nonnegative.
\(\sqrt{a^2}\) We seek an expresssion whose square is \(a^2\). Since \((a)^2 = a^2\),
\(\sqrt{a^2} = a\) Notice that \(2 \div 2 = 1\)
\(\sqrt{y^8}\) We seek an expression whose square is \(y^8\). Since \((y^4)^2 = y^8\),
\(\sqrt{y^8} = y^4\) Notice that \(8 \div 2 = 4\).
\(\sqrt{25m^2n^6}\). We seek an expression whose square is \(25m^2n^6\). Since \((5mn^3)^2 = 25m^2n^6\),
\(\sqrt{25m^2n^6} = 5mn^3\) Notice that \(2 \div 2 = 1\) and \(6 \div 2 = 3\).
\(-\sqrt{121a^{10}(b-1)^4}\) We seek an expression whose square is \(121a^{10}(b-1)^4\). Since
\(\begin{array}{flushleft}
\left[11 a^{5}(b-1)^{2}\right]^{2} &= 121a^{10}(b-1)^4,\\
\sqrt{121a^{10}(b-1)^4} &= 1a^5(b-1)^2\\
\text{Then, } -\sqrt{121a^{10}(b-1)^4} &= -11a^5(b-1)^2 & \text{Notice that } 10 \div 2 = 5 \text{ and } 4 \div 2 = 2
\end{array}\)
Practice Set D
Simplify each expression by removing the radical sign. Assume each variable is nonnegative.
\(\sqrt{y^8}\)
- Answer
-
\(y^4\)
\(\sqrt{16a^4}\)
- Answer
-
\(4a^2\)
\(\sqrt{49x^4y^6}\)
- Answer
-
\(7x^2y^3\)
\(-\sqrt{100x^8y^{12}z^2}\)
- Answer
-
\(-10x^4y^6z\)
\(-\sqrt{36(a+5)^4}\)
- Answer
-
\(-6a(a+5)^2\)
\(\sqrt{225w^4(z^2-1)^2}\)
- Answer
-
\(15w^2(z^2 - 1)\)
\(\sqrt{0.25y^6z^{14}}\)
- Answer
-
\(0.5y^3z^7\)
\(\sqrt{x^{2n}}\), where \(n\) is a natural number
- Answer
-
\(x^n\)
\(\sqrt{x^{4n}}\), where \(n\) is a natural number.
- Answer
-
\(x^{2n}\)
Exercises
How many square roots does every positive real number have?
- Answer
-
two
The symbol \(\sqrt{}\) represents which square root of a number?
The symbol \(-\sqrt{}\) represents which square root of a number?
- Answer
-
secondary
For the following problems, find the two square roots of the given number.
64
81
- Answer
-
9 and −9
25
121
- Answer
-
11 and −11
144
225
- Answer
-
15 and −15
10,000
\(\dfrac{1}{16}\)
- Answer
-
\(\dfrac{1}{4}\) and \(-\dfrac{1}{4}\)
\(\dfrac{1}{49}\)
\(\dfrac{25}{36}\)
- Answer
-
\(\dfrac{5}{6}\) and \(-\dfrac{5}{6}\)
\(\dfrac{121}{225}\)
\(0.04\)
- Answer
-
\(0.2\) and \(-0.2\)
\(0.16\)
\(1.21\)
- Answer
-
\(1.1\) and \(−1.1\)
For the following problems, evaluate each expression. If the expression does not represent a real number, write "not a real number."
\(\sqrt{49}\)
\(\sqrt{64}\)
- Answer
-
\(8\)
\(-\sqrt{36}\)
\(-\sqrt{100}\)
- Answer
-
\(-10\)
\(-\sqrt{169}\)
\(-\sqrt{\dfrac{36}{81}}\)
- Answer
-
\(\dfrac{2}{3}\)
\(-\sqrt{\dfrac{121}{169}}\)
\(\sqrt{-225}\)
- Answer
-
not a real number
\(\sqrt{-36}\)
\(-\sqrt{-1}\)
- Answer
-
not a real number
\(-\sqrt{-5}\)
\(-(-\sqrt{9})\)
- Answer
-
\(3\)
\(-(-\sqrt{0.81})\)
For the following problems, write the proper restrictions that must be placed on the variable so that the expression represents a real number.
\(\sqrt{y + 10}\)
- Answer
-
\(y≥−10\)
\(\sqrt{x + 4}\)
\(\sqrt{a - 16}\)
- Answer
-
\(a≥16\)
\(\sqrt{h - 11}\)
\(\sqrt{2k - 1}\)
- Answer
-
\(k \ge \dfrac{1}{2}\)
\(\sqrt{7x + 8}\)
\(\sqrt{-2x - 8}\)
- Answer
-
\(x≤−4\)
\(\sqrt{-5y + 15}\)
For the following problems, simplify each expression by removing the radical sign.
\(\sqrt{m^6}\)
- Answer
-
\(m^3\)
\(\sqrt{k^{10}}\)
\(\sqrt{a^8}\)
- Answer
-
\(a^4\)
\(\sqrt{h^{16}}\)
\(\sqrt{x^4y^{10}}\)
- Answer
-
\(x^2y^5\)
\(\sqrt{a^6b^{20}}\)
\(\sqrt{a^4b^6}\)
- Answer
-
\(a^2b^3\)
\(\sqrt{x^8y^{14}}\)
\(\sqrt{81a^2b^2}\)
- Answer
-
\(9ab\)
\(\sqrt{49x^6y^4}\)
\(\sqrt{100m^8n^2}\)
- Answer
-
\(10m^4n\)
\(\sqrt{225p^{14}r^{16}}\)
\(\sqrt{36x^{22}y^{44}}\)
- Answer
-
\(6x^{11}y^{22}\)
\(\sqrt{169w^4z^6(m-1)^2}\)
\(\sqrt{25x^{12}(y-1)^4}\)
- Answer
-
\(5x^6(y-1)^2\)
\(\sqrt{64a^{10}(a+4)^{14}}\)
\(\sqrt{9m^6n^4(m + n)^{18}}\)
- Answer
-
\(3m^3n^2(m + n)^9\)
\(\sqrt{25m^{26}n^{42}r^{66}s^{84}}\)
\(\sqrt{(f-2)^2(g+6)^4}\)
- Answer
-
\((f-2)(g+6)^4\)
\(\sqrt{(2c - 3)^6 + (5c + 1)^2}\)
\(-\sqrt{64r^4s^{22}}\)
- Answer
-
\(-8r^2s^{11}\)
\(-\sqrt{121a^6(a-4)^8}\)
\(-[-\sqrt{(w+6)^2}]\)
- Answer
-
\(w + 6\)
\(-[-\sqrt{4a^2b^2(c^2 + 8)^2}]\)
\(\sqrt{1.21h^4k^4}\)
- Answer
-
\(1.1h^2k^2\)
\(\sqrt{2.25m^6p^6}\)
\(-\sqrt{\dfrac{169a^2b^4c^6}{196x^4y^6z^8}}\)
- Answer
-
\(-\dfrac{12ab^2c^3}{14x^2y^3z^4}\)
\(-[\sqrt{\dfrac{81y^4(z-1)^2}{225x^8z^4w^6}}]\)
Exercises for Review
Find the quotient. \(\dfrac{x^2 - 1}{4x^2 - 1} \div \dfrac{x-1}{2x + 1}\)
- Answer
-
\(\dfrac{x+1}{2x-1}\)
Find the sum. \(\dfrac{1}{x+1} + \dfrac{3}{x+1} + \dfrac{2}{x^2 - 1}\)
Solve the equation, if possible: \(\dfrac{1}{x-2} = \dfrac{3}{x^2 - x - 2} - \dfrac{3}{x+1}\)
- Answer
-
No solution; \(x=2\) is excluded.
Perform the division: \(\dfrac{15x^3 - 5x^2 + 10x}{5x}\)
Perform the division: \(\dfrac{x^3 - 5x^2 + 13x - 21}{x-3}\)
- Answer
-
\(x^2 - 2x + 7\)


