9.5: Division of Square Root Expressions
- Page ID
- 49397
The Division Property of Square Roots
In our work with simplifying square root expressions, we noted that
\[\sqrt{\dfrac{x}{y}} = \dfrac{\sqrt{x}}{\sqrt{y}} \nonumber\]
Since this is an equation, we may write it as:
\[\dfrac{\sqrt{x}}{\sqrt{y}} = \sqrt{\dfrac{x}{y}} \nonumber\]
To divide two square root expressions, we use the division property of square roots:
\[\dfrac{\sqrt{x}}{\sqrt{y}} = \sqrt{\dfrac{x}{y}}\]
The quotient of the square root is the square root of the quotient.
Rationalizing the Denominator
As we can see by observing the right side of the equation governing the division of square roots, the process may produce a fraction in the radicand. This means, of course, that the square root expression is not in simplified form. It is sometimes more useful to rationalize the denominator of a square root expression before actually performing the division.
Sample Set A
Simplify the square root expressions.
\[\sqrt{\dfrac{3}{7}} \nonumber\]
This radical expression is not in simplified form since there is a fraction under the radical sign. We can eliminate this problem using the division property of square roots.
\[\sqrt{\dfrac{3}{7}} = \dfrac{\sqrt{3}}{\sqrt{7}} = \dfrac{\sqrt{3}}{\sqrt{7}} \cdot \dfrac{\sqrt{7}}{\sqrt{7}} = \dfrac{\sqrt{3} \sqrt{7}}{7} = \dfrac{\sqrt{21}}{7} \nonumber\]
\(\dfrac{\sqrt{5}}{\sqrt{3}}\)
A direct application of the rule produces \(\sqrt{\dfrac{5}{3}}\), which must be simplified. Let us rationalize the denominator before we perform the division.
\(\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{5}}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{\sqrt{5} \sqrt{3}}{3}=\dfrac{\sqrt{15}}{3}\)
\(\dfrac{\sqrt{21}}{\sqrt{7}} = \sqrt{\dfrac{21}{7}} = \sqrt{3}\)
The rule produces the quotient quickly. We could also rationalize the denominator first and produce the same result.
\(\dfrac{\sqrt{21}}{\sqrt{7}}=\dfrac{\sqrt{21}}{7} \cdot \dfrac{\sqrt{7}}{\sqrt{7}}=\dfrac{\sqrt{21 \cdot 7}}{7}=\dfrac{\sqrt{3 \cdot 7 \cdot 7}}{7}=\dfrac{\sqrt{3 \cdot 7^{2}}}{7}=\dfrac{7 \sqrt{3}}{7}=\sqrt{3}\)
\(\dfrac{\sqrt{80 x^{9}}}{\sqrt{5 x^{4}}}=\sqrt{\dfrac{80 x^{9}}{5 x^{4}}}=\sqrt{16 x^{5}}=\sqrt{16} \sqrt{x^{4} x}=4 x^{2} \sqrt{x}\)
\(\dfrac{\sqrt{50 a^{3} b^{7}}}{\sqrt{5 a b^{5}}}=\sqrt{\dfrac{50 a^{3} b^{7}}{5 a b^{5}}}=\sqrt{10 a^{2} b^{2}}=a b \sqrt{10}\)
\(\dfrac{\sqrt{5a}}{\sqrt{b}}\)
Some observation shows that a direct division of the radicands will produce a fraction. This suggests that we rationalize the denominator first.
\(\dfrac{\sqrt{5a}}{\sqrt{b}} = \dfrac{\sqrt{5a}}{\sqrt{b}} \cdot \dfrac{\sqrt{b}}{\sqrt{b}} = \dfrac{\sqrt{5a} \sqrt{b}}{b} = \dfrac{\sqrt{5ab}}{b}\)
\(\dfrac{\sqrt{m-6}}{\sqrt{m+2}} = \dfrac{\sqrt{m-6}}{\sqrt{m+2}} \cdot \dfrac{\sqrt{m+2}}{\sqrt{m+2}} = \dfrac{\sqrt{m^2 - 4m - 12}}{m + 2}\)
\(\dfrac{\sqrt{y^{2}-y-12}}{\sqrt{y+3}}=\sqrt{\dfrac{y^{2}-y-12}{y+3}}=\sqrt{\dfrac{(y+3)(y-4)}{(y+3)}}=\sqrt{\dfrac{\cancel{(y+3)}(y-4)}{\cancel{(y+3)}}}=\sqrt{y-4}\)
Practice Set A
Simplify the square root expressions.
\(\dfrac{\sqrt{26}}{\sqrt{13}}\)
- Answer
-
\(\sqrt{2}\)
\(\dfrac{\sqrt{7}}{\sqrt{3}}\)
- Answer
-
\(\dfrac{\sqrt{21}}{3}\)
\(\dfrac{\sqrt{80m^5n^8}}{\sqrt{5m^2n}}\)
- Answer
-
\(4mn^3 \sqrt{mn}\)
\(\dfrac{\sqrt{196(x+7)^8}}{\sqrt{2(x+7)^3}}\)
- Answer
-
\(7(x+7)^2 \sqrt{2(x+7)}\)
\(\dfrac{\sqrt{n+4}}{\sqrt{n-5}}\)
- Answer
-
\(\dfrac{\sqrt{n^2 - n - 20}}{n-5}\)
\(\dfrac{\sqrt{a^2 - 6a + 8}}{\sqrt{a-2}}\)
- Answer
-
\(\sqrt{a-4}\)
\(\dfrac{\sqrt{x^{2n}}}{\sqrt{x^n}}\)
- Answer
-
\(x^n\)
\(\dfrac{\sqrt{a^{3m-5}}}{\sqrt{a^{m-1}}}\)
- Answer
-
\(a^{m-2}\)
Conjugates and Rationalizing the Denominator
To perform a division that contains a binomial in the denominator, such as \(\dfrac{3}{4 + \sqrt{6}}\), we multiply the numerator and denominator by a conjugate of the denominator.
A conjugate of the binomial \(a + b\) is \(a-b\). Similarly, a conjugate of \(a-b\) is \(a + b\).
Notice that when the conjugates \(a + b\) and \(a - b\) are multiplied together, they produce a difference of two squares.
\((a+b)(a-b) = a^2 - ab + ab - b^2 = a^2 - b^2\)
This principle helps us eliminate square root radicals, as shown in these examples that illustrate the produce of conjugates.
\(\begin{array}{flushleft}
(5 + \sqrt{2})(5 - \sqrt{2}) &= 5^2 - (\sqrt{2})^2\\
&= 25 - 2\\
&= 23
\end{array}\)
\(\begin{array}{flushleft}
(\sqrt{6} - \sqrt{7})(\sqrt{6} + \sqrt{7}) &= (\sqrt{6})^2 - (\sqrt{7})^2\\
&= 6 - 7\\
&= -1
\end{array}\)
Sample Set B
Simplify the following expressions.
\(\dfrac{3}{4 + \sqrt{6}}\)
The conjugate of the denominator is \(4 - \sqrt{6}\). Multiply the fraction by \(1\) in the form of \(\dfrac{4 - \sqrt{6}}{4 - \sqrt{6}}\)
\(\begin{array}{flushleft}
\dfrac{3}{4 + \sqrt{6}} \cdot \dfrac{4 - \sqrt{6}}{4 - \sqrt{6}} &= \dfrac{3(4 - \sqrt{6})}{4^2 - (\sqrt{6})^2}\\
&= \dfrac{12 - 3\sqrt{6}}{16 - 6}\\
&= \dfrac{12 - 3\sqrt{6}}{10}
\end{array}\)
\(\dfrac{\sqrt{2x}}{\sqrt{3} - \sqrt{5x}}\)
The conjugate of the denominator is \(\sqrt{3} + \sqrt{5x}\). Multiply the fraction by \(1\) in the form of \(\dfrac{\sqrt{3} + \sqrt{5x}}{\sqrt{3} + \sqrt{5x}}\).
\(\begin{array}{flushleft}
\dfrac{\sqrt{2 x}}{\sqrt{3}-\sqrt{5 x}} \cdot \dfrac{\sqrt{3}+\sqrt{5 x}}{\sqrt{3}+\sqrt{5 x}} &=\dfrac{\sqrt{2 x}(\sqrt{3}+\sqrt{5 x})}{(\sqrt{3})^{2}-(\sqrt{5 x})^{2}} \\
&=\dfrac{\sqrt{2 x} \sqrt{3}+\sqrt{2 x} \sqrt{5 x}}{3-5 x} \\
&=\dfrac{\sqrt{6 x}+\sqrt{10 x^{2}}}{3-5 x} \\
&=\dfrac{\sqrt{6 x}+x \sqrt{10}}{3-5 x}
\end{array}\)
Practice Set B
Simplify the following expressions.
\(\dfrac{5}{9 + \sqrt{7}}\)
- Answer
-
\(\dfrac{45 - 5\sqrt{7}}{74}\)
\(\dfrac{-2}{1 - \sqrt{3x}}\)
- Answer
-
\(\dfrac{-2 - 2\sqrt{3x}}{1 - 3x}\)
\(\dfrac{\sqrt{8}}{\sqrt{3x} + \sqrt{2x}}\)
- Answer
-
\(\dfrac{2\sqrt{6x} - 4\sqrt{x}}{x}\)
\(\dfrac{\sqrt{2m}}{m - \sqrt{3m}}\)
- Answer
-
\(\dfrac{\sqrt{2m} + \sqrt{6}}{m - 3}\)
Exercises
For the following problems, simplify each expression.
\(\dfrac{\sqrt{28}}{\sqrt{2}}\)
- Answer
-
\(\sqrt{14}\)
\(\dfrac{\sqrt{200}}{\sqrt{10}}\)
\(\dfrac{\sqrt{28}}{\sqrt{7}}\)
- Answer
-
\(2\)
\(\dfrac{\sqrt{96}}{\sqrt{24}}\)
\(\dfrac{\sqrt{180}}{\sqrt{5}}\)
- Answer
-
\(6\)
\(\dfrac{\sqrt{336}}{\sqrt{21}}\)
\(\dfrac{\sqrt{162}}{\sqrt{18}}\)
- Answer
-
\(3\)
\(\sqrt{\dfrac{25}{9}}\)
\(\sqrt{\dfrac{36}{35}}\)
- Answer
-
\(\dfrac{6\sqrt{35}}{35}\)
\(\sqrt{\dfrac{225}{16}}\)
\(\sqrt{\dfrac{49}{225}}\)
- Answer
-
\(\dfrac{7}{15}\)
\(\sqrt{\dfrac{3}{5}}\)
\(\sqrt{\dfrac{3}{7}}\)
- Answer
-
\(\dfrac{\sqrt{21}}{7}\)
\(\sqrt{\dfrac{1}{2}}\)
\(\sqrt{\dfrac{5}{2}}\)
- Answer
-
\(\dfrac{\sqrt{10}}{2}\)
\(\sqrt{\dfrac{11}{25}}\)
\(\sqrt{\dfrac{15}{36}}\)
- Answer
-
\(\dfrac{\sqrt{15}}{6}\)
\(\sqrt{\dfrac{5}{16}}\)
\(\sqrt{\dfrac{7}{25}}\)
- Answer
-
\(\dfrac{\sqrt{7}}{5}\)
\(\sqrt{\dfrac{32}{49}}\)
\(\sqrt{\dfrac{50}{81}}\)
- Answer
-
\(\dfrac{5 \sqrt{2}}{9}\)
\(\dfrac{\sqrt{125x^5}}{\sqrt{5x^3}}\)
\(\dfrac{\sqrt{72m^7}}{\sqrt{2m^3}}\)
- Answer
-
\(6m^2\)
\(\dfrac{\sqrt{162a^{11}}}{\sqrt{2a^5}}\)
\(\dfrac{\sqrt{75y^{10}}}{\sqrt{2a^5}}\)
- Answer
-
\(5y^3\)
\(\dfrac{\sqrt{48x^9}}{\sqrt{3x^2}}\)
\(\dfrac{\sqrt{125a^{14}}}{\sqrt{5a^5}}\)
- Answer
-
\(5a^4 \sqrt{a}\)
\(\dfrac{\sqrt{27a^{10}}}{\sqrt{3a^5}}\)
\(\dfrac{\sqrt{108x^{21}}}{\sqrt{3x^4}}\)
- Answer
-
\(6x^8 \sqrt{x}\)
\(\dfrac{\sqrt{48x^6y^7}}{\sqrt{3xy}}\)
\(\dfrac{\sqrt{45a^3b^8c^2}}{\sqrt{5ab^2c}}\)
- Answer
-
\(3ab^3 \sqrt{c}\)
\(\dfrac{\sqrt{66m^{12}n^{15}}}{\sqrt{11mn^8}}\)
\(\dfrac{\sqrt{30p^5q^{14}}}{\sqrt{5q^7}}\)
- Answer
-
\(p^2q^3 \sqrt{6pq}\)
\(\dfrac{\sqrt{b}}{\sqrt{5}}\)
\(\dfrac{\sqrt{5x}}{\sqrt{2}}\)
- Answer
-
\(\dfrac{\sqrt{10x}}{2}\)
\(\dfrac{\sqrt{2a^3b}}{\sqrt{14a}}\)
\(\dfrac{\sqrt{3m^4n^3}}{\sqrt{6mn^5}}\)
- Answer
-
\(\dfrac{m \sqrt{2m}}{2n}\)
\(\dfrac{\sqrt{5(p-q)^6(r+s)^4}}{\sqrt{25(r+s)^3}}\)
\(\dfrac{\sqrt{m(m-6)-m^2 + 6m}}{\sqrt{3m - 7}}\)
- Answer
-
\(0\)
\(\dfrac{\sqrt{r+1}}{\sqrt{r-1}}\)
\(\dfrac{\sqrt{s+3}}{\sqrt{s-3}}\)
- Answer
-
\(\dfrac{\sqrt{s^2-9}}{s-3}\)
\(\dfrac{\sqrt{a^2 + 3a + 2}}{\sqrt{a + 1}}\)
\(\dfrac{\sqrt{x^2 - 10x + 24}}{\sqrt{x-4}}\)
- Answer
-
\(\sqrt{x-6}\)
\(\dfrac{\sqrt{x^2 - 2x - 8}}{\sqrt{x + 2}}\)
\(\dfrac{\sqrt{x^2 - 4x + 3}}{\sqrt{x-3}}\)
- Answer
-
\(\sqrt{x-1}\)
\(\dfrac{\sqrt{2x^2 - x - 1}}{\sqrt{x - 1}}\)
\(\dfrac{-5}{4 + \sqrt{5}}\)
- Answer
-
\(\dfrac{-20 + 5\sqrt{5}}{11}\)
\(\dfrac{1}{1 + \sqrt{x}}\)
\(\dfrac{2}{1 - \sqrt{a}}\)
- Answer
-
\(\dfrac{2(1 + \sqrt{a})}{1 - a}\)
\(\dfrac{-6}{\sqrt{5} - 1}\)
\(\dfrac{-6}{\sqrt{7} + 2}\)
- Answer
-
\(-2(\sqrt{7} - 2)\)
\(\dfrac{3}{\sqrt{3} - \sqrt{2}}\)
\(\dfrac{4}{\sqrt{6} + \sqrt{2}}\)
- Answer
-
\(\sqrt{6} - \sqrt{2}\)
\(\dfrac{\sqrt{5}}{\sqrt{8} - \sqrt{6}}\)
\(\dfrac{\sqrt{12}}{\sqrt{12} - \sqrt{8}}\)
- Answer
-
\(3 + \sqrt{6}\)
\(\dfrac{\sqrt{7x}}{2 - \sqrt{5x}}\)
\(\dfrac{\sqrt{6y}}{1 + \sqrt{3y}}\)
- Answer
-
\(\dfrac{\sqrt{6y} - 3y\sqrt{2}}{1 - 3y}\)
\(\dfrac{\sqrt{2}}{\sqrt{3} - \sqrt{2}}\)
\(\dfrac{\sqrt{a}}{\sqrt{a} + \sqrt{b}}\)
- Answer
-
\(\dfrac{a - \sqrt{ab}}{a - b}\)
\(\dfrac{\sqrt{8^3b^5}}{4 - \sqrt{2ab}}\)
\(\dfrac{\sqrt{7x}}{\sqrt{5x} + \sqrt{x}}\)
- Answer
-
\(\dfrac{\sqrt{35} - \sqrt{7}}{4}\)
\(\dfrac{\sqrt{3y}}{\sqrt{2y} - \sqrt{y}}\)
Exercises for Review
Simplify \(x^8y^7 \dfrac{x^4y^8}{x^3y^4}\)
- Answer
-
\(x^9y^{11}\)
Solve the compound inequality \(-8 \le 7 - 5x \le -23\)
Construct the graph of \(y = \dfrac{2}{3}x - 4\)
- Answer
-
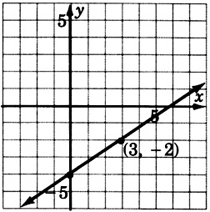
The symbol \(\sqrt{x}\) represents which square root of the number \(x, x \ge 0\)?
Simplify \(\sqrt{a^2 + 8a + 16}\)
- Answer
-
\(a + 4\)


