4.2E: Exercises

Last updated
Save as PDF

Page ID: 30120

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Practice Makes Perfect

Recognize the Relationship Between the Solutions of an Equation and its Graph

In the following exercises, for each ordered pair, decide:

Is the ordered pair a solution to the equation?
Is the point on the line?

Exercise $\PageIndex{1}$

y=x+2

(0,2)
(1,2)
(−1,1)
(−3,−1)

$The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, negative 4), (negative 5, negative 3), (negative 4, negative 2), (negative 3, negative 1), (negative 2, 0), (negative 1, 1), (0, 2), (1, 3), (2, 4), (3, 5), (4, 6), and (5, 7).$

Answer

yes; no
no; no
yes; yes
yes; yes

Exercise $\PageIndex{2}$

y=x−4

(0,−4)
(3,−1)
(2,2)
(1,−5)

$The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 3, negative 7), (negative 2, negative 6), (negative 1, negative 5), (0, negative 4), (1, negative 3), (2, negative 2), (3, negative 1), (4, 0), (5, 1), (6, 2), and (7, 3).$

Exercise $\PageIndex{3}$

$y=\frac{1}{2} x-3$

(0,−3)
(2,−2)
(−2,−4)
(4,1)

$The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, negative 6), (negative 4, negative 5), (negative 2, negative 4), (0, negative 3), (2, negative 2), (4, negative 1), and (6, 0).$

Answer

yes; yes
yes; yes
yes; yes
no; no

Exercise $\PageIndex{4}$

$y=\frac{1}{3} x+2$

(0,2)
(3,3)
(−3,2)
(−6,0)

Graph a Linear Equation by Plotting Points

In the following exercises, graph by plotting points.

Exercise $\PageIndex{5}$

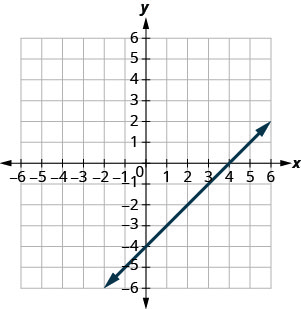
$y=3 x-1$

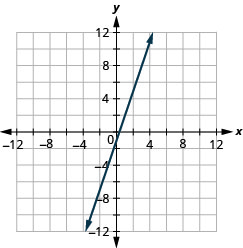
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 3, negative 10), (negative 2, negative 7), (negative 1, negative 4), (0, negative 1), (1, 2), (2, 5), and (3, 8).$

Exercise $\PageIndex{6}$

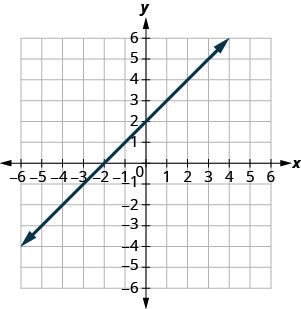
$y=2 x+3$

Exercise $\PageIndex{7}$

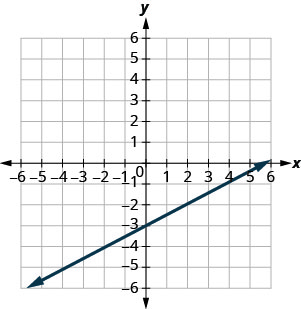
$y=-2 x+2$

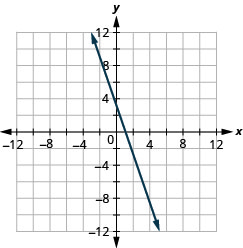
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 4, 10), (negative 3, 8), (negative 2, 6), (negative 1, 4), (0, 2), (1, 0), (2, negative 2), (3, negative 4), (4, negative 6), and (5, negative 8).$

Exercise $\PageIndex{8}$

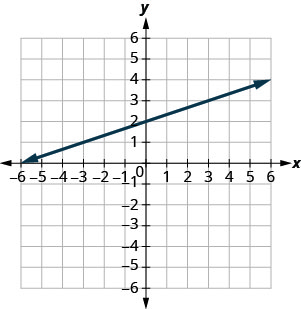
$y=-3 x+1$

Exercise $\PageIndex{9}$

$y=x+2$

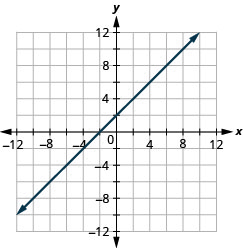
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, negative 8), (negative 9, negative 7), (negative 8, negative 6), (negative 7, negative 5), (negative 6, negative 4), (negative 5, negative 3), (negative 4, negative 2), (negative 3, negative 1), (negative 2, 0), (negative 1, 1), (0, 2), (1, 3), (2, 4), (3, 5), (4, 6), (5, 7), (6, 8), (7, 9), and (8, 10).$

Exercise $\PageIndex{10}$

$y=x-3$

Exercise $\PageIndex{11}$

$y=-x-3$

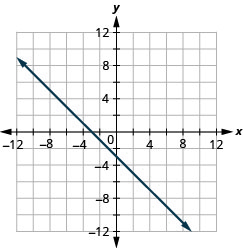
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, 7), (negative 9, 6), (negative 8, 5), (negative 7, 4), (negative 6, 3), (negative 5, 2), (negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), (4, negative 7), (5, negative 8), (6, negative 9), and (7, negative 10).$

Exercise $\PageIndex{12}$

$y=-x-2$

Exercise $\PageIndex{13}$

$y=2 x$

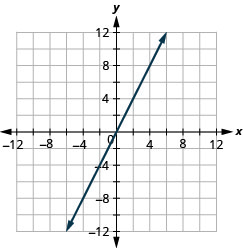
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 5, negative 10), (negative 4, negative 8), (negative 3, negative 6), (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4), (3, 6), (4, 8), and (5, 10).$

Exercise $\PageIndex{14}$

$y=3 x$

Exercise $\PageIndex{15}$

$y=-4 x$

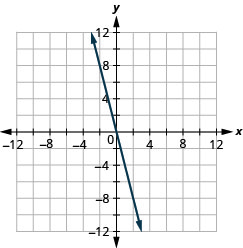
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 3, 12), (negative 2, 8), (negative 1, 4), (0, 0), (1, negative 4), (2, negative 8), and (3, negative 12).$

Exercise $\PageIndex{16}$

$y=-2 x$

Exercise $\PageIndex{17}$

$y=\frac{1}{2} x+2$

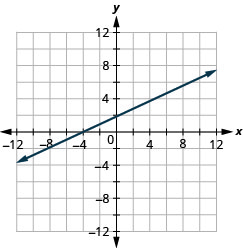
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 12, negative 4), (negative 10, negative 3), (negative 8, negative 2), (negative 6, negative 1), (negative 4, 0), (negative 2, 1), (0, 2), (2, 3), (4, 4), (6, 5), (8, 6), and (10, 7).$

Exercise $\PageIndex{18}$

$y=\frac{1}{3} x-1$

Exercise $\PageIndex{19}$

$y=\frac{4}{3} x-5$

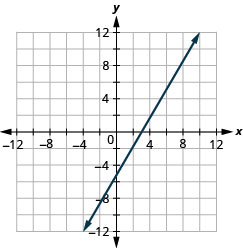
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 3, negative 9), (0, negative 5), (3, negative 1), (6, 3), and (9, 7).$

Exercise $\PageIndex{20}$

$y=\frac{3}{2} x-3$

Exercise $\PageIndex{21}$

$y=-\frac{2}{5} x+1$

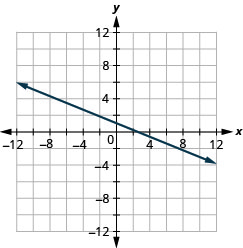
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, 5), (negative 5, 3), (0, 1), (5, negative 1), and (10, negative 3).$

Exercise $\PageIndex{22}$

$y=-\frac{4}{5} x-1$

Exercise $\PageIndex{23}$

$y=-\frac{3}{2} x+2$

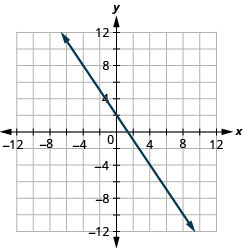
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 6, 11), (negative 4, 8), (negative 2, 5), (0, 2), (2, negative 1), (4, negative 4), (6, negative 7), and (8, negative 10).$

Exercise $\PageIndex{24}$

$y=-\frac{5}{3} x+4$

Exercise $\PageIndex{25}$

$x+y=6$

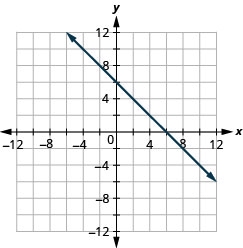
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 4, 10), (negative 3, 9), (negative 2, 8), (negative 1, 7), (0, 6), (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 0), (7, negative 1), (8, negative 2), (9, negative 3), and (10, negative 4).$

Exercise $\PageIndex{26}$

$x+y=4$

Exercise $\PageIndex{27}$

$x+y=-3$

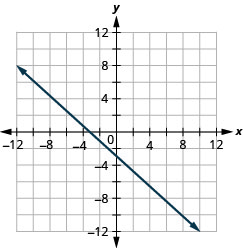
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, 7), (negative 9, 6), (negative 8, 5), (negative 7, 4), (negative 6, 3), (negative 5, 2), (negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), (4, negative 7), (5, negative 8), (6, negative 9), and (7, negative 10).$

Exercise $\PageIndex{28}$

$x+y=-2$

Exercise $\PageIndex{29}$

$x-y=2$

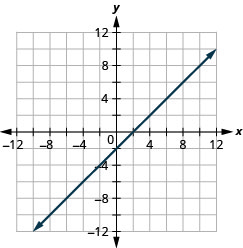
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 8, negative 10), (negative 7, negative 9), (negative 6, negative 8), (negative 5, negative 7), (negative 4, negative 6), (negative 3, negative 5), (negative 2, negative 4), (negative 1, negative 3), (0, negative 2), (1, negative 1), (2, 0), (3, 1), (4, 2), (5, 3), (6, 4), (7, 5), (8, 6), (9, 7), and (10, 8).$

Exercise $\PageIndex{30}$

$x-y=1$

Exercise $\PageIndex{31}$

$x-y=-1$

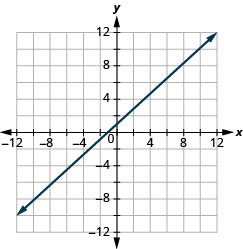
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 9, negative 8), (negative 8, negative 7), (negative 7, negative 6), (negative 6, negative 5), (negative 5, negative 4), (negative 4, negative 3), (negative 3, negative 2), (negative 2, negative 1), (negative 1, 0), (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9), and (9, 10).$

Exercise $\PageIndex{32}$

$x-y=-3$

Exercise $\PageIndex{33}$

$3 x+y=7$

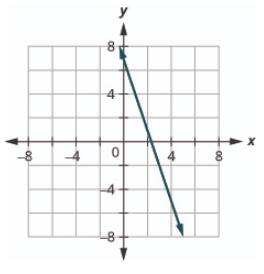
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to -7. The equation 3 x plus y equals 7 is graphed.$

Exercise $\PageIndex{34}$

$5x+y=6$

Exercise $\PageIndex{35}$

2x+y=−3

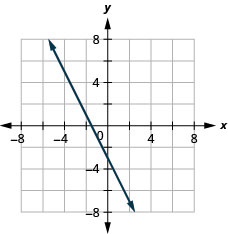
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 5, 7), (negative 4, 5), (negative 3, 3), (negative 2, 1), (negative 1, negative 1), (0, negative 3), (1, negative 5), and (2, negative 7).$

Exercise $\PageIndex{36}$

$4x+y=−5$

Exercise $\PageIndex{37}$

$\frac{1}{3} x+y=2$

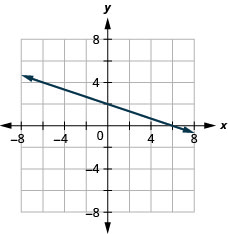
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 4), (negative 3, 3), (0, 2), (3, 1), and (6, 0).$

Exercise $\PageIndex{38}$

$\frac{1}{2} x+y=3$

Exercise $\PageIndex{39}$

$\frac{2}{5} x-y=4$

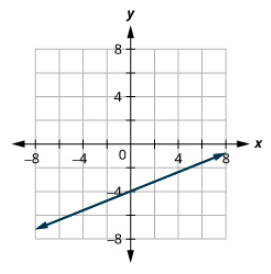
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 5, negative 2), (0, negative 4), and (5, negative 6).$

Exercise $\PageIndex{40}$

$\frac{3}{4} x-y=6$

Exercise $\PageIndex{41}$

$2 x+3 y=12$

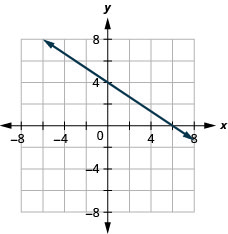
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 3, 6), (0, 4), (3, 2), and (6, 0).$

Exercise $\PageIndex{42}$

4x+2y=12

Exercise $\PageIndex{43}$

3x−4y=12

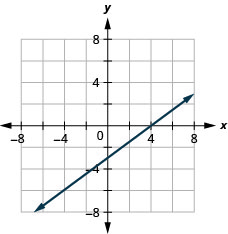
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 4, negative 6), (0, negative 3), (4, 0), and (8, 3).$

Exercise $\PageIndex{44}$

2x−5y=10

Exercise $\PageIndex{45}$

x−6y=3

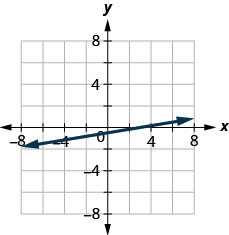
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, negative three halves), (negative 3, negative 1), (0, negative one half), (3, 0), and (6, one half).$

Exercise $\PageIndex{46}$

x−4y=2

Exercise $\PageIndex{47}$

5x+2y=4

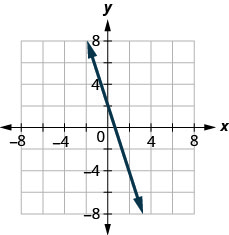
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 2, 7), (0, 2), (2, negative 3), and (4, negative 8).$

Exercise $\PageIndex{48}$

3x+5y=5

Graph Vertical and Horizontal Lines

In the following exercises, graph each equation.

Exercise $\PageIndex{49}$

x=4

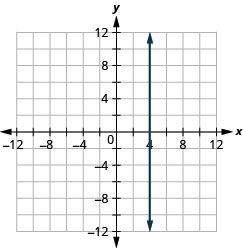
Answer: $The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The vertical line goes through the points (4, 0), (4, 1), (4, 2) and all points with first coordinate 4.$

Exercise $\PageIndex{50}$

x=3

Exercise $\PageIndex{51}$

x=−2

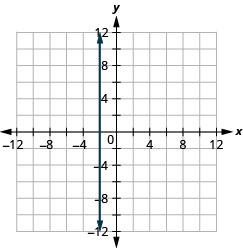
Answer: $The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The vertical line goes through the points (negative 2, 0), (negative 2, 1), (negative 2, 2) and all points with first coordinate negative 2.$

Exercise $\PageIndex{52}$

x=−5

Exercise $\PageIndex{53}$

y=3

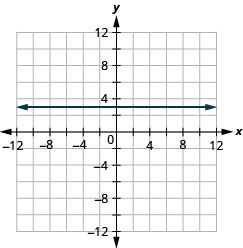
Answer: $The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The horizontal line goes through the points (0, 3), (1, 3), (2, 3) and all points with second coordinate 3.$

Exercise $\PageIndex{54}$

y=1

Exercise $\PageIndex{55}$

y=−5

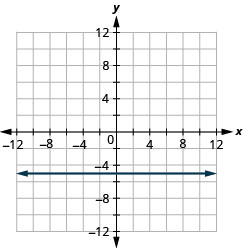
Answer: $The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The horizontal line goes through the points (0, negative 5), (1, negative 5), (2, negative 5) and all points with second coordinate negative 5.$

Exercise $\PageIndex{56}$

y=−2

Exercise $\PageIndex{57}$

$x=\frac{7}{3}$

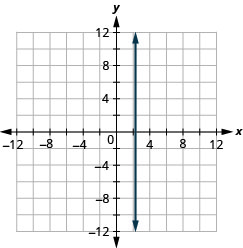
Answer: $The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The vertical line goes through the points (7/3, 0), (7/3, 1), (7/3, 2) and all points with first coordinate 7/3.$

Exercise $\PageIndex{58}$

$x=\frac{5}{4}$

Exercise $\PageIndex{59}$

$y=-\frac{15}{4}$

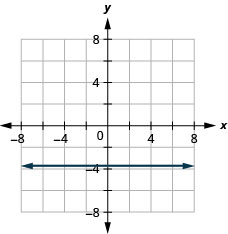
Answer: $The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The horizontal line goes through the points (0, negative 15/4), (1, negative 15/4), (2, negative 15/4) and all points with second coordinate negative 15/4.$

Exercise $\PageIndex{60}$

$y=-\frac{5}{3}$

In the following exercises, graph each pair of equations in the same rectangular coordinate system.

Exercise $\PageIndex{61}$

y=2x and y=2

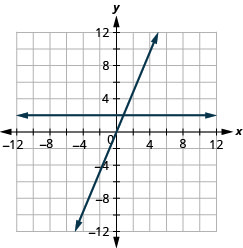
Answer: $The figure shows a two straight lines drawn on the same x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. One line is a straight horizontal line going through the points (negative 4, 2) (0, 2), (4, 2), and all other points with second coordinate 2. The other line is a slanted line going through the points (negative 5, negative 10), (negative 4, negative 8), (negative 3, negative 6), (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4), (3, 6), (4, 8), and (5, 10).$

Exercise $\PageIndex{62}$

y=5x and y=5

Exercise $\PageIndex{63}$

$y=-\frac{1}{2} x$ and $y=-\frac{1}{2}$

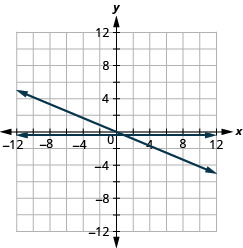
Answer: $The figure shows a two straight lines drawn on the same x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. One line is a straight horizontal line going through the points (negative 4, negative one half) (0, negative one half), (4, negative one half), and all other points with second coordinate negative one half. The other line is a slanted line going through the points (negative 10, 5), (negative 8, 4), (negative 6, 3), (negative 4, 2), (negative 2, 1), (0, 0), (1, negative 2), (2, negative 4), (3, negative 6), (4, negative 8), and (5, negative 10).$

Exercise $\PageIndex{64}$

$y=-\frac{1}{3} x$ and $y=-\frac{1}{3}$

Mixed Practice

In the following exercises, graph each equation.

Exercise $\PageIndex{65}$

y=4x

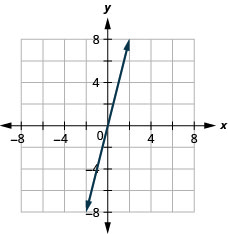
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 2, negative 8), (negative 1, negative 4), (0, 0), (1, 4), and (2, 8).$

Exercise $\PageIndex{66}$

y=2x

Exercise $\PageIndex{67}$

$y=-\frac{1}{2} x+3$

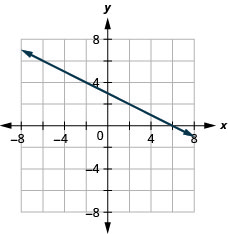
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 6), (negative 4, 5), (negative 2, 4), (0, 3), (2, 2), (4, 1), and (6, 0).$

Exercise $\PageIndex{68}$

$y=\frac{1}{4} x-2$

Exercise $\PageIndex{69}$

y=−x

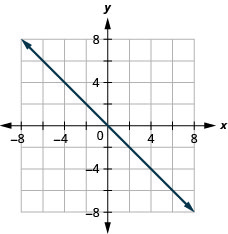
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 6), (negative 5, 5), (negative 4, 4), (negative 3, 3), (negative 2, 2), (negative 1, 1), (0, 0), (1, negative 1), (2, negative 2), (3, negative 3), (4, negative 4), (5, negative 5), and (6, negative 6).$

Exercise $\PageIndex{70}$

y=x

Exercise $\PageIndex{71}$

x−y=3

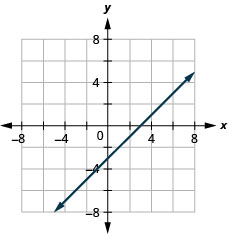
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 3, negative 7), (negative 2, negative 6), (negative 1, negative 4), (0, negative 3), (1, negative 2), (2, negative 1), (3, 0), (4, 1), (5, 2), and (6, 3).$

Exercise $\PageIndex{72}$

x+y=−5

Exercise $\PageIndex{73}$

4x+y=2

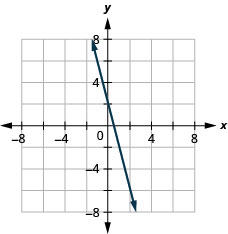
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 2, 6), (negative 1, 4), (0, 2), (1, negative 2), and (2, negative 6).$

Exercise $\PageIndex{74}$

2x+y=6

Exercise $\PageIndex{75}$

y=−1

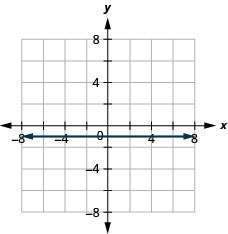
Answer: $The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The horizontal line goes through the points (0, negative 1), (1, negative 1), (2, negative 1) and all points with second coordinate negative 1.$

Exercise $\PageIndex{76}$

y=5

Exercise $\PageIndex{77}$

2x+6y=12

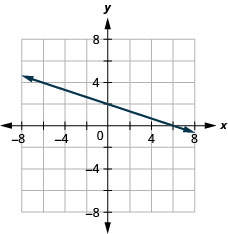
Answer: $The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 4), (negative 3, 3), (0, 2), (3, 1), and (6, 0).$

Exercise $\PageIndex{78}$

5x+2y=10

Exercise $\PageIndex{79}$

x=3

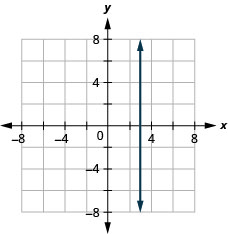
Answer: $The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The vertical line goes through the points (3, 0), (3, 1), (3, 2) and all points with first coordinate 3.$

Exercise $\PageIndex{80}$

x=−4

Everyday Math

Exercise $\PageIndex{81}$

Motor home cost. The Robinsons rented a motor home for one week to go on vacation. It cost them $594 plus $0.32 per mile to rent the motor home, so the linear equation y=594+0.32x gives the cost, yy, for driving xx miles. Calculate the rental cost for driving 400, 800, and 1200 miles, and then graph the line.

Answer

$722, $850, $978

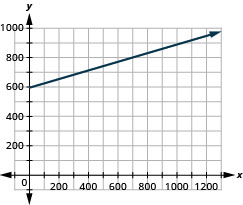
$The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from 0 to 1200 in increments of 100. The y-axis of the plane runs from 0 to 1000 in increments of 100. The straight line starts at the point (0, 594) and goes through the points (400, 722), (800, 850), and (1200, 978). The right end of the line has an arrow pointing up and to the right.$

Exercise $\PageIndex{82}$

Weekly earnings. At the art gallery where he works, Salvador gets paid $200 per week plus 15% of the sales he makes, so the equation y=200+0.15x gives the amount, yy, he earns for selling x dollars of artwork. Calculate the amount Salvador earns for selling $900, $1600, and $2000, and then graph the line.

Writing Exercises

Exercise $\PageIndex{83}$

Explain how you would choose three $x$ - values to make a table to graph the line $y=\frac{1}{5} x-2$

Answer: Answers will vary.

Exercise $\PageIndex{84}$

What is the difference between the equations of a vertical and a horizontal line?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This table has 4 rows and 4 columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is “Confidently”, the third is “With some help”, and the fourth is “No, I don’t get it”. Under the first column are the phrases “…recognize the relation between the solutions of an equation and its graph.”, “…graph a linear equation by plotting points.”, and “…graph vertical and horizontal lines.”. The other columns are left blank so that the learner may indicate their mastery level for each topic.$

ⓑ After reviewing this checklist, what will you do to become confident for all goals?

Practice Makes Perfect

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)

Exercise \(\PageIndex{31}\)

Exercise \(\PageIndex{32}\)

Exercise \(\PageIndex{33}\)

Exercise \(\PageIndex{34}\)

Exercise \(\PageIndex{35}\)

Exercise \(\PageIndex{36}\)

Exercise \(\PageIndex{37}\)

Exercise \(\PageIndex{38}\)

Exercise \(\PageIndex{39}\)

Exercise \(\PageIndex{40}\)

Exercise \(\PageIndex{41}\)

Exercise \(\PageIndex{42}\)

Exercise \(\PageIndex{43}\)

Exercise \(\PageIndex{44}\)

Exercise \(\PageIndex{45}\)

Exercise \(\PageIndex{46}\)

Exercise \(\PageIndex{47}\)

Exercise \(\PageIndex{48}\)

Exercise \(\PageIndex{49}\)

Exercise \(\PageIndex{50}\)

Exercise \(\PageIndex{51}\)

Exercise \(\PageIndex{52}\)

Exercise \(\PageIndex{53}\)

Exercise \(\PageIndex{54}\)

Exercise \(\PageIndex{55}\)

Exercise \(\PageIndex{56}\)

Exercise \(\PageIndex{57}\)

Exercise \(\PageIndex{58}\)

Exercise \(\PageIndex{59}\)

Exercise \(\PageIndex{60}\)

Exercise \(\PageIndex{61}\)

Exercise \(\PageIndex{62}\)

Exercise \(\PageIndex{63}\)

Exercise \(\PageIndex{64}\)

Mixed Practice

Exercise \(\PageIndex{65}\)

Exercise \(\PageIndex{66}\)

Exercise \(\PageIndex{67}\)

Exercise \(\PageIndex{68}\)

Exercise \(\PageIndex{69}\)

Exercise \(\PageIndex{70}\)

Exercise \(\PageIndex{71}\)

Exercise \(\PageIndex{72}\)

Exercise \(\PageIndex{73}\)

Exercise \(\PageIndex{74}\)

Exercise \(\PageIndex{75}\)

Exercise \(\PageIndex{76}\)

Exercise \(\PageIndex{77}\)

Exercise \(\PageIndex{78}\)