8.6E: Exercises
- Page ID
- 30271
Practice Makes Perfect
Solve Rational Equations
In the following exercises, solve.
\(\frac{1}{a}+\frac{2}{5}=\frac{1}{2}\)
- Answer
-
10
\(\frac{5}{6}+\frac{3}{b}=\frac{1}{3}\)
\(\frac{5}{2}−\frac{1}{c}=\frac{3}{4}\)
- Answer
-
\(\frac{4}{7}\)
\(\frac{6}{3}−\frac{2}{d}=\frac{4}{9}\)
\(\frac{4}{5}+\frac{1}{4}=\frac{2}{v}\)
- Answer
-
\(\frac{40}{21}\)
\(\frac{3}{7}+\frac{2}{3}=\frac{1}{w}\)
\(\frac{7}{9}+\frac{1}{x}=\frac{2}{3}\)
- Answer
-
−9
\(\frac{3}{8}+\frac{2}{y}=\frac{1}{4}\)
\(1−\frac{2}{m}=\frac{8}{m^2}\)
- Answer
-
−2, 4
\(1+\frac{4}{n}=\frac{21}{n^2}\)
\(1+\frac{9}{p}=−\frac{20}{p^2}\)
- Answer
-
−5, −4
\(1−\frac{7}{q}=−\frac{6}{q^2}\)
\(\frac{1}{r+3}=\frac{4}{2r}\)
- Answer
-
−6
\(\frac{3}{t−6}=\frac{1}{t}\)
\(\frac{5}{3v−2}=\frac{7}{4v}\)
- Answer
-
14
\(\frac{8}{2w+1}=\frac{3}{w}\)
\(\frac{3}{x+4}+\frac{7}{x−4}=\frac{8}{x^2−16}\)
- Answer
-
\(-\frac{4}{5}\)
\(\frac{5}{y−9}+\frac{1}{y+9}=\frac{18}{y^2−81}\)
\(\frac{8}{z−10}+\frac{7}{z+10}=\frac{5}{z^2−100}\)
- Answer
-
−13
\(\frac{9}{a+11}+\frac{6}{a−11}=\frac{7}{a^2−121}\)
\(\frac{1}{q+4}−\frac{7}{q−2}=1\)
- Answer
-
no solution
\(\frac{3}{r+10}−\frac{4}{r−4}=1\)
\(\frac{1}{t+7}−\frac{5}{t−5}=1\)
- Answer
-
−5, −1
\(\frac{2}{s+7}−\frac{3}{s−3}=1\)
\(\frac{v−10}{v^2−5v+4}=\frac{3}{v−1}−\frac{6}{v−4}\)
- Answer
-
no solution
\(\frac{w+8}{w^2−11w+28}=\frac{5}{w−7}+\frac{2}{w−4}\)
\(\frac{x−10}{x^2+8x+12}=\frac{3}{x+2}+\frac{4}{x+6}\)
- Answer
-
no solution
\(\frac{y−3}{y^2−4y−5}=\frac{1}{y+1}+\frac{8}{y−5}\)
\(\frac{z}{16}+\frac{z+2}{4z}=\frac{1}{2z}\)
- Answer
-
−4
\(\frac{a}{9}+\frac{a+3}{3a}=\frac{1}{a}\)
\(\frac{b+3}{3b}+\frac{b}{24}=\frac{1}{b}\)
- Answer
-
−8
\(\frac{c+3}{12c}+\frac{c}{36}=\frac{1}{4c}\)
\(\frac{d}{d+3}=\frac{18}{d^2−9}+4\)
- Answer
-
2
\(\frac{m}{m+5}=\frac{50}{m^2−25}+6\)
\(\frac{n}{n+2}=\frac{8}{n^2−4}+3\)
- Answer
-
1
\(\frac{p}{p+7}=\frac{98}{p^2−49}+8\)
\(\frac{q}{3q−9}−\frac{3}{4q+12}=\frac{7q^2+6q+63}{24q^2−216}\)
- Answer
-
no solution
\(\frac{r}{3r−15}−\frac{1}{4r+20}=\frac{3r^2+17r+40}{12r^2−300}\)
\(\frac{s}{2s+6}−\frac{2}{5s+5}=\frac{5s^2−3s−7}{10s^2+40s+30}\)
- Answer
-
no solution
\(\frac{t}{6t−12}−\frac{5}{2t+10}=\frac{t^2−23t+70}{12t^2+36t−120}\)
Solve a Rational Equation for a Specific Variable
In the following exercises, solve.
\(\frac{C}{r}=2π\) for r
- Answer
-
\(r=\frac{C}{2π}\)
\(\frac{I}{r}=P\) for r
\(\frac{V}{h}=lw\) for h
- Answer
-
\(h=\frac{v}{lw}\)
\(\frac{2A}{b}=h\) for b
\(\frac{v+3}{w−1}=\frac{1}{2}\) for w
- Answer
-
w=2v+7
\(\frac{x+5}{2−y}=\frac{4}{3}\) for y
\(a=\frac{b+3}{c−2}\) for c
- Answer
-
\(c=\frac{b+3+2a}{a}\)
\(m=\frac{n}{2−n}\) for n
\(\frac{1}{p}+\frac{2}{q}=4\) for p
- Answer
-
\(p=\frac{q}{4q−2}\)
\(\frac{3}{s}+\frac{1}{t}=2\) for s
\(\frac{2}{v}+\frac{1}{5}=\frac{1}{2}\) for w
- Answer
-
\(w=\frac{15v}{10+v}\)
\(\frac{6}{x}+\frac{2}{3}=\frac{1}{y}\) for y
\(\frac{m+3}{n−2}=\frac{4}{5}\) for n
- Answer
-
\(n=\frac{5m+23}{m}\)
\(\frac{E}{c}=m^2\) for c
\(\frac{3}{x}−\frac{5}{y}=\frac{1}{4}\) for y
- Answer
-
\(y=\frac{20x}{12−x}\)
\(\frac{R}{T}=W\) for T
\(r=\frac{s}{3−t}\) for t
- Answer
-
\(t=\frac{3r−s}{r}\)
\(c=\frac{2}{a}+\frac{b}{5}\) for a
Everyday Math
House Painting Alain can paint a house in 4 days. Spiro would take 7 days to paint the same house. Solve the equation \(\frac{1}{4}+\frac{1}{7}=\frac{1}{t}\) for t to find the number of days it would take them to paint the house if they worked together.
- Answer
-
\(2\frac{6}{11}\) days
Boating Ari can drive his boat 18 miles with the current in the same amount of time it takes to drive 10 miles against the current. If the speed of the boat is 7 knots, solve the equation \(\frac{18}{7+c}=\frac{10}{7−c}\) for c to find the speed of the current.
Writing Exercises
Why is there no solution to the equation \(\frac{3}{x−2}=\frac{5}{x−2}\)
- Answer
-
Answers will vary.
Pete thinks the equation \(\frac{y}{y+6}=\frac{72}{y^2−36}+4\) has two solutions, y=−6 and y=4. Explain why Pete is wrong.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
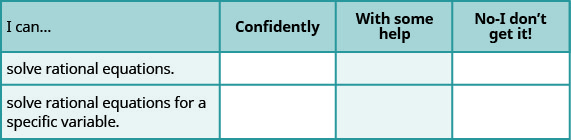
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?


