10.2E: Exercises
- Page ID
- 30284
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Complete the Square of a Binomial Expression
In the following exercises, complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.
\(a^2+10a\)
- Answer
-
\((a+5)^2\)
\(b^2+12b\)
\(m^2+18m\)
- Answer
-
\((m+9)^2\)
\(n^2+16n\)
\(m^2−24m\)
- Answer
-
\((m−12)^2\)
\(n^2−16n\)
\(p^2−22p\)
- Answer
-
\((p−11)^2\)
\(q^2−6q\)
\(x^2−9x\)
- Answer
-
\((x−\frac{9}{2})^2\)
\(y^2+11y\)
\(p^2−13p\)
- Answer
-
\((p−16)^2\)
\(q^2+34q\)
In the following exercises, solve by completing the square.
\(v^2+6v=40\)
- Answer
-
\(v=−10\), \(v=4\)
\(w^2+8w=65\)
\(u^2+2u=3\)
- Answer
-
\(u=−3\), \(u=1\)
\(z^2+12z=−11\)
\(c^2−12c=13\)
- Answer
-
\(c=−1\), \(c=13\)
\(d^2−8d=9\)
\(x^2−20x=21\)
- Answer
-
\(x=−1\), \(x=21\)
\(y^2−2y=8\)
\(m^2+4m=−44\)
- Answer
-
no real solution
\(n^2−2n=−3\)
\(r^2+6r=−11\)
- Answer
-
no real solution
\(t^2−14t=−50\)
\(a^2−10a=−5\)
- Answer
-
\(a=5\pm2\sqrt{5}\)
\(b^2+6b=41\)
\(u^2−14u+12=−1\)
- Answer
-
\(u=1\), \(u=13\)
\(z^2+2z−5=2\)
\(v^2=9v+2\)
- Answer
-
\(v=\frac{9}{2}\pm\frac{\sqrt{89}}{2}\)
\(w^2=5w−1\)
\((x+6)(x−2)=9\)
- Answer
-
\(x=−7\), \(x=3\)
\((y+9)(y+7)=79\)
Solve Quadratic Equations of the Form \(ax^2+bx+c=0\) by Completing the Square
In the following exercises, solve by completing the square.
\(3m^2+30m−27=6\)
- Answer
-
\(m=−11\), \(m=1\)
\(2n^2+4n−26=0\)
\(2c^2+c=6\)
- Answer
-
\(c=−2\), \(c=\frac{3}{2}\)
\(3d^2−4d=15\)
\(2p^2+7p=14\)
- Answer
-
\(p=−\frac{7}{4}\pm\frac{\sqrt{161}}{4}\)
\(3q^2−5q=9\)
Everyday Math
Rafi is designing a rectangular playground to have an area of 320 square feet. He wants one side of the playground to be four feet longer than the other side. Solve the equation \(p^2+4p=320\) for p, the length of one side of the playground. What is the length of the other side.
- Answer
-
16 feet, 20 feet
Yvette wants to put a square swimming pool in the corner of her backyard. She will have a 3 foot deck on the south side of the pool and a 9 foot deck on the west side of the pool. She has a total area of 1080 square feet for the pool and two decks. Solve the equation \((s+3)(s+9)=1080\) for s, the length of a side of the pool.
Writing Exercises
Solve the equation \(x^2+10x=−2\)
- by using the Square Root Property and
- by completing the square.
- Which method do you prefer? Why?
- Answer
-
- −5
- −5
- Answers will vary.
Solve the equation \(y^2+8y=48\) by completing the square and explain all your steps.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
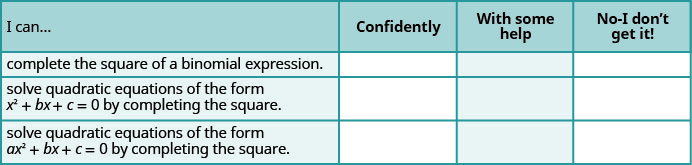
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?