8.3: Applications of Exponential Functions
- Page ID
- 19729
In the preceding section, we examined a population growth problem in which the population grew at a fixed percentage each year. In that case, we found that the population can be described by an exponential function. A similar analysis will show that any process in which a quantity grows by a fixed percentage each year (or each day, hour, etc.) can be modeled by an exponential function. Compound interest is a good example of such a process.
Discrete Compound Interest
If you put money in a savings account, then the bank will pay you interest (a percentage of your account balance) at the end of each time period, typically one month or one day. For example, if the time period is one month, this process is called monthly compounding. The term compounding refers to the fact that interest is added to your account each month and then in subsequent months you earn interest on the interest. If the time period is one day, it’s called daily compounding.
Let’s look at monthly compounding in more detail. Suppose that you deposit $100 in your account, and the bank pays interest at an annual rate of 5%. Let the function P(t) represent the amount of money that you have in your account at time t, where we measure t in years. We will start time at t = 0 when the initial amount, called the principal, is $100. In other words, P(0) = 100.
In the discussion that follows, we will compute the account balance at the end of each month. Since one month is \(\frac{1}{12}\) of a year, \(P(\frac{1}{12})\) represents the balance at the end of the first month, \(P(\frac{2}{12})\) represents the balance at the end of the second month, etc.
At the end of the first month, interest is added to the account balance. Since the annual interest rate 5%, the monthly interest rate is \(\frac{5%}{12}\), or \(\frac{.05}{12}\) in decimal form. Although we could approximate \(\frac{.05}{12}\) by a decimal, it will be more useful, as well as more accurate, to leave it in this form. Therefore, at the end of the first month, the interest earned will be \(100(\frac{.05}{12})\), so the total amount will be
\(P(\frac{1}{12}) = 100+100(\frac{.05}{12}) =100(1+\frac{.05}{12})\). (1)
Now at the end of the second month, you will have the amount that you started that month with, namely \(P(\frac{1}{12})\), plus another month’s worth of interest on that amount. Therefore, the total amount will be
\(P(\frac{2}{12}) = P(\frac{1}{12})+P(\frac{1}{12})(\frac{.05}{12}) = P(\frac{1}{12})(1+\frac{.05}{12})\). (2)
If we replace \(P(\frac{1}{12})\) in equation (2) with the result found in equation (1), then
\(P(\frac{2}{12})=100(1+\frac{.05}{12})(1+\frac{.05}{12}) = 100(1+ \frac{.05}{12})^2\). (3)
Let’s iterate one more month. At the end of the third month, you will have the amount that you started that month with, namely \(P(\frac{2}{12})\), plus another month’s worth of interest on that amount. Therefore, the total amount will be
\(P(\frac{3}{12}) = P(\frac{2}{12}) + P(\frac{2}{12})(\frac{.05}{12}) = P(\frac{2}{12})(1+\frac{.05}{12})\). (4)
However, if we replace \(P(\frac{2}{12})\) in equation (4) with the result found in equation (3), then
\(P(\frac{3}{12}) = 100(1+\frac{.05}{12})^2(1+\frac{.05}{12}) = 100(1+\frac{.05}{12})^3\). (5)
The pattern should now be clear. The amount of money you will have in the account at the end of m months is given by the function
\(P(\frac{m}{12}) = 100(1+\frac{.05}{12})^m\).
We can rewrite this formula in terms of years t by replacing \(\frac{m}{12}\) by t. Then m = 12t, so the formula becomes
\(P(t) = 100(1+\frac{.05}{12})^{12t}\). (6)
What would be different if you had started with a principal of 200? By tracing over our previous steps, it should be easy to see that the new formula would be
\(P(t) = 200(1+\frac{.05}{12})^{12t}\).
Similarly, if the interest rate had been 4% per year instead of 5%, then we would have ended up with the formula
\(P(t) = 100(1+\frac{.04}{12})^{12t}\).
Thus, if we let \(P_{0}\) represent the principal, and r represent the annual interest rate (in decimal form), then we can generalize the formula to
\(P(t) = P_{0}(1+\frac{r}{12})^{12t}\). (7)
If the principal is $100, the annual interest rate is 5%, and interest is compounded monthly, how much money will you have after ten years?
In formula(7), let \(P_{0} = 100\), r = .05, and t = 10:
\(P(10) = 100(1+\frac{.05}{12})^{12 \cdot 10}\)
We can use our graphing calculator to approximate this solution, as shown in Figure 1.
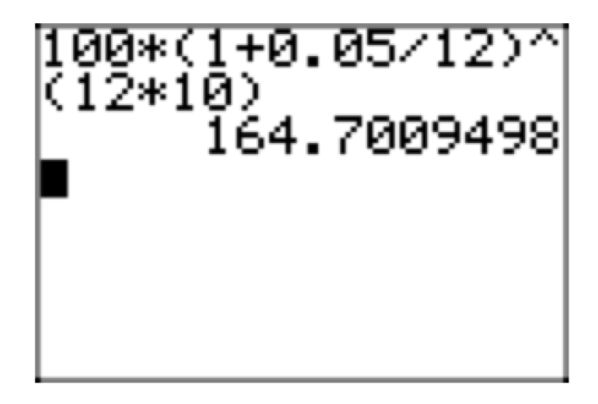
Thus, you would have $164.70 after ten years.
If the principal is $10000, the annual interest rate is 5%, and interest is compounded monthly, how much money will you have after forty years?
In formula (7), let \(P_{0} = 10000\), r = .05, and t = 40:
\(P(40) = 10000(1+\frac{.05}{12})^{12 \cdot 40} \approx 73584.17\)
Thus, you would have $73,584.17 after forty years.
These examples illustrate the “miracle of compound interest.” In the last example, your account is more than seven times as large as the original, and your total “profit” (the amount of interest you’ve received) is $63584.17. Compare this to the amount you would have received if you had withdrawn the interest each month (i.e., no compounding). In that case, your “profit” would only be $20000:
\(years \cdot \frac{months}{year} \cdot \frac{interest}{month} = 40 \cdot 12 \cdot [(10000)(\frac{.05}{12})] =20000\)
The large difference can be attributed to the shape of the graph of the function P(t). Recall from the preceding section that this is an exponential growth function, so as t gets large, the graph will eventually rise steeply. Thus, if you can leave your money in the bank long enough, it will eventually grow dramatically.
What about daily compounding? Let’s again analyze the situation in which the principal is $100 and the annual interest rate is 5%. In this case, the time period over which interest is paid is one day, or \(\frac{1}{365}\) of a year, and the daily interest rate is \(\frac{5%}{365}\), or \(\frac{.05}{365}\) in decimal form. Since we are measuring time in years, \(P(\frac{1}{365})\) represents the balance at the end of the first day, \(P(\frac{2}{365})\) represents the balance at the end of the second day, etc. We’ll follow the same steps as in the earlier analysis for monthly compounding.
At the end of the first day, you will have
\(P(\frac{1}{365}) = 100+100(\frac{.05}{365}) = 100(1+\frac{.05}{365})\). (10)
At the end of the second day, you will have the amount that you started that day with, namely \(P(\frac{1}{365})\), plus another day’s worth of interest on that amount. Therefore, the total amount will be
\(P(\frac{2}{365}) = P(\frac{1}{365})+P(\frac{1}{365})(\frac{.05}{365}) = P(\frac{1}{365})(1+\frac{.05}{365})\). (11)
If we replace \(P(\frac{1}{365})\) in equation (11) with the result found in equation (10), then
\(P(\frac{2}{365})=100(1+\frac{.05}{365})(1+\frac{.05}{365}) = 100(1+\frac{.05}{365}^2\). (12)
At the end of the third day, you will have the amount that you started that day with, namely \(P(\frac{2}{365})\), plus another day’s worth of interest on that amount. Therefore, the total amount will be
\(P(\frac{3}{365}) = P(\frac{2}{365})+P(\frac{2}{365})(\frac{.05}{365}) = P(\frac{2}{365})(1+\frac{.05}{365})\). (13)
Again, replacing \(P(\frac{2}{365})\) in equation (13) with the result found in equation (12)yields
\(P(\frac{3}{365})=100(1+\frac{.05}{365})^{2}(1+\frac{.05}{365}) = 100(1+\frac{.05}{365})^3\). (14)
Continuing this pattern shows that the amount of money you will have in the account at the end of d days is given by the function
\(P(\frac{d}{365}) = 100(1+\frac{.05}{365})^d\).
We can rewrite this formula in terms of years t by replacing \(\frac{d}{365}\) by t. Then d = 365t, so the formula becomes
\(P(t) = 100(1+\frac{.05}{365})^{365t}\). (15)
More generally, if you had started with a principal of \(P_{0}\) and an annual interest rate of r (in decimal form), then the formula would be
\(P(t) = P_{0}(1+\frac{r}{365})^{365t}\). (16)
Comparing formulas (7) and (16) for monthly and daily compounding, it should be apparent that the only difference is that the number 12 is used in the monthly compounding formula and the number 365 is used in the daily compounding formula. Looking at the respective analysis shows that this number arises from the portion of the year that interest is paid (\(\frac{1}{12}\) in the case of monthly compounding, and \(\frac{1}{365}\) in the case of daily compounding). Thus, in each case, this number (12 or 365) also equals the number of times that interest is compounded per year. It follows that if interest is compounded quarterly (every three months, or 4 times per year), the formula would be
\(P(t)=P_{0}(1+\frac{r}{4})^{4t}\).
Similarly, if interest is compounded hourly (8760 times per year), the formula would be
\(P(t) = P_{0}(1+\frac{r}{8760})^{8760t}\).
Summarizing, we have one final generalization:
If \(P_{0}\) is the principal, r is the annual interest rate, and n is the number of times that interest is compounded per year, then the balance at time t years is
\(P(t) = P_{0}(1+\frac{r}{n})^{nt}\). (17)
If the principal is $100, the annual interest rate is 5%, and interest is compounded daily, what will be the balance after ten years?
In formula (17), let \(P_{0} = 100\), r = .05, n = 365, and t = 10:
\(P(10) = 100(1+\frac{.05}{365})^{365 \cdot 10} \approx 164.87\)
Thus, you would have $164.87 after ten years.
If the principal is $10000, the annual interest rate is 5%, and interest is compounded daily, what will be the balance after forty years?
In formula (17), let \(P_{0} = 10000\), r = .05, n = 365, and t = 40:
\(P(40) = 10000(1+\frac{.05}{365})^{365 \cdot 40} \approx 73880.44\)
Thus, you would have $73880.44 after forty years.
As you can see from comparing Examples 8 and 18, and Examples 9 and 19, the difference between monthly and daily compounding is generally small. However, the difference can be substantial for large principals and/or large time periods.
If the principal is $500, the annual interest rate is 8%, and interest is compounded quarterly, what will be the balance after 42 months?
42 months is 3.5 years, so let \(P_{0} = 500\), r = .08 , n = 4, and t = 3.5 in formula(17):
\(P(3.5) = 500(1+\frac{.08}{4})^{4 \cdot 3.5} \approx 659.74\)
Thus, you would have $659.74 after 42 months.
Continuous Compound Interest and the Number e
Using formula (17), it is a simple matter to calculate the total amount for any type of compounding. Although most banks compound interest either daily or monthly, it could be done every hour, or every minute, or every second, etc. What happens to the total amount as the time period shortens? Equivalently, what happens as n increases in formula (17)? Table 1 shows the amount after one year with a principal of \(P_{0} = 100\), r = .05, and various values of n:
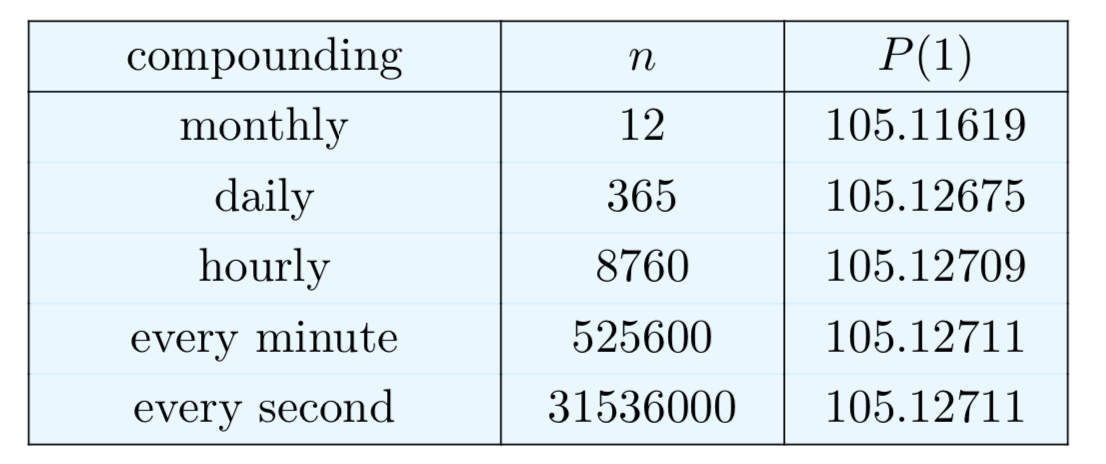
Table 1. Comparison of discrete compounding with \(P_{0} = 100\), r = .05, and t = 1 year.
Even if we carry out our computations to eight digits, it appears that the amounts in the right hand column of Table 1 are stabilizing. In fact, using calculus, it can be shown that these amounts do indeed get closer and closer to a particular number, and we can calculate that number.
Starting with formula (17), we will let n approach \(\infty\). In other words, we will let n get larger and larger without bound, as we started to do in Table 1. The first step is to use the Laws of Exponents to write
\(P_{0}(1+\frac{r}{n})^{nt} = P_{0}[(1+\frac{r}{n})^{\frac{n}{r}}]^{rt}\)
In the next step, replace \(frac{n}{r}\) by m. Since \(\frac{n}{r} = m\), it follows that \(\frac{r}{n} = \frac{1}{m}\), and we have
\(P_{0}[(1+\frac{r}{n})^{\frac{n}{r}}]^{rt} = P_{0}[(1+\frac{1}{m})^{m}]^{rt}\)
Now let n approach \(\infty\). Since \(m = \frac{n}{r}\) and r is fixed, it follows that m also approaches \(\infty\). We can use the TABLE feature of the graphing calculator to investigate the convergence of the expression in brackets as m approaches infinity.
- Load \((1+\frac{1}{m})^m\) into the Y= menu of the graphing calculator, as shown in Figure 2(a). Of course, you must use x instead of m and enter (1+1/X)^X.
- Use TBLSET and set Indepnt to Ask, select TABLE, then enter the numbers 10, 100,1000, 10000, 100000, and 1000000 to produce the result shown in Figure 2(b). Note that (1+1/X)^X appears to converge to the number 2.7183. If you move the cursor over the last result in the Y1 column, you can see more precision,2.71828046932.
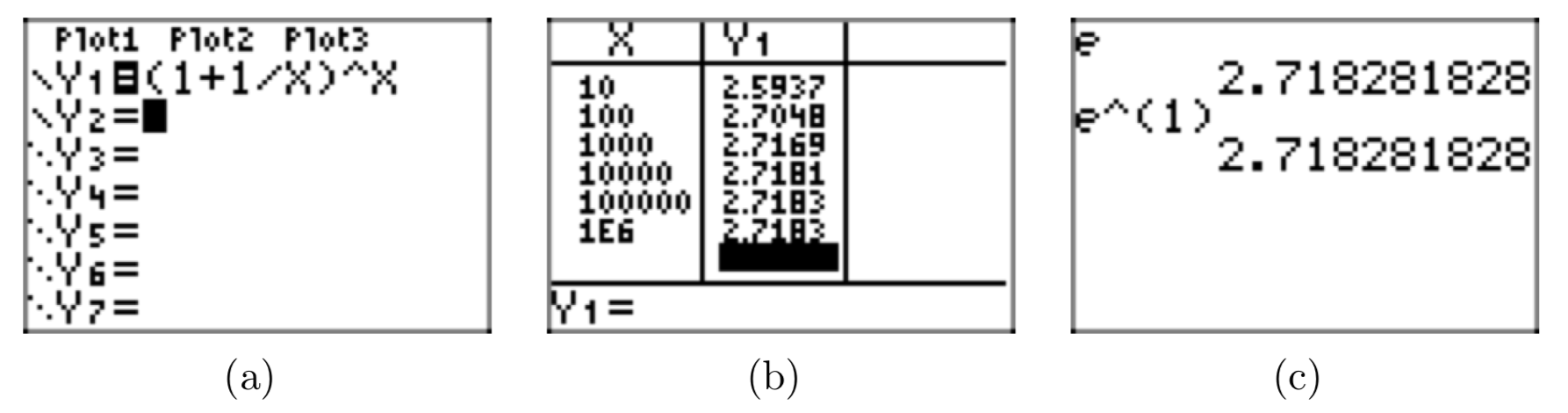
Note that the numbers in the second column in Figure 2(b) appear to stabilize. Indeed, it can be shown by using calculus that the expression in brackets above gets closer and closer to a single number, which is called e. To represent this convergence, we write
\(1+\frac{1}{m})^m \rightarrow e\)
e is an irrational number, approximately 2.7183, as shown by the computations in Figure 2(b). It follows that
\(P_{0}[(1+\frac{1}{m})^{m}]^{rt} \rightarrow P_{0}e^{rt}\)
If \(P_{0}\) is the principal, r is the annual interest rate, and interest is compounded continuously, then the balance at time t years is
\(P(t) = P_{0}e^{rt}\)
Before working the next examples, find the buttons on your calculator for the number e and for the exponential function \(e^x\). Typing either e or e^(1) (using the \(e^x\)button) will yield an approximation to the number e, as shown in Figure 2(c). Compare this approximation with the one you obtained earlier in Figure 2(b).
If the principal is $100, the annual interest rate is 5%, and interest is compounded continuously, what will be the balance after ten years?
In formula (22), let \(P_{0} = 100\), r = 0.05, and t = 10:
\(P (10) = 100e^{(0.05)(10)}\)
Use your calculator to approximate this result, as shown in Figure 3.
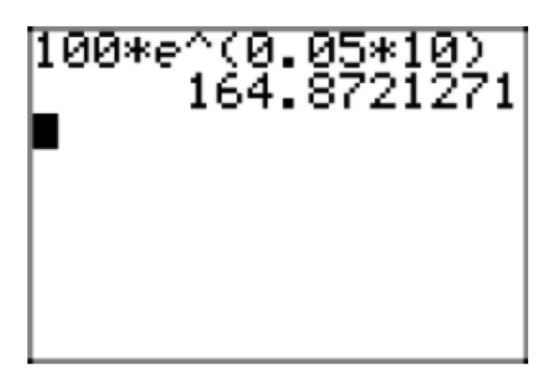
Thus, you would have $164.87 after ten years.
If the principal is $10,000, the annual interest rate is 5%, and interest is compounded continuously, what will be the balance after forty years?
In formula (22), let \(P_{0} = 10000\), r = 0.05, and t = 40:
\(P (10) = 10000e^{(0.05)(40)} \approx 73 890.56\)
Thus, you would have $73 890.56 after forty years.
Notice that the continuous compounding formula (22) is much simpler than the discrete compounding formula (17). Unless the principal is very large or the time period is very long, the preceding examples show that continuous compounding is also a close approximation to daily compounding. In Example 23, the amount $164.87 is the same (rounded to the nearest cent) as the amount for daily compounding found in Example 18. With a larger principal and longer time period, the amount $73 890.56 in Example 24 using continuous compounding is still only about $10 more than the amount $73 880.44 for daily compounding found in Example 19.
- The number e may strike you as a mere curiosity. If so, that would be a big misconception. The number e is actually one of the most important numbers in mathematics (it’s probably the second most famous number, following π), and it arises naturally as the limit described in (21) above. Using notation from calculus, we write
\(lim_{m \rightarrow \infty} (1 +\frac{1}{m})^m = e \approx 2.71828\). (26)
Although in our discussion above this limit arose in a man-made process, compound interest, it shows up in a similar manner in studies of many natural phenomena. We’ll look at some of these applications later in this chapter.
2. Likewise, the exponential function ex is one of the most important functions used in mathematics, statistics, and many fields of science. For a variety of reasons, the base e turns out to be the most natural base to use for an exponential function. Consequently, the function \(f(x) = e^x\) is known as the natural exponential function.
Future Value and Present Value
In this section we have derived two formulas, one for discrete compound interest, and the other for continuous compound interest. However, in the examples presented so far, we’ve only used these formulas to calculate future value: given a principal P0 and interest rate r, how much will you have in your account in t years?
Another type of question we can solve is known as a present value problem: how much money would you have to invest at interest r in order to have Q dollars in t years? Here are a couple of examples:
How much money would you have to invest at 4% interest compounded daily in order to have $8000 dollars in 6 years?
In this case, the principal \(P_{0}\) is unknown, and we substitute r = 0.04, n = 365, and t = 6, into the discrete compounding formula (17). Since P(6) = 8000, we have the equation
\(8000 = P(6) = P_{0}(1+\frac{0.04}{365})^{(365)(5)}\)
This equation can be solved by division:
\(\frac{8000}{1+\frac{0.04}{365}} = P_{0}\)
Figure 4 shows a calculator approximation for this result.
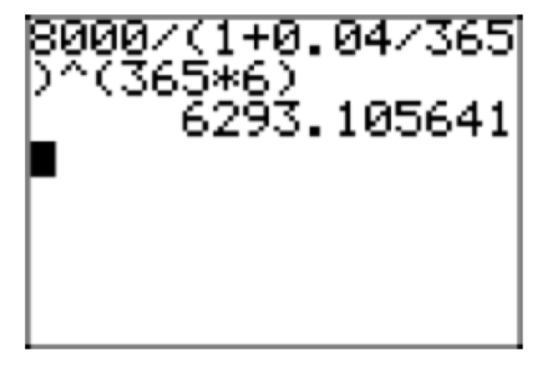
Thus, the present value is approximately \(P_{0} \approx $6293.11\). If this amount is invested now at 4% compounded daily, then its future value in 6 years will be $8000.
How much money would you have to invest at 7% interest compounded continuously in order to have $5000 dollars in 4 years?
As in the last example, the principal \(P_{0}\) is unknown, and this time r = 0.07 and t = 4 in the continuous compounding formula (22). Then P(4) = 5000 yields the equation
\(5000 = P(4) = P_{0}e^{(0.07)(4)}\).
As in the last example, this equation can also be solved by division:
\(\frac{5000}{e^{(0.07)(4)}} = P_{0}\)
A calculator approximation for this result is shown in Figure 5.
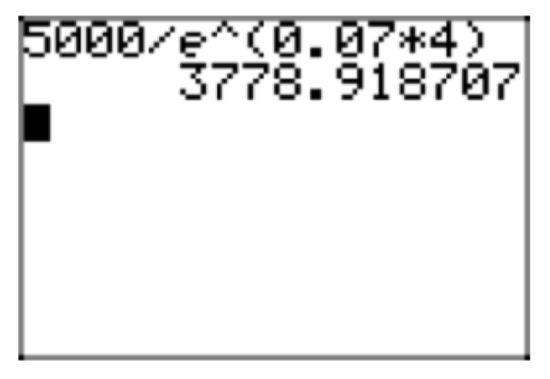
Thus, the present value is approximately \(P_{0} \approx $3778.92\). If this amount is invested now at 7% compounded continuously, then its future value in 4 years will be $5000.
Additional Questions
In terms of practical applications, there are also other types of questions that would be interesting to consider. Here are two examples:
- If you deposit $1000 in an account paying 6% compounded continuously, how long will it take for you to have $1500 in your account?
- If you deposit $1000 in an account paying 5% compounded monthly, how long will it take for your money to double?
Let’s look at the first question (the second is similar). In this case, \(P_{0} = 1000\) and r = 0.06. Inserting these values into the continuous compounding formula (22), we obtain
\(P(t) = 1000e^{0.06t}\).
Now we want the future value P(t) of the account at some time t to equal $1500.
Therefore, we must solve the equation
\(1500 = 1000e^{0.06t}\).
However, now we have a problem, because the variable t is located in the exponent of the expression on the right side of the equation. Although we could approximate a solution graphically, we currently have no algebraic method for solving an equation such as this, where the variable is in the exponent (these types of equations are called exponential equations). Over the course of the next few sections, we will define another type of function, the logarithm function, which will in turn provide us with a method for solving exponential equations. Then we will return to these questions, and also discuss additional applications.
Exercise
Suppose that you invest $15,000 at 7% interest compounded monthly. How much money will be in your account in 4 years? Round your answer to the nearest cent.
- Answer
-
$19830.81
Suppose that you invest $14,000 at 3% interest compounded monthly. How much money will be in your account in 7 years? Round your answer to the nearest cent.
Suppose that you invest $14,000 at 4% interest compounded daily. How much money will be in your account in 6 years? Round your answer to the nearest cent.
- Answer
-
$17797.25
Suppose that you invest $15,000 at 8% interest compounded monthly. How much money will be in your account in 8 years? Round your answer to the nearest cent.
Suppose that you invest $4,000 at 3% interest compounded monthly. How much money will be in your account in 7 years? Round your answer to the nearest cent.
- Answer
-
$4933.42
Suppose that you invest $3,000 at 5% interest compounded monthly. How much money will be in your account in 4 years? Round your answer to the nearest cent.
Suppose that you invest $1,000 at 3% interest compounded monthly. How much money will be in your account in 4 years? Round your answer to the nearest cent.
- Answer
-
$1127.33
Suppose that you invest $19,000 at 2% interest compounded daily. How much money will be in your account in 9 years? Round your answer to the nearest cent.
Suppose that you can invest money at 4% interest compounded monthly. How much should you invest in order to have $20,000 in 2 years? Round your answer to the nearest cent.
- Answer
-
$18464.78
Suppose that you can invest money at 6% interest compounded daily. How much should you invest in order to have $1,000 in 2 years? Round your answer to the nearest cent.
Suppose that you can invest money at 3% interest compounded daily. How much should you invest in order to have $20,000 in 3 years? Round your answer to the nearest cent.
- Answer
-
$18278.69
Suppose that you can invest money at 3% interest compounded monthly. How much should you invest in order to have $10,000 in 7 years? Round your answer to the nearest cent.
Suppose that you can invest money at 9% interest compounded daily. How much should you invest in order to have $4,000 in 9 years? Round your answer to the nearest cent.
- Answer
-
$1779.61
Suppose that you can invest money at 8% interest compounded daily. How much should you invest in order to have $18,000 in 6 years? Round your answer to the nearest cent.
Suppose that you can invest money at 8% interest compounded daily. How much should you invest in order to have $17,000 in 6 years? Round your answer to the nearest cent.
- Answer
-
$10519.87
Suppose that you can invest money at 9% interest compounded daily. How much should you invest in order to have $5,000 in 7 years? Round your answer to the nearest cent.
In Exercises 17-24, evaluate the function at the given value p. Round your answer to the nearest hundredth.
\(f(x) = e^x\); p = 1.57.
- Answer
-
4.81
\(f(x) = e^x\); p = 2.61.
\(f(x) = e^x\); p = 3.07.
- Answer
-
21.54
\(f(x) = e^x\); p = −4.33.
\(f(x) = e^x\); p = 1.42.
- Answer
-
4.14
\(f(x) = e^x\); p = −0.8.
\(f(x) = e^x\); p = 4.75
- Answer
-
115.58
\(f(x) = e^x\); p = 3.60.
Suppose that you invest $3,000 at 4% interest compounded continuously. How much money will be in your account in 9 years? Round your answer to the nearest cent.
- Answer
-
$4299.99
Suppose that you invest $8,000 at 8% interest compounded continuously. How much money will be in your account in 7 years? Round your answer to the nearest cent.
Suppose that you invest $1,000 at 2% interest compounded continuously. How much money will be in your account in 3 years? Round your answer to the nearest cent.
- Answer
-
$1061.84
Suppose that you invest $3,000 at 8% interest compounded continuously. How much money will be in your account in 4 years? Round your answer to the nearest cent.
Suppose that you invest $15,000 at 2% interest compounded continuously. How much money will be in your account in 4 years? Round your answer to the nearest cent.
- Answer
-
$16249.31
Suppose that you invest $8,000 at 2% interest compounded continuously. How much money will be in your account in 6 years? Round your answer to the nearest cent.
Suppose that you invest $13,000 at 9% interest compounded continuously. How much money will be in your account in 8 years? Round your answer to the nearest cent.
- Answer
-
$26707.63
Suppose that you invest $16,000 at 4% interest compounded continuously. How much money will be in your account in 6 years? Round your answer to the nearest cent.
Suppose that you can invest money at 6% interest compounded continuously. How much should you invest in order to have $17,000 in 9 years? Round your answer to the nearest cent.
- Answer
-
$9906.72
Suppose that you can invest money at 8% interest compounded continuously. How much should you invest in order to have $5,000 in 6 years? Round your answer to the nearest cent.
Suppose that you can invest money at 8% interest compounded continuously. How much should you invest in order to have $10,000 in 6 years? Round your answer to the nearest cent.
- Answer
-
$6187.83
Suppose that you can invest money at 6% interest compounded continuously. How much should you invest in order to have $17,000 in 13 years? Round your answer to the nearest cent.
Suppose that you can invest money at 2% interest compounded continuously. How much should you invest in order to have $13,000 in 8 years? Round your answer to the nearest cent.
- Answer
-
$11077.87
Suppose that you can invest money at 9% interest compounded continuously. How much should you invest in order to have $10,000 in 15 years? Round your answer to the nearest cent.
Suppose that you can invest money at 7% interest compounded continuously. How much should you invest in order to have $18,000 in 10 years? Round your answer to the nearest cent.
- Answer
-
$8938.54
Suppose that you can invest money at 9% interest compounded continuously. How much should you invest in order to have $14,000 in 12 years? Round your answer to the nearest cent.


