8.6: Properties of Logarithms; Solving Exponential Equations
- Page ID
- 19732
Logarithms were actually discovered and used in ancient times by both Indian and Islamic mathematicians. They were not used widely, though, until the 1600’s, when logarithms simplified the large amounts of hand computations needed in the scientific explorations of the times. In particular, after the invention of the telescope, calculations involving astronomical data became very important, and logarithms became an essential mathematical tool. Indeed, until the invention of the computer and electronic calculator in recent times, hand calculations using logarithms were a staple of every science student’s curriculum.
The usefulness of logarithms in calculations is based on the following three important properties, known generally as the properties of logarithms.
(a) \(log_{b}(MN) = log_{b}(M)+log_{b}(N)\)
(b) \(log_{b}(\frac{M}{N}) = log_{b}(M)−log_{b}(N)\)
(c) \(log_{b}(M^r)=rlog_{b}(M)\)
provided that M, N, b > 0.
The first property says that the “log of a product is the sum of the logs.” The second says that the “log of a quotient is the difference of the logs.” And the third property is sometimes referred to as the “power rule”. Loosely speaking, when taking the log of a power, you can just move the exponent out in front of the log.
We won’t go into the details of the computation procedures using properties (a) and (b), since these procedures are no longer necessary after the invention of the calculator. But the idea is that a time-consuming product of two numbers, for example two 10-digit numbers, can be transformed by property (a) into a much simpler addition problem. Similarly, a large and difficult quotient can be transformed by property (b) into a much simpler subtraction problem. Properties (a) and (b) are also the basis for the slide rule, a mechanical computation device that preceded the electronic calculator (very fast and useful, but only accurate to about three digits).
Property (c), on the other hand, is still useful for difficult computations. If you try to compute a large power, say 2100, on a calculator or computer, you’ll get an error message. That’s because all calculators and computers can only handle numbers and exponents within a certain range. So to compute a large power, it’s necessary to use property (c) to turn it into a multiplication problem. The details of this procedure are given in Section 8.8.
Even though properties (a) and (b) are no longer necessary for computation purposes, that does not mean they are not important. Logarithmic functions serve many purposes in mathematics and the sciences, and all of the logarithm properties are useful in various ways.
Where do the logarithm properties come from? Actually, they’re all derived from the laws of exponents, using the fact that the exponential function is the inverse of the logarithm function. Since we’ll only be using property (c) in this book, we’ll show how that property is derived. Properties (a) and (b) are derived in a similar manner.
Proof of (c): Start on the right side of the equation, and label \(log_{b}(M)\) by x:
\(x = log_{b}(M)\)
Use Definition 1 in Section 8.5 to rewrite the equation in exponential form:
\(b^x = M\)
Raise both sides to the rth power:
\((b^x)^r =M^r\)
Apply one of the Laws of Exponents to the left side:
\(b^{rx} = M^r\)
Apply the base b logarithmic function to both sides:
\(log_{b}(b^rx) = log_{b}(M^r)\)
Apply formula (10) in Section 8.5 to the left side:
\(rx = log_{b}(M^r)\)
Substitute back for x from the first line above:
\(rlog_{b}(M) = log_{b}(M^r)\)
This is the formula in property (c).
Change of Base Formula
We can now prove a conversion formula that will enable us to compute the logarithm to any base.
\(log_{a}(x) = \frac{log_{b}(x)}{log_{b}(a)}\)
Proof: Start on the left side of the equation, and label \(log_{a}(x)\) by r:
\(r = log_{a}(x)\)
Use Definition 1 in Section 8.5 to rewrite the equation in exponential form:
\(a^r = x\)
Apply the base b logarithmic function to both sides:
\(log_{b}(a^r) = log_{b}(x)\)
Apply property (c) to the left side:
\(rlog_{b}(a) = log_{b}(x)\)
Divide by \(log_{b}(a)\):
\(r = \frac{log_{b}(x)}{log_{b}(a)}\)
Substitute back for r from the first line above:
\(log_{a}(x) = \frac{log_{b}(x)}{log_{b}(a)}\)
This is the Change of Base Formula.
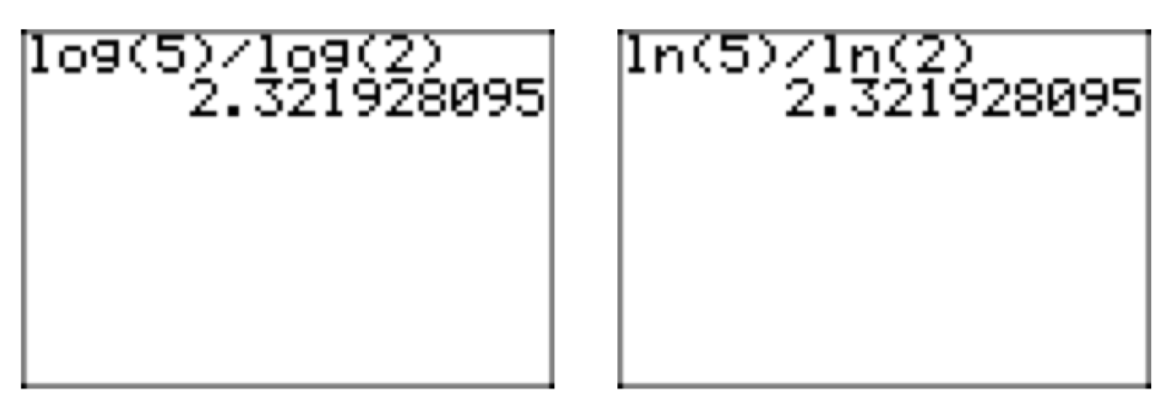
Compute \(log_{2}(5)\).
Before applying the Change of Base Formula, let’s see if we can estimate the value of \(log_{2}(5)\). First recall from Property 9 in Section 8.5 that \(2^{log_{2}(5)} = 5\). Now how large would the exponent on a base of 2 need to be for the power to equal 5? Since \(2^2 = 4\) (too small) and \(2^3 = 8\) (too large), we should expect \(log_{2}(5)\) to lie somewhere between 2 and 3. Indeed, applying the Change of Base Formula with the common logarithm yields
\(log_{2}(5) = \frac{log_{10}(5)}{log_{10}(5)} = \frac{log(5)}{log(2)} \approx \frac{.6989700043}{.3010299957} \approx 2.321928095\).
According to the formula, we could instead use the natural logarithm to obtain the same answer, as in
\(log_{2}(5) = \frac{log_{e}(5)}{log_{e}(2)} = \frac{ln(5)}{ln(2)} \approx \frac{1.609437912}{.6931471806} \approx 2.321928095\).
Calculator keystrokes are shown in Figure 1.
Another way to view the Change of Base Formula is that it says that all logarithms are multiples of each other, since
\(log_{a}(x) = (\frac{1}{log_{b}(a)})log_{b}(x)\).
Thus, \(log_{a}(x)\) is a constant multiple of \(log_{b}(x)\), where the constant is \(\frac{1}{log_{b}(a)}\).
Solving Exponential Equations
Property (c) (\(log_{b}(M^r) = r log_{b}(M)\)) is also used extensively to help solve exponential equations, and thus will be an important tool when we work with applications in the next section. In general terms, the main strategy for solving exponential equations is to (1) first isolate the exponential, then (2) apply a logarithmic function to both sides, and then (3) use property (c). We’ll illustrate the strategy with several examples.
Solve \(8 = 5(3^x)\).
Before trying the procedure outlined above, let’s first approximate the solution using a graphical approach. Graph both sides of the equation in your calculator, and then find the intersection of the two curves to obtain \(x \approx 0.42781574\) (see Figure 2).
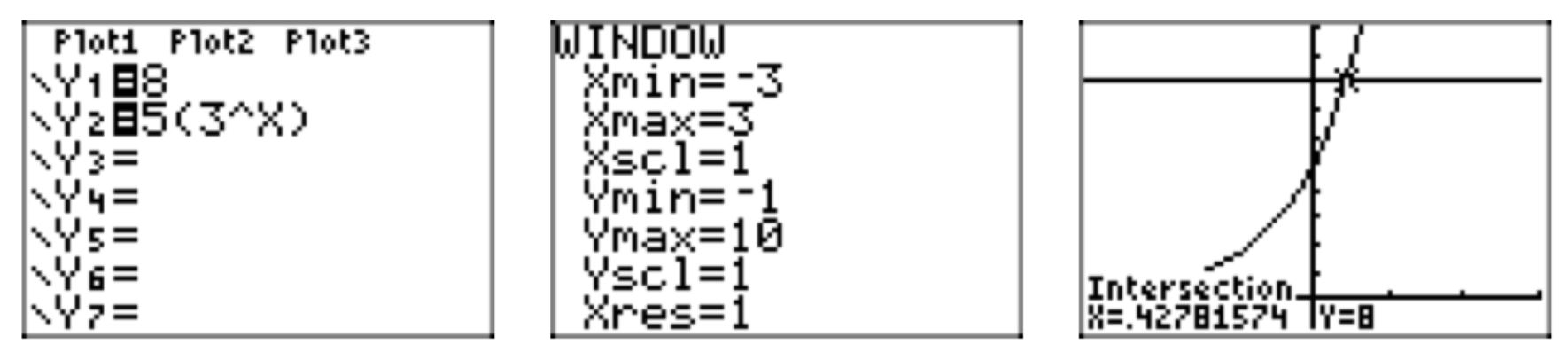
Now we’ll solve the equation algebraically. First isolate the exponential function on one side of the equation by dividing both sides by 5:
\(1.6 = 3^x\)
Then take the logarithm of both sides. Use either the common or natural log:
\(log(1.6) = log(3^x)\)
Now use property (c) to move the exponent in front of the log on the right side:
log(1.6) = xlog(3)
Finally, solve for x by dividing both sides by log(3):
\(\frac{log(1.6)}{log(3)} = x\)
Thus, the exact value of x is \(\frac{log(1.6)}{log(3)}\), and the approximate value is 0.42781574. Note that this is the same as the graphical approximation found earlier.
Solve \(300 = 100(1.05^{5x})\).
\(300 = 100(1.05^{5x})\)
\(\rightarrow 3 = 1.05^{5x}\) isolate the exponential
\(\rightarrow log(3) = log(1.05^{5x})\) apply the common log function
\(\rightarrow log(3) = 5x log(1.05)\) use property (c)
\(\rightarrow \frac{log(3)}{5log(1.05)} = x\) divide
\(\rightarrow x \approx 4.503417061\)
If the base of the exponential is either 10 or e, the correct choice of logarithm leads to a faster solution:
Solve \(3 = 4e^x\).
\(3 = 4e^x\).
\(\rightarrow 0.75 = e^x\) isolate the exponential
\(\rightarrow ln(0.75) = ln(e^x)\) apply the natural log function
\(\rightarrow ln(0.75) = x\) since \(ln(e^x) = x\)
\(\rightarrow x \approx −.2876820725\)
In this case, because the base of the exponential function is e, the use of the natural log function simplifies the solution.
We can now turn our attention to solving more interesting application problems, such as the questions raised at the end of Section 8.3.
If you deposit $1000 in an account paying 6% interest compounded continuously, how long will it take for you to have $1500 in your account?
First, recall the continuous compound interest formula from Section 8.3:
\(P(t) = P_{0}e^{rt}\) (6)
In this case, \(P_{0} = 1000\) and r = .06. Inserting these values into the formula, we obtain
\(P(t) = 1000e^{0.06t}\).
Now we want the future value P(t) of the account at some time t to equal $1500. Therefore, we must solve the equation
\(1500 = 1000e^{0.06t}\).
Following the steps in the previous example,
\(1500 = 1000e^{0.06t}\)
\(\rightarrow 1.5 = e^{0.06t}\) isolate the exponential
\(\rightarrow ln(1.5) = ln(e^{0.06t})\) apply the natural log function
\(\rightarrow ln(1.5) = 0.06t\) since \(ln(e^x) = x\)
\(\rightarrow \frac{ln(1.5)}{0.06} = t\) divide
\(\rightarrow t \approx 6.757751802\)
Thus, it would take about 6 years and 9 months.
If you deposit $1000 in an account paying 5% interest compounded monthly, how long will it take for your money to double?
First, recall the discrete compound interest formula from Section 8.3:
\(P(t) = P_{0}(1+\frac{r}{n})^{nt}\) (8)
In this case, \(P_{0} = 1000\), r = .05, and n = 12. Inserting these values into the formula, we obtain
\(P(t) = 1000(1+\frac{.05}{12})^{12t}\).
Now we want the future value P(t) of the account at some time t to equal twice the initial amount. In other words, we want P(t) to equal 2000. Therefore, we must solve the equation
\(2000 = 1000(1+\frac{.05}{12})^{12t}\).
Following the steps in Examples 2 and 3,
\(2000 = 1000(1+\frac{.05}{12})^{12t}\)
\(\rightarrow 2 = (1+\frac{.05}{12})^{12t}\) isolate the exponential
\(\rightarrow log(2) = log((1+\frac{.05}{12})^{12t})\) apply the common log function
\(\rightarrow log(2) = 12tlog(1+\frac{.05}{12})\) use property (c)
\(\rightarrow \frac{log(2)}{12log(1+\frac{.05}{12})} = t\) divide
\(\rightarrow t \approx 13.89180573\)
Thus, it would take about 13.9 years for your money to double.
Exercise
In Exercises 1-10, use a calculator to evaluate the function at the given value p. Round your answer to the nearest hundredth.
\(f(x) = log_{4}(x)\); p = 57.60.
- Answer
-
2.92
\(f(x) = log_{4}(x)\); p = 11.22.
\(f(x) = log_{7}(x)\); p = 2.98.
- Answer
-
0.56
\(f(x) = log_{3}(x)\); p = 2.27.
\(f(x) = log_{6}(x)\); p = 2.56.
- Answer
-
0.52
\(f(x) = log_{8}(x)\); p = 289.27.
\(f(x) = log_{8}(x)\); p = 302.67.
- Answer
-
2.75
\(f(x) = log_{5}(x)\); p = 15.70.
\(f(x) = log_{8}(x)\); p = 46.13.
- Answer
-
1.84
\(f(x) = log_{4}(x)\); p = 15.59.
In Exercises 11-18, perform each of the following tasks.
- Approximate the solution of the given equation using your graphing calculator. Load each side of the equation into the Y= menu of your calculator. Adjust the WINDOW parameters so that the point of intersection of the graphs is visible in the viewing window. Use the intersect utility in the CALC menu of your calculator to determine the x-coordinate of the point of intersection. Then make an accurate copy of the image in your viewing window on your homework paper.
- Solve the given equation algebraically, and round your answer to the nearest hundredth.
\(20 = 3(1.2)^x\)
- Answer
-
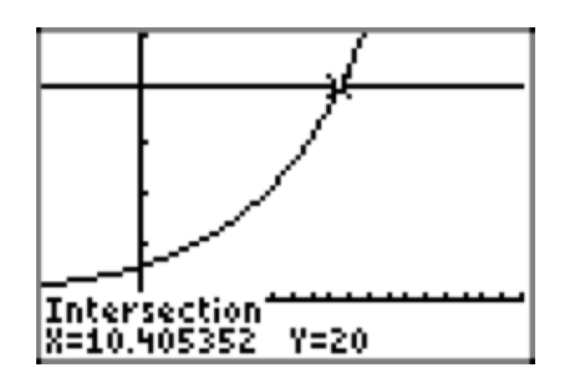
- 10.41
\(15 = 2(1.8)^x\)
\(14 = (1.4)^{5x}\)
- Answer
-
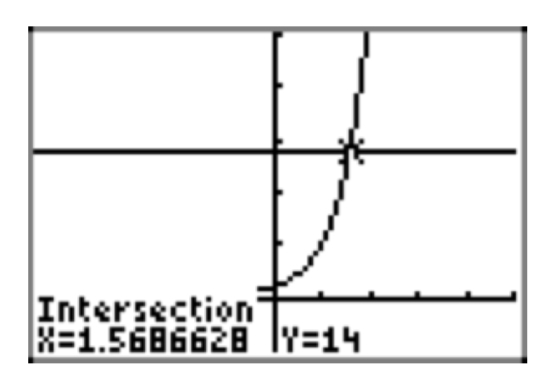
- 1.57
\(16 = (1.8)^{4x}\)
\(−4 = 0.2^x−9\)
- Answer
-
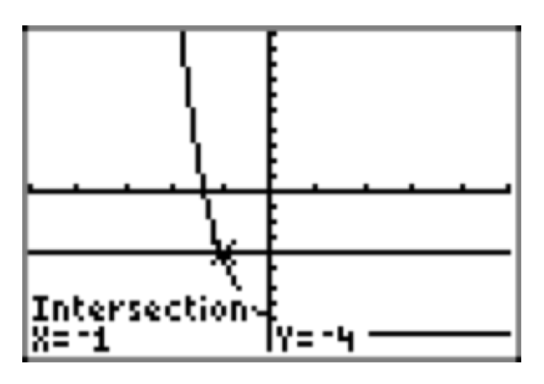
- −1.00
\(12 = 2.9^x+2\)
\(13 = 0.1^{x+1}\)
- Answer
-
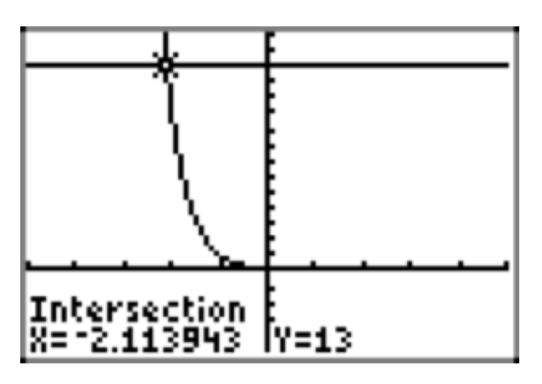
- −2.11
\(19 = 1.2^{x−6}\)
In Exercises 19-34, solve the given equation algebraically, and round your answer to the nearest hundredth.
\(20 = e^{x−3}\)
- Answer
-
6.00
\(−4 = e^x−9\)
\(23 = 0.9^x+9\)
- Answer
-
−25.05
\(10 = e^x+7\)
\(19 = e^x+5\)
- Answer
-
2.64
\(4 = 7(2.3)^x\)
\(18 = e^{x+4}\)
- Answer
-
−1.11
\(15 = e^{x+6}\)
\(8 = 2.7^{3x}\)
- Answer
-
0.70
\(7 = e^x+1\)
\(7 = 1.1^{8x}\)
- Answer
-
2.55
\(6 = 0.2^{x−8}\)
\(−7 = 1.3^{x−9}\)
- Answer
-
2.64
\(11 = 3(0.7)^x\)
\(23 = e^x+9\)
- Answer
-
2.64
\(20 = 3.2^{x+1}\)
Suppose that you invest $17,000 at 6% interest compounded daily. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
- Answer
-
11.55 years
Suppose that you invest $6,000 at 9% interest compounded continuously. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
Suppose that you invest $16,000 at 6% interest compounded daily. How many years will it take for your investment to reach $26,000? Round your answer to the nearest hundredth.
- Answer
-
8.09 years
Suppose that you invest $15,000 at 5% interest compounded monthly. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
Suppose that you invest $18,000 at 3% interest compounded monthly. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
- Answer
-
23.13 years
Suppose that you invest $7,000 at 5% interest compounded daily. How many years will it take for your investment to reach $13,000? Round your answer to the nearest hundredth.
Suppose that you invest $16,000 at 9% interest compounded continuously. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
- Answer
-
7.70 years
Suppose that you invest $16,000 at 2% interest compounded continuously. How many years will it take for your investment to reach $25,000? Round your answer to the nearest hundredth.
Suppose that you invest $2,000 at 5% interest compounded continuously. How many years will it take for your investment to reach $10,000? Round your answer to the nearest hundredth.
- Answer
-
32.19 years
Suppose that you invest $4,000 at 6% interest compounded continuously. How many years will it take for your investment to reach $10,000? Round your answer to the nearest hundredth.
Suppose that you invest $4,000 at 3% interest compounded daily. How many years will it take for your investment to reach $14,000? Round your answer to the nearest hundredth.
- Answer
-
41.76 years
Suppose that you invest $13,000 at 2% interest compounded monthly. How many years will it take for your investment to reach $20,000? Round your answer to the nearest hundredth.
Suppose that you invest $20,000 at 7% interest compounded continuously. How many years will it take for your investment to reach $30,000? Round your answer to the nearest hundredth.
- Answer
-
5.79 years
Suppose that you invest $16,000 at 4% interest compounded continuously. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
Suppose that you invest $8,000 at 8% interest compounded continuously. How many years will it take for your investment to double? Round your answer to the nearest hundredth.
- Answer
-
8.66 years
Suppose that you invest $3,000 at 3% interest compounded daily. How many years will it take for your investment to double? Round your answer to the nearest hundredth.


