8.7: Exponential Growth and Decay
- Page ID
- 23265
Exponential Growth Models
Recalling the investigations in Section 8.3, we started by developing a formula for discrete compound interest. This led to another formula for continuous compound interest,
\(P(t) = P_{0}e^{rt}\), (1)
where \(P_{0}\) is the initial amount (principal) and r is the annual interest rate in decimal form. If money in a bank account grows at an annual rate r (via payment of interest), and if the growth is continually added in to the account (i.e., interest is continuously compounded), then the balance in the account at time t years is P(t), as given by formula (1).
But we can use the exact same analysis for quantities other than money. If P(t) represents the amount of some quantity at time t years, and if P(t) grows at an annual rate r with the growth continually added in, then we can conclude in the same manner that P(t) must have the form
\(P(t) = P_{0}e^{rt}\), (2)
where \(P_{0}\) is the initial amount at time t = 0, namely P(0).
A classic example is uninhibited population growth. If a population P (t) of a certain species is placed in a good environment, with plenty of nutrients and space to grow, then it will grow according to formula (2). For example, the size of a bacterial culture in a petri dish will follow this formula very closely if it is provided with optimal living conditions. Many other species of animals and plants will also exhibit this behavior if placed in an environment in which they have no predators. For example, when the British imported rabbits into Australia in the late 18th century for hunting, the rabbit population exploded because conditions were good for living and reproducing, and there were no natural predators of the rabbits.
If a function P(t) grows continually at a rate r > 0, then P (t) has the form
\(P(t) = P_{0}e^{rt}\), (3)
where \(P_{0}\) is the initial amount P(0). In this case, the quantity P(t) is said to exhibit exponential growth, and r is the growth rate.
Remarks 4.
- If a physical quantity (such as population) grows according to formula (3), we say that the quantity is modeled by the exponential growth function P(t).
- Some may argue that population growth of rabbits, or even bacteria, is not really continuous. After all, rabbits are born one at a time, so the population actually grows in discrete chunks. This is certainly true, but if the population is large, then the growth will appear to be continuous. For example, consider the world population of humans. There are so many people in the world that there are many new births and deaths each second. Thus, the time difference between each 1 unit change in the population is just a tiny fraction of a second, and consequently the discrete growth will act virtually the same as continuous growth. (This is analogous to the almost identical results for continuous compounding and discrete daily compounding that we found in Section 8.3; compounding each second or millisecond would be even closer.)
- Likewise, using the continuous exponential growth formula (3) to model discrete quantities will sometimes result in fractional answers. In this case, the results will need to be rounded off in order to make sense. For example, an answer of 224.57 rabbits is not actually possible, so the answer should be rounded to 225.
- In formula (3), if time is measured in years (as we have done so far in this chapter), then r is the annual growth rate. However, time can instead be measured in any convenient units. The same formula applies, except that the growth rate r is given in terms of the particular time units used. For example, if time t is measured in hours, then r is the hourly growth rate.
In Section 8.2, we showed that a function of the form bt with b > 1 is an exponential
growth function. Likewise, if A > 0, then the more general exponential function \(Ab^t\) also exhibits exponential growth, since the graph of \(Ab^t\) is just a vertical scaling of the graph of \(b^t\). However, the exponential growth function in formula (3) appears to be different. We will show below that the function \(P_{0}e^{rt}\) can in fact be written in the form \(Ab^t\) with b > 1.
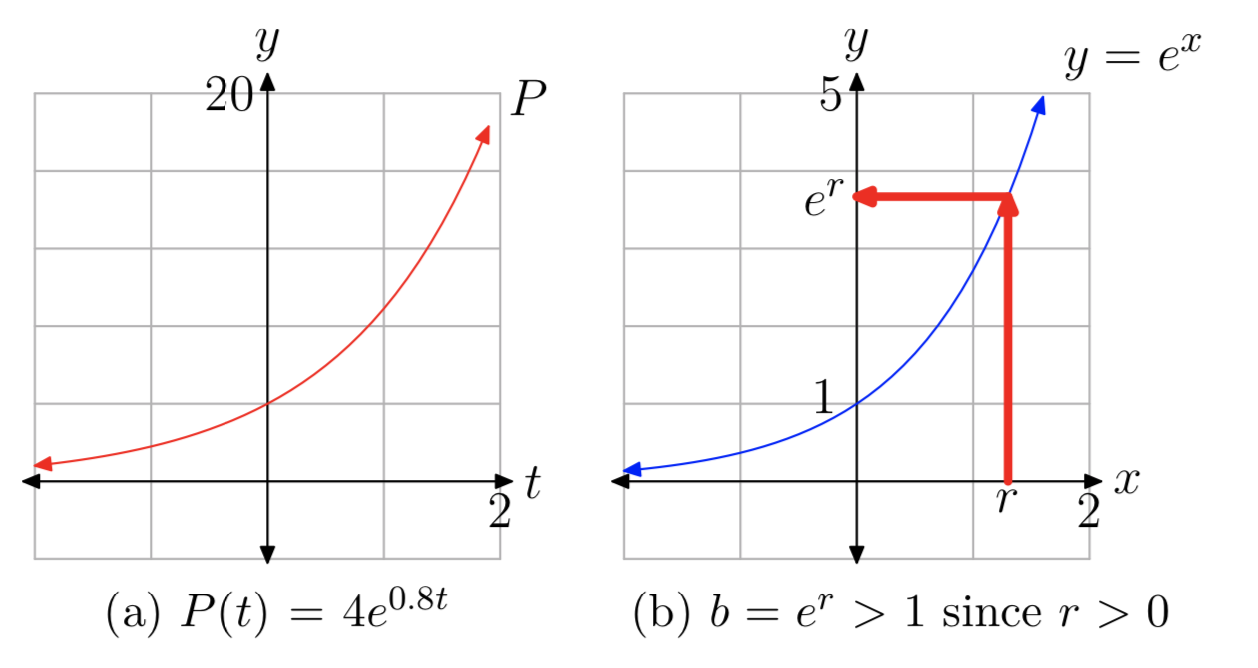
Let’s first look at a specific example. Suppose \(P(t) = 4e^{0.8t}\). Using the Laws of Exponents, we can rewrite P(t) as
\(P(t) = 4e^{0.8t} = 4(e^{0.8})^t\). (5)
Since \(e^{0.8} \approx 2.22554\), it follows that
\(P(t) ≈ 4(2.22554)^t\).
Because the base \(\approx 2.22554\) is larger than 1, this shows that P(t) is an exponential growth function, as seen in Figure 1(a)).
Now suppose that P(t) is any function of the form \(P_{0}e^{rt}\) with r > 0. As in (5) above, we can use the Laws of Exponents to rewrite P(t) as
\(P(t) = P_{0}e^{rt} = P_{0}(e^{r})^t = P_{0}b^t\) with \(b = e^r\).
To prove that b > 1, consider the graph of \(y = e^x\) shown in Figure 1(b). Recall that \(e \approx 2.718\), so e > 1, and therefore \(y = e^x\) is itself an exponential growth curve. Also, the y-intercept is (0,1) since \(e^0 = 1\). It follows that \(b = e^r > 1\) since r > 0 (see Figure 1(b)).
Therefore, functions of the form \(P(t) = P_{0}e^{rt}\) with r > 0 are exponential growth functions.
Applications of Exponential Growth
We will now examine the role of exponential growth functions in some real-world applications. In the following examples, assume that the population is modeled by an exponential growth function as in formula (3).
Suppose that the population of a certain country grows at an annual rate of 2%. If the current population is 3 million, what will the population be in 10 years?
This is a future value problem. If we measure population in millions and time in years, then \(P(t) = P_{0}e^{rt}\) with \(P_{0} = 3\) and r = 0.02. Inserting these particular values into formula (3), we obtain
\(P(t) = 3e^{0.02t}\).
The population in 10 years is \(P(10) = 3e^{(0.02)(10)} \approx 3.664208\) million.
In the same country as in Example 6, how long will it take the population to reach 5 million?
As before,
\(P(t) = 3e^{0.02t}\).
Now we want to know when the future value P(t) of the population at some time t will equal 5 million. Therefore, we need to solve the equation P(t) = 5 for time t, which leads to the exponential equation
\(5 = 3e^{0.02t}\).
Using the procedure for solving exponential equations that was presented in Section8.6,
\(5 = 3e^{0.02t}\).
\(\rightarrow \frac{5}{3} = e^{0.02t}\) isolate the exponential
\(\rightarrow ln(\frac{5}{3}) = ln(e^{0.02t})\) apply the natural log function
\(\rightarrow ln(\frac{5}{3}) = 0.02t\) since \(ln(e^x) = x\)
\(\rightarrow \frac{ln(\frac{5}{3})}{0.02} = t\) divide
\(\rightarrow t \approx 25.54128\)
Thus, it would take about 25.54 years for the population to reach 5 million.
The population of bacteria is typically measured by weight, as in the next two examples.
Suppose that a size of a bacterial culture is given by the function
\(P(t) = 100e^{0.15t}\),
where the size P(t) is measured in grams and time t is measured in hours. How long will it take for the culture to double in size?
The initial size is \(P_{0} = 100\) grams, so we want to know when the future value P(t) at some time t will equal 200. Therefore, we need to solve the equation P(t) = 200 for time t, which leads to the exponential equation
\(200 = 100e^{0.15t}\).
Using the same procedure as in the last example,
\(200 = 100e^{0.15t}\)
\(\rightarrow 2 = e^{0.15t}\) isolate the exponential
\(\rightarrow ln(2) = ln(e^{0.15t})\) apply the natural log function
\(\rightarrow ln(2) = 0.15t\) since \(ln(e^x) = x\)
\(\rightarrow \frac{ln(2)}{0.15} = t\) division
\(\rightarrow t \approx 4.620981\).
Thus, it would take about 4.62 hours for the size to double.
The last example deserves an additional comment. Suppose that we had started with 1000 grams instead of 100. Then to double in size would require a future value of 2000 grams. Therefore, in this case, we would have to solve the equation
\(2000 = 1000e^{0.15t}\).
But the first step is to isolate the exponential by dividing both sides by 1000 to get
\(2 = e^{0.15t}\),
and this is the same as the second line of the solution in the last example, so the answer will be the same. Likewise, repeating this argument for any initial amount will lead to the same second line, and therefore the same answer. Thus, the doubling time depends only on r, not on the initial amount \(P_{0}\).
Exponential Decay Models
We’ve observed that if a quantity increases continually at a rate r, then it is modeled by a function of the form \(P(t) = P_{0}e^{rt}\). But what if a quantity decreases instead? Although we won’t present the details here, the analysis can be carried out in the same way as the derivation of the continuous compounding formula in Section 8.3. The only difference is that the growth rate r in the formulas must be replaced by −r since the quantity is decreasing. The conclusion is that the quantity is modeled by a function of the form \(P(t) = P_{0}e^{−rt}\) instead of \(P_{0}e^{rt}\).
If a function P(t) decreases continually at a rate r > 0, then P(t) has the form
\(P(t) = P_{0}e^{−rt}\), (9)
where \(P_{0}\) is the initial amount P(0). In this case, the quantity P(t) is said to exhibit exponential decay, and r is the decay rate.
In Section 8.2, we showed that a function of the form bt with b < 1 is an exponential decay function. Likewise, if A > 0, then the more general exponential function \(Ab^t\) also exhibits exponential decay, since the graph of \(Ab^t\) is just a vertical scaling of the graph of bt. However, the exponential decay function in formula (9) appears to be different. We will show below that the function \(P_{0}e^{−rt}\) can in fact be written in the form \(Ab^t\) with b < 1.
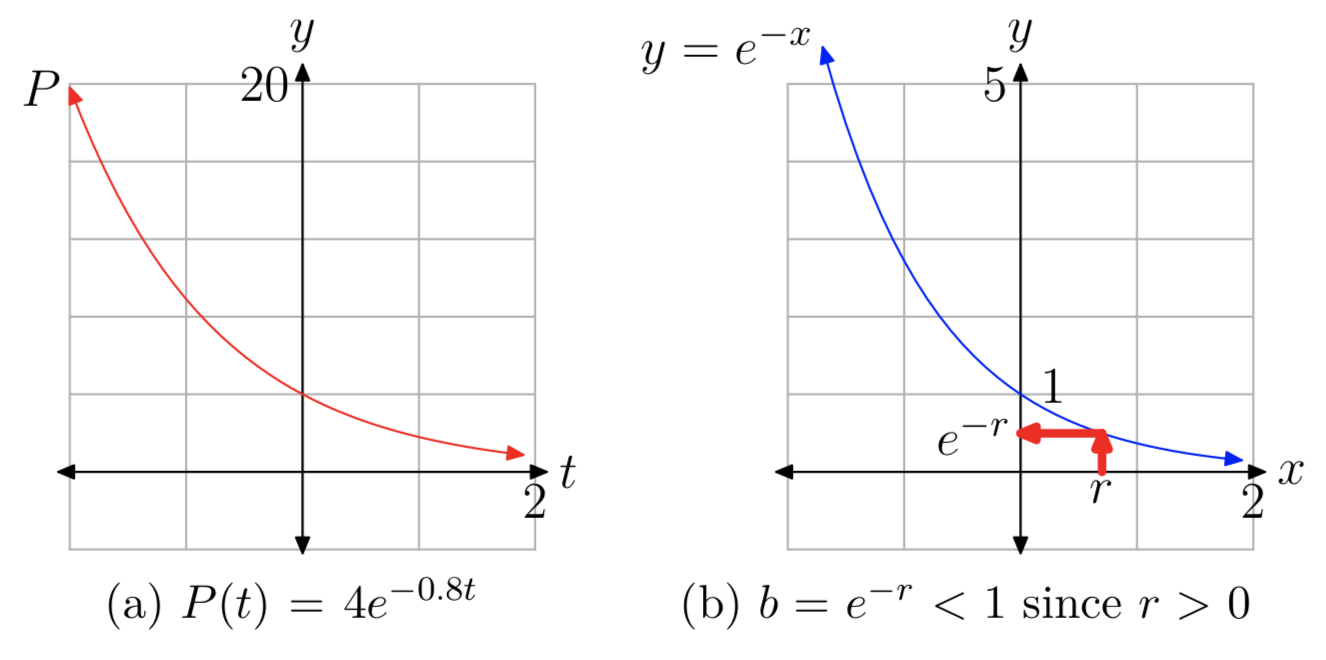
Let’s first look at a specific example. Suppose \(P(t) = 4e^{−0.8t}\). Using the Laws of Exponents, we can rewrite P(t) as
\(P(t) = 4e^{−0.8t} = 4(e^{−0.8})^t\). (10)
Since \(e^{−0.8} \approx 0.44933\), it follows that
\(P(t) \approx 4(0.44933)^t\).
Because the base \(\approx 0.44933\) is less than 1, this shows that P(t) is an exponential decay function, as seen in Figure 2(a)).
Now suppose that P(t) is any function of the form \(P_{0}e^{−rt}\) with r > 0. As in (10) above, we can use the Laws of Exponents to rewrite P(t) as
\(P(t) = P_{0}e^{−rt} = P_{0}(e^{−r})^t = P_{0}b^t\) with \(b = e^{−r}\).
To prove that b < 1, consider the graph of \(y = e^{−x}\) shown in Figure 2(b). Now
\(e^{−x} = (e^{−1})^x =(\frac{1}{e})^x\)
and \(\frac{1}{e} \approx 0.36788 < 1\), so \(y = e^{−x}\) is itself an exponential decay curve. (Alternatively, you can observe that the graph of \(y = e^{−x}\) is the reflection of the graph of \(y = e^x\) across the y-axis.) Also, the y-intercept is (0,1) since \(e^{−0} = 1\). It follows that \(b = e^{−r} < 1\) since r > 0 (see Figure 2(b)).
Therefore, functions of the form \(P(t) = P_{0}e^{−rt}\) with r > 0 are exponential decay functions.
Applications of Exponential Decay
The main example of exponential decay is radioactive decay. Radioactive elements and isotopes spontaneously emit subatomic particles, and this process gradually changes the substance into a different isotope. For example, the radioactive isotope Uranium-238 eventually decays into the stable isotope Lead-206. This is a random process for individual atoms, but overall the mass of the substance decreases according to the exponential decay formula (9).
Suppose that a certain radioactive element has an annual decay rate of 10%. Starting with a 200 gram sample of the element, how many grams will be left in 3 years?
This is a future value problem. If we measuring size in grams and time in years, then \(P(t) = P_{0}e^{−rt}\) with \(P_{0} = 200\) and r = 0.10. Inserting these particular values into formula (9), we obtain
\(P(t) = 200e^{−0.10t}\).
The amount in 3 years is \(P(3) = 200e^{−(0.10)(3)} \approx 148.1636\) grams.
Using the same element as in Example 11, if a particular sample of the element decays to 50 grams after 5 years, how big was the original sample?
This is a present value problem, where the unknown is the initial amount \(P_{0}\). As before, r = 0.10, so
\(P(t) = P_{0}e^{−0.10t}\).
Since P(5) = 50, we have the equation
\(50 = P(5) = P_{0}e^{−(0.10)(5)}\).
This equation can be solved by division:
\(\frac{50}{e^{−(0.10)(5)}} = P_{0}\)
Finish by calculating the value of the left side to get \(P_{0} \approx 82.43606\) grams.
Suppose that a certain radioactive isotope has an annual decay rate of 5%. How many years will it take for a 100 gram sample to decay to 40 grams?
Use \(P(t) = P_{0}e^{−rt}\) with \(P_{0} = 100\) and r = 0.05, so \(P(t) = 100e^{−0.05t}\).
Now we want to know when the future value P(t) of the size of the sample at some time t will equal 40. Therefore, we need to solve the equation P(t) = 40 for time t, which leads to the exponential equation
\(40 = 100e^{−0.05t}\).
Using the procedure for solving exponential equations that was presented in Section 8.6,
\(40 = 100e^{−0.05t}\)
\(\rightarrow 0.4 = e^{−0.05t}\) isolate the exponential
\(\rightarrow ln(0.4) = ln(e^{−0.05t})\) apply the natural log function
\(\rightarrow ln(0.4) = −0.05t\) since \(ln(e^x) = x\)
\(\rightarrow \frac{ln(0.4)}{−0.05} = t\) division
\(\rightarrow t \approx 18.32581\).
Thus, it would take approximately 18.33 years for the sample to decay to 40 grams.
We saw earlier that exponential growth processes have a fixed doubling time. Similarly, exponential decay processes have a fixed half-life, the time in which one-half the original amount decays.
Using the same element as in Example 13, what is the half-life of the element?
As before, r = 0.05, so
\(P(t) = P_{0}e^{−0.05t}\).
The initial size is \(P_{0}\) grams, so we want to know when the future value P(t) at some time t will equal one-half the initial amount, \(\frac{P_{0}}{2}\). Therefore, we need to solve the equation \(P(t) = \frac{P_{0}}{2}\) for time t, which leads to the exponential equation
\(\frac{P_{0}}{2} = P_{0}e^{−0.05t}\).
Using the same procedure as in the last example,
\(\frac{P_{0}}{2} = P_{0}e^{−0.05t}\)
\(\rightarrow \frac{1}{2} = e^{−0.05t}\) isolate the exponential
\(\rightarrow ln(\frac{1}{2}) = ln(e^{−0.05t})\) apply the natural log function
\(\rightarrow ln(\frac{1}{2}) = −0.05t\) since \(ln(e^x) = x\)
\(\rightarrow \frac{ln(\frac{1}{2})}{−0.05} = t\) division
\(\rightarrow t \approx 13.86294\)
Thus, the half-life is approximately 13.86 years.
The process of radioactive decay also forms the basis of the carbon-14 dating technique. The Earth’s atmosphere contains a tiny amount of the radioactive isotope carbon-14, and therefore plants and animals also contain some carbon-14 due to their interaction with the atmosphere. However, this interaction ends when a plant or animal dies, so the carbon-14 begins to decay (the decay rate is 0.012%). By comparing the amount of carbon-14 in a bone, for example, with the normal amount in a living animal, scientists can compute the age of the bone.
Suppose that only 1.5% of the normal amount of carbon-14 remains in a fragment of bone. How old is the bone?
Use \(P(t) = P_{0}e^{−rt}\) with r = 0.00012, so
\(P(t) = P_{0}e^{−0.00012t}\).
The initial size is \(P_{0}\) grams, so we want to know when the future value P(t) at some time t will equal 1.5% of the initial amount, \(0.015P_{0}\). Therefore, we need to solve the equation \(P(t) = 0.015P_{0}\) for time t, which leads to the exponential equation
\(0.015P_{0} = P_{0}e^{−0.00012t}\).
Using the same procedure as in Example 14,
\(0.015P_{0} = P_{0}e^{−0.00012t}\)
\(\rightarrow 0.015 = e^{−0.00012t}\) isolate the exponential
\(\rightarrow ln(0.015) = ln(e^{−0.00012t})\) apply the natural log function
\(\rightarrow ln(0.015) = −0.00012t\) since \(ln(e^x) = x\)
\(\rightarrow \frac{ln(0.015)}{−0.00012} = t\) division
\(\rightarrow t \approx 34998\)
Thus, the bone is approximately 34998 years old.
While the carbon-14 technique only works on plants and animals, there are other similar dating techniques, using other radioactive isotopes, that are used to date rocks and other inorganic matter.
Exercise
Suppose that the population of a certain town grows at an annual rate of 6%. If the population is currently 5, 000, what will it be in 7 years? Round your answer to the nearest integer.
- Answer
-
7610 people
Suppose that the population of a certain town grows at an annual rate of 5%. If the population is currently 2,000, how many years will it take for it to double? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 7.2%. How many years will it take for a 227 gram sample to decay to 93 grams? Round your answer to the nearest hundredth.
- Answer
-
12.39 yrs
Suppose that a certain radioactive isotope has an annual decay rate of 6.8%. How many years will it take for a 399 gram sample to decay to 157 grams? Round your answer to the nearest hundredth.
Suppose that the population of a certain town grows at an annual rate of 8%. If the population is currently 4,000, how many years will it take for it to double? Round your answer to the nearest hundredth.
- Answer
-
8.66 yrs
Suppose that a certain radioactive isotope has an annual decay rate of 19.2%. Starting with a 443 gram sample, how many grams will be left after 9 years? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 17.4%. What is the half-life (in years) of the isotope? Round your answer to the nearest hundredth.
- Answer
-
3.98 yrs
Suppose that the population of a certain town grows at an annual rate of 7%. If the population is currently 8,000, how many years will it take for it to reach 18,000? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 17.3%. Starting with a 214 gram sample, how many grams will be left after 5 years? Round your answer to the nearest hundredth.
- Answer
-
90.11g
Suppose that the population of a certain town grows at an annual rate of 7%. If the population grows to 2, 000 in 7 years, what was the original population? Round your answer to the nearest integer.
Suppose that the population of a certain town grows at an annual rate of 3%. If the population is currently 3,000, how many years will it take for it to double? Round your answer to the nearest hundredth.
- Answer
-
23.10 yrs
Suppose that a certain radioactive isotope has an annual decay rate of 12.5%. Starting with a 127 gram sample, how many grams will be left after 6 years? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 13.1%. Suppose that a certain radioactive isotope has an annual decay rate of 13.1%
- Answer
-
141.10g
Suppose that the population of a certain town grows at an annual rate of 2%. If the population grows to 9, 000 in 4 years, what was the original population? Round your answer to the nearest integer.
Suppose that the population of a certain town grows at an annual rate of 2%. If the population is currently 7,000, how many years will it take for it to double? Round your answer to the nearest hundredth.
- Answer
-
34.66 yrs
Suppose that a certain radioactive isotope has an annual decay rate of 5.3%. How many years will it take for a 217 gram sample to decay to 84 grams? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 18.7%. How many years will it take for a 324 gram sample to decay to 163 grams? Round your answer to the nearest hundredth.
- Answer
-
3.67 yrs
Suppose that the population of a certain town grows at an annual rate of 8%. If the population is currently 8,000, how many years will it take for it to reach 18,000? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 2.3%. If a particular sample decays to 25 grams after 8 years, how big (in grams) was the original sample? Round your answer to the nearest hundredth.
- Answer
-
30.05g
Suppose that the population of a certain town grows at an annual rate of 4%. If the population is currently 7,000, how many years will it take for it to reach 17,000? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 9.8%. If a particular sample decays to 11 grams after 6 years, how big (in grams) was the original sample? Round your answer to the nearest hundredth.
- Answer
-
19.80g
Suppose that the population of a certain town grows at an annual rate of 5%. If the population grows to 6, 000 in 3 years, what was the original population? Round your answer to the nearest integer.
Suppose that the population of a certain town grows at an annual rate of 8%. If the population is currently 6, 000, what will it be in 5 years? Round your answer to the nearest integer.
- Answer
-
8, 951 people
Suppose that a certain radioactive isotope has an annual decay rate of 15.8%. What is the half-life (in years) of the isotope? Round your answer to the nearest hundredth.
Suppose that the population of a certain town grows at an annual rate of 9%. If the population grows to 7, 000 in 5 years, what was the original population? Round your answer to the nearest integer.
- Answer
-
8, 951 people
Suppose that a certain radioactive isotope has an annual decay rate of 18.6%. If a particular sample decays to 41 grams after 3 years, how big (in grams) was the original sample? Round your answer to the nearest hundredth.
Suppose that a certain radioactive isotope has an annual decay rate of 5.2%. What is the half-life (in years) of the isotope? Round your answer to the nearest hundredth.
- Answer
-
13.33 yrs
Suppose that a certain radioactive isotope has an annual decay rate of 6.5%. What is the half-life (in years) of the isotope? Round your answer to the nearest hundredth.
Suppose that the population of a certain town grows at an annual rate of 8%. If the population is currently 2,000, how many years will it take for it to reach 7,000? Round your answer to the nearest hundredth.
- Answer
-
15.66 yrs
Suppose that a certain radioactive isotope has an annual decay rate of 3.7%. If a particular sample decays to 47 grams after 8 years, how big (in grams) was the original sample? Round your answer to the nearest hundredth.
Suppose that the population of a certain town grows at an annual rate of 6%. If the population is currently 7, 000, what will it be in 7 years? Round your answer to the nearest integer.
- Answer
-
10, 654 people
Suppose that the population of a certain town grows at an annual rate of 4%. If the population is currently 1, 000, what will it be in 3 years? Round your answer to the nearest integer.
In Exercises 33-40, use the fact that the decay rate of carbon-14 is 0.012%. Round your answer to the nearest year.
Suppose that only 8.6% of the normal amount of carbon-14 remains in a fragment of bone. How old is the bone?
- Answer
-
20445 years
Suppose that only 5.2% of the normal amount of carbon-14 remains in a fragment of bone. How old is the bone?
Suppose that 90.1% of the normal amount of carbon-14 remains in a piece of wood. How old is the wood?
- Answer
-
869 years
Suppose that 83.6% of the normal amount of carbon-14 remains in a piece of cloth. How old is the cloth?
Suppose that only 6.2% of the normal amount of carbon-14 remains in a fragment of bone. How old is the bone?
- Answer
-
23172 years
Suppose that only 1.3% of the normal amount of carbon-14 remains in a fragment of bone. How old is the bone?
Suppose that 96.7% of the normal amount of carbon-14 remains in a piece of cloth. How old is the cloth?
- Answer
-
280 years
Suppose that 84.9% of the normal amount of carbon-14 remains in a piece of wood. How old is the wood?

