Skip to main content
Mathematics LibreTexts

3.3E: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    30302

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Practice Makes Perfect

    Find the Slope of a Line

    In the following exercises, find the slope of each line shown.

    1.
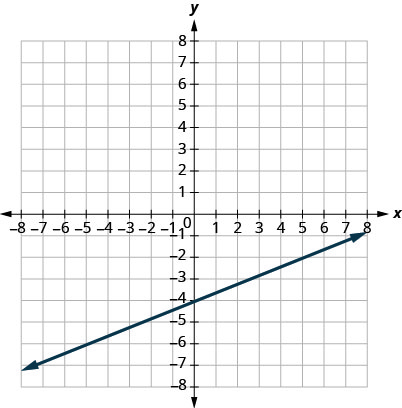
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, negative 4) and (5, negative 2).

    Answer

    \(m=\frac{2}{5}\)

    2.
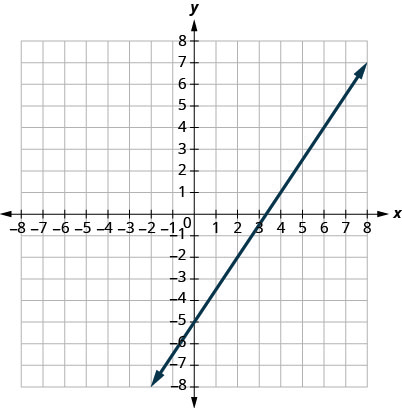
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, negative 5) and (2, negative 2).

    3.
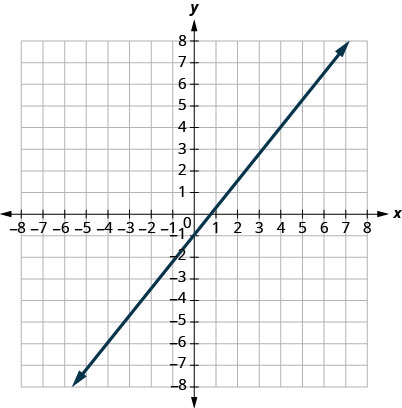
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, negative 1) and (4, 4).

    Answer

    \(m=\frac{5}{4}\)

    4.
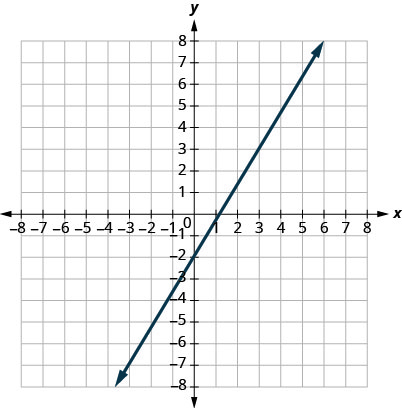
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, negative 2) and (3, 3).

    5.
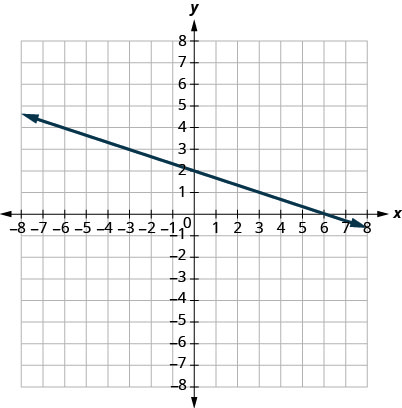
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, 2) and (3, 1).

    Answer

    \(m = -\frac{1}{3}\)

    6.
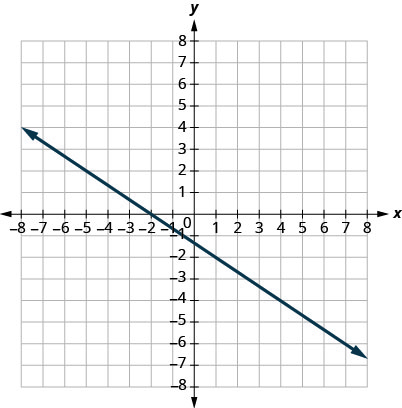
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, negative 1) and (3, negative 3).

    7.
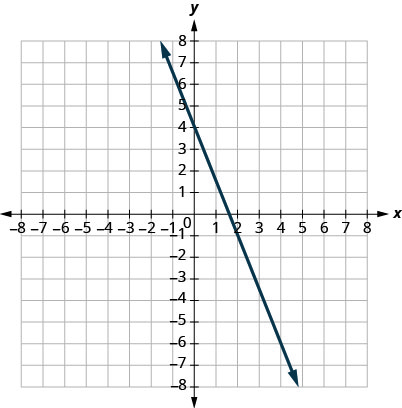
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, 4) and (2, negative 1).

    Answer

    \(m = -\frac{5}{2}\)

    8.
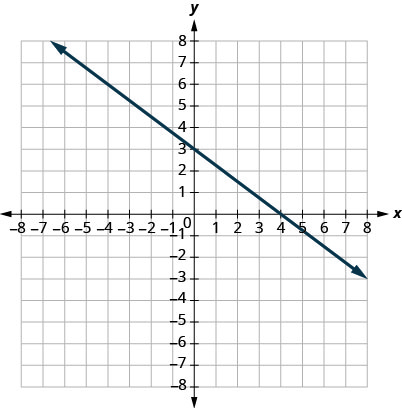
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, 2) and (4, negative 1).

    In the following exercises, find the slope of each line.

    9. \(y=3\)

    Answer

    \(m = 0\)

    10. \(y=−2\)

    11. \(x=−5\)

    Answer

    undefined

    12. \(x=4\)

    In the following exercises, use the slope formula to find the slope of the line between each pair of points.

    13. \((2,5),\;(4,0)\)

    Answer

    \(m = -\frac{5}{2}\)

    14. \((3,6),\;(8,0)\)

    15. \((−3,3),\;(4,−5)\)

    Answer

    \(m = -\frac{8}{7}\)

    16. \((−2,4),\;(3,−1)\)

    17. \((−1,−2),\;(2,5)\)

    Answer

    \(m = \frac{7}{3}\)

    18. \((−2,−1),\;(6,5)\)

    19. \((4,−5),\;(1,−2)\)

    Answer

    \(m = -1\)

    20. \((3,−6),\;(2,−2)\)

    Graph a Line Given a Point and the Slope

    In the following exercises, graph each line with the given point and slope.

    21. \((2,5)\); \(m=−\frac{1}{3}\)

    Answer

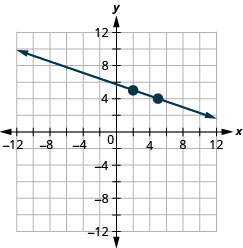
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 12 to 12. The y-axis runs from negative 12 to 12. The line goes through the points (2, 5) and (5, 4).

    22. \((1,4)\); \(m=−\frac{1}{2}\)

    23. \((−1,−4)\); \(m=\frac{4}{3}\)

    Answer

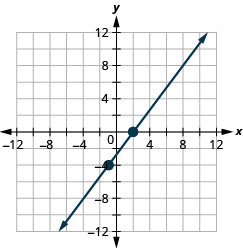
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 12 to 12. The y-axis runs from negative 12 to 12. The line goes through the points (negative 1, negative 4) and (2, 0).

    24. \((−3,−5)\); \(m=\frac{3}{2}\)

    25. \(y\)-intercept: \((0, 3)\); \(m=−\frac{2}{5}\)

    Answer

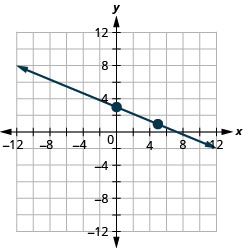
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 12 to 12. The y-axis runs from negative 12 to 12. The line goes through the points (0, 3) and (5, 1).

    26. \(x\)-intercept: \((−2,0)\); \(m=\frac{3}{4}\)

    27. \((−4,2)\); \(m=4\)

    Answer

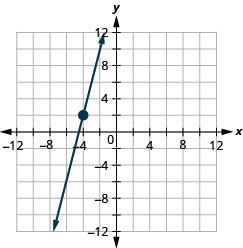
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 12 to 12. The y-axis runs from negative 12 to 12. The line goes through the points (negative 4, 2) and (negative 3, 6).

    28. \((1,5)\); \(m=−3\)

    Graph a Line Using Its Slope and Intercept

    In the following exercises, identify the slope and y-intercept of each line.

    29. \(y=−7x+3\)

    Answer

    \(m=−7\); \((0,3)\)

    30. \(y=4x−10\)

    31. \(3x+y=5\)

    Answer

    \(m=−3\); \((0,5)\)

    32. \(4x+y=8\)

    33. \(6x+4y=12\)

    Answer

    \(m=−\frac{3}{2}\); \((0,3)\)

    34. \(8x+3y=12\)

    35. \(5x−2y=6\)

    Answer

    \(m=\frac{5}{2}\); \((0,−3)\)

    36. \(7x−3y=9\)

    In the following exercises, graph the line of each equation using its slope and y-intercept.

    37. \(y=3x−1\)

    Answer

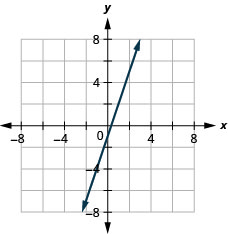
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 1) and (1, 2).

    38. \(y=2x−3\)

    39. \(y=−x+3\)

    Answer

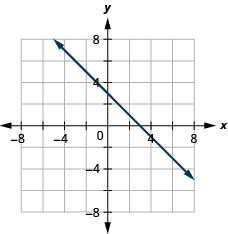
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, 3) and (1, 2).

    40. \(y=−x−4\)

    41. \(y=−\frac{2}{5}x−3\)

    Answer

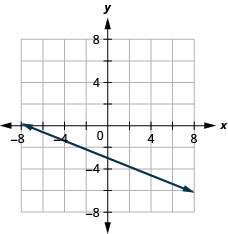
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 3) and (5, negative 5).

    42. \(y=−\frac{3}{5}x+2\)

    43. \(3x−2y=4\)

    Answer

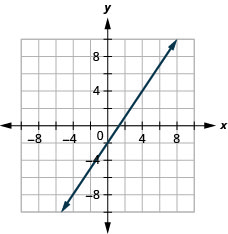
    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 2) and (2, 1).

    44. \(3x−4y=8\)

    Choose the Most Convenient Method to Graph a Line

    In the following exercises, determine the most convenient method to graph each line.

    45. \(x=2\)

    Answer

    vertical line

    46. \(y=5\)

    47. \(y=−3x+4\)

    Answer

    slope-intercept

    48. \(x−y=5\)

    49. \(x−y=1\)

    Answer

    intercepts

    50. \(y=\frac{2}{3}x−1\)

    51. \(3x−2y=−12\)

    Answer

    intercepts

    52. \(2x−5y=−10\)

    Graph and Interpret Applications of Slope–Intercept

    53. The equation \(P=31+1.75w\) models the relation between the amount of Tuyet’s monthly water bill payment, \(P\), in dollars, and the number of units of water, \(w\), used.

    a. Find Tuyet’s payment for a month when \(0\) units of water are used.

    b. Find Tuyet’s payment for a month when \(12\) units of water are used.

    c. Interpret the slope and \(P\)-intercept of the equation.

    d. Graph the equation.

    Answer

    a. \($31\)
    b. \($52\)
    c. The slope, \(1.75\), means that the payment, \(P\), increases by \($1.75\) when the number of units of water used, \(w\), increases by \(1\). The \(P\)-intercept means that when the number units of water Tuyet used is \(0\), the payment is \($31\).
    d.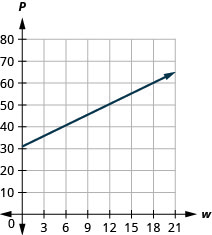

    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 1 to 21. The y-axis runs from negative 1 to 80. The line goes through the points (0, 31) and (12, 52).

    54. The equation \(P=28+2.54w\) models the relation between the amount of Randy’s monthly water bill payment, \(P\), in dollars, and the number of units of water, \(w\), used.

    a. Find the payment for a month when Randy used \(0\) units of water.

    b. Find the payment for a month when Randy used \(15\) units of water.

    c. Interpret the slope and \(P\)-intercept of the equation.

    d. Graph the equation.

    55. Bruce drives his car for his job. The equation \(R=0.575m+42\) models the relation between the amount in dollars, \(R\), that he is reimbursed and the number of miles, \(m\), he drives in one day.

    a. Find the amount Bruce is reimbursed on a day when he drives \(0\) miles.

    b. Find the amount Bruce is reimbursed on a day when he drives \(220\) miles.

    c. Interpret the slope and \(R\)-intercept of the equation.

    d. Graph the equation.

    Answer

    a. \($42\)
    b. \($168.50\)
    c. The slope, \(0.575\) means that the amount he is reimbursed, \(R\), increases by \($0.575\) when the number of miles driven, \(m\), increases by \(1\). The \(R\)-intercept means that when the number miles driven is \(0\), the amount reimbursed is \($42\).
    d.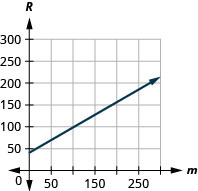

    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 50 to 250. The y-axis runs from negative 50 to 300. The line goes through the points (0, 42) and (220, 168.5).

    56. Janelle is planning to rent a car while on vacation. The equation \(C=0.32m+15\) models the relation between the cost in dollars, \(C\), per day and the number of miles, \(m\), she drives in one day.

    a. Find the cost if Janelle drives the car \(0\) miles one day.

    b. Find the cost on a day when Janelle drives the car \(400\) miles.

    c. Interpret the slope and \(C\)-intercept of the equation.

    d. Graph the equation.

    57. Cherie works in retail and her weekly salary includes commission for the amount she sells. The equation \(S=400+0.15c\) models the relation between her weekly salary, \(S\), in dollars and the amount of her sales, \(c\), in dollars.

    a. Find Cherie’s salary for a week when her sales were \($0\).

    b. Find Cherie’s salary for a week when her sales were \($3,600\).

    c. Interpret the slope and \(S\)-intercept of the equation.

    d. Graph the equation.

    Answer

    a. \($400\)
    b. \($940\)
    c. The slope, \(0.15\), means that Cherie’s salary, S, increases by \($0.15\) for every \($1\) increase in her sales. The \(S\)-intercept means that when her sales are \($0\), her salary is \($400\).
    d.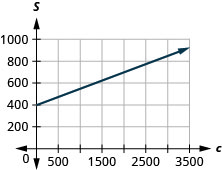

    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 500 to 3500. The y-axis runs from negative 200 to 1000. The line goes through the points (0, 400) and (3600, 940).

    58. Patel’s weekly salary includes a base pay plus commission on his sales. The equation \(S=750+0.09c\) models the relation between his weekly salary, \(S\), in dollars and the amount of his sales, \(c\), in dollars.

    a. Find Patel’s salary for a week when his sales were \(0\).

    b. Find Patel’s salary for a week when his sales were \(18,540\).

    c. Interpret the slope and \(S\)-intercept of the equation.

    d. Graph the equation.

    59. Costa is planning a lunch banquet. The equation \(C=450+28g\) models the relation between the cost in dollars, \(C\), of the banquet and the number of guests, \(g\).

    a. Find the cost if the number of guests is \(40\).

    b. Find the cost if the number of guests is \(80\).

    c. Interpret the slope and \(C\)-intercept of the equation.

    d. Graph the equation.

    Answer

    a. \($1570\)
    b. \($5690\)
    c. The slope gives the cost per guest. The slope, \(28\), means that the cost, \(C\), increases by \($28\) when the number of guests increases by \(1\). The \(C\)-intercept means that if the number of guests was \(0\), the cost would be \($450\).
    d.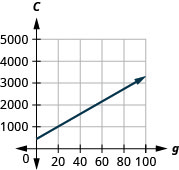

    This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 20 to 100. The y-axis runs from negative 1000 to 7000. The line goes through the points (0, 450) and (40, 1570).

    60. Margie is planning a dinner banquet. The equation \(C=750+42g\) models the relation between the cost in dollars, \(C\), of the banquet and the number of guests, \(g\).

    a. Find the cost if the number of guests is \(50\).

    b. Find the cost if the number of guests is \(100\).

    c. Interpret the slope and \(C\)-intercept of the equation.

    d. Graph the equation.

    Use Slopes to Identify Parallel and Perpendicular Lines

    In the following exercises, use slopes and \(y\)-intercepts to determine if the lines are parallel, perpendicular, or neither.

    61. \(y=\frac{3}{4}x−3\); \(3x−4y=−2\)

    Answer

    parallel

    62. \(3x−4y=−2\); \(y=\frac{3}{4}x−3\)

    63. \(2x−4y=6\); \(x−2y=3\)

    Answer

    neither

    64. \(8x+6y=6\); \(12x+9y=12\)

    65. \(x=5\); \(x=−6\)

    Answer

    parallel

    66. \(x=−3\); \(x=−2\)

    67. \(4x−2y=5\); \(3x+6y=8\)

    Answer

    perpendicular

    68. \(8x−2y=7\); \(3x+12y=9\)

    69. \(3x−6y=12\); \(6x−3y=3\)

    Answer

    neither

    70. \(9x−5y=4\); \(5x+9y=−1\)

    71. \(7x−4y=8\); \(4x+7y=14\)

    Answer

    perpendicular

    72. \(5x−2y=11\); \(5x−y=7\)

    73. \(3x−2y=8\); \(2x+3y=6\)

    Answer

    perpendicular

    74. \(2x+3y=5\); \(3x−2y=7\)

    75. \(3x−2y=1\); \(2x−3y=2\)

    Answer

    neither

    76. \(2x+4y=3\); \(6x+3y=2\)

    77. \(y=2\); \(y=6\)

    Answer

    parallel

    78. \(y=−1\); \(y=2\)

    Writing Exercises

    79. How does the graph of a line with slope \(m=12\) differ from the graph of a line with slope \(m=2\)?

    Answer

    Answers will vary.

    80. Why is the slope of a vertical line “undefined”?

    81. Explain how you can graph a line given a point and its slope.

    Answer

    Answers will vary.

    82. Explain in your own words how to decide which method to use to graph a line.

    Self Check

    a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

    This table has 7 rows and 4 columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is “Confidently”, the third is “With some help”, and the fourth is “No, I don’t get it”. Under the first column are the phrases “find the slope of a line”, “graph a line given a point and the slope”, “graph a line using its slope and intercept”, “choose the most convenient method to graph a line”, “graph and interpret applications of slope-intercept”, and “use slopes to identify parallel and perpendicular lines”. The other columns are left blank so that the learner may indicate their mastery level for each topic.

    b. After reviewing this checklist, what will you do to become confident for all objectives?

    This page titled 3.3E: Exercises is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      OpenStax
      License
      CC BY
      License Version
      4.0
      OER program or Publisher
      OpenStax
    2. Tags
      1. source@https://openstax.org/details/books/intermediate-algebra-2e