4.7E: Exercises
- Page ID
- 30312
Practice Makes Perfect
Evaluate the Determinant of a 2 × 2 Matrix
In the following exercises, evaluate the determinate of each square matrix.
\(\left[\begin{matrix}6&−2\\3&−1\end{matrix}\right]\)
\(\left[\begin{matrix}−4&8\\−3&5\end{matrix}\right]\)
- Answer
-
\(4\)
\(\left[\begin{matrix}−3&5\\0&−4\end{matrix}\right]\)
\(\left[\begin{matrix}−2&0\\7&−5\end{matrix}\right]\)
- Answer
-
\(10\)
Evaluate the Determinant of a 3 × 3 Matrix
In the following exercises, find and then evaluate the indicated minors.
\(\left|\begin{matrix}3&−1&4\\−1&0&−2\\−4&1&5\end{matrix}\right|\)
Find the minor ⓐ \(a_1\) ⓑ \(b_2\) ⓒ \(c_3\)
\(\left|\begin{matrix}−1&−3&2\\4&−2&−1\\−2&0&−3\end{matrix}\right|\)
Find the minor ⓐ \(a_1\) ⓑ \(b_1\) ⓒ \(c_2\)
- Answer
-
ⓐ 6 ⓑ \(−14\) ⓒ \(−6\)
\(\left|\begin{matrix}2&−3&−4\\−1&2&−3\\0&−1&−2\end{matrix}\right|\)
Find the minor ⓐ \(a_2\) ⓑ \(b_2\) ⓒ \(c_2\)
\(\left|\begin{matrix}−2&−2&3\\1&−3&0\\−2&3&−2\end{matrix}\right|\)
Find the minor ⓐ \(a_3\) ⓑ \(b_3\) ⓒ \(c_3\)
- Answer
-
ⓐ 9 ⓑ \(−3\) ⓒ 8
In the following exercises, evaluate each determinant by expanding by minors along the first row.
\(\left|\begin{matrix}−2&3&−1\\−1&2&−2\\3&1&−3\end{matrix}\right|\)
\(\left|\begin{matrix}4&−1&−2\\−3&−2&1\\−2&−5&7\end{matrix}\right|\)
- Answer
-
\(−77\)
\(\left|\begin{matrix}−2&−3&−4\\5&−6&7\\−1&2&0\end{matrix}\right|\)
\(\left|\begin{matrix}1&3&−2\\5&−6&4\\0&−2&−1\end{matrix}\right|\)
- Answer
-
\(49\)
In the following exercises, evaluate each determinant by expanding by minors.
\(\left|\begin{matrix}−5&−1&−4\\4&0&−3\\2&−2&6\end{matrix}\right|\)
\(\left|\begin{matrix}4&−1&3\\3&−2&2\\−1&0&4\end{matrix}\right|\)
- Answer
-
\(−24\)
\(\left|\begin{matrix}3&5&4\\−1&3&0\\−2&6&1\end{matrix}\right|\)
\(\left|\begin{matrix}2&−4&−3\\5&−1&−4\\3&2&0\end{matrix}\right|\)
- Answer
-
\(25\)
Use Cramer’s Rule to Solve Systems of Equations
In the following exercises, solve each system of equations using Cramer’s Rule.
\(\left\{\begin{array} {l} −2x+3y=3\\x+3y=12\end{array}\right.\)
\(\left\{\begin{array} {l} x−2y=−5\\2x−3y=−4\end{array}\right.\)
- Answer
-
\((7,6)\)
\(\left\{\begin{array} {l} x−3y=−9\\2x+5y=4\end{array}\right.\)
\(\left\{\begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.\)
- Answer
-
\((−2,0)\)
\(\left\{\begin{array} {l} x−2y=−5\\2x−3y=−4\end{array}\right.\)
\(\left\{\begin{array} {l} x−3y=−9\\2x+5y=4\end{array}\right.\)
- Answer
-
\((−3,2)\)
\(\left\{\begin{array} {l} 5x−3y=−1\\2x−y=2\end{array}\right.\)
\(\left\{\begin{array} {l} 3x+8y=−3\\2x+5y=−3\end{array}\right.\)
- Answer
-
\((−9,3)\)
\(\left\{\begin{array} {l} 6x−5y+2z=3\\2x+y−4z=5\\3x−3y+z=−1 \end{array}\right.\)
\(\left\{\begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7\end{array}\right.\)
- Answer
-
\((−3,−5,4)\)
\(\left\{\begin{array} {l} 2x−5y+3z=8\\3x−y+4z=7\\x+3y+2z=−3\end{array}\right.\)
\(\left\{\begin{array} {l} 11x+9y+2z=−9\\7x+5y+3z=−7\\4x+3y+z=−3\end{array}\right.\)
- Answer
-
\((2,−3,−2)\)
\(\left\{\begin{array} {l} x+2z=0\\4y+3z=−2\\2x−5y=3\end{array}\right.\)
\(\left\{\begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3\end{array}\right.\)
- Answer
-
\((−3,2,3)\)
\(\left\{\begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1\end{array}\right.\)
\(\left\{\begin{array} {l} 3x−z=−3\\5y+2z=−6\\4x+3y=−8\end{array}\right.\)
- Answer
-
\((−2,0,−3)\)
\(\left\{\begin{array} {l} 2x+y=3\\6x+3y=9\end{array}\right.\)
\(\left\{\begin{array} {l} x−4y=−1\\−3x+12y=3\end{array}\right.\)
- Answer
-
infinitely many solutions
\(\left\{\begin{array} {l} −3x−y=4\\6x+2y=−16\end{array}\right.\)
\(\left\{\begin{array} {l} 4x+3y=2\\20x+15y=5\end{array}\right.\)
- Answer
-
inconsistent
\(\left\{\begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1\end{array}\right.\)
\(\left\{\begin{array} {l} 2x+3y+z=1\\2x+y+z=9\\3x+4y+2z=20\end{array}\right.\)
- Answer
-
inconsistent
\(\left\{\begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6\end{array}\right.\)
\(\left\{\begin{array} {l} x−2y+3z=1\\x+y−3z=7\\3x−4y+5z=7\end{array}\right.\)
- Answer
-
infinitely many solutions
Solve Applications Using Determinants
In the following exercises, determine whether the given points are collinear.
\((0,1)\), \((2,0)\), and \((−2,2)\).
\((0,−5)\), \((−2,−2)\), and \((2,−8)\).
- Answer
-
yes
\((4,−3)\), \((6,−4)\), and \((2,−2)\).
\((−2,1)\), \((−4,4)\), and \((0,−2)\).
- Answer
-
no
Writing Exercises
Explain the difference between a square matrix and its determinant. Give an example of each.
Explain what is meant by the minor of an entry in a square matrix.
- Answer
-
Answers will vary.
Explain how to decide which row or column you will use to expand a \(3×3\) determinant.
Explain the steps for solving a system of equations using Cramer’s rule.
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
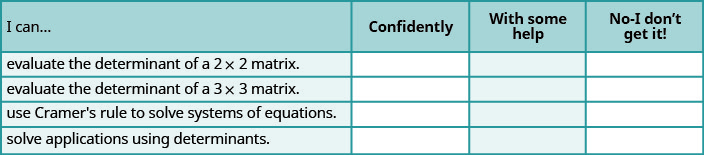
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?


