5.5E: Exercises
- Page ID
- 30317
Practice Makes Perfect
Divide Monomials
In the following exercises, divide the monomials.
1. \(15r^4s^9÷(15r^4s^9)\)
2. \(20m^8n^4÷(30m^5n^9)\)
- Answer
-
\(\dfrac{2m^3}{3n^5}\)
3. \(\dfrac{18a^4b^8}{−27a^9b^5}\)
4. \(\dfrac{45x^5y^9}{−60x^8y^6}\)
- Answer
-
\(\dfrac{−3y^3}{4x^3}\)
5. \(\dfrac{(10m^5n^4)(5m^3n^6)}{25m^7n^5}\)
6. \(\dfrac{(−18p^4q^7)(−6p^3q^8)}{−36p^{12}q^{10}}\)
- Answer
-
\(\dfrac{−3q^5}{p^5}\)
7. \(\dfrac{(6a^4b^3)(4ab^5)}{(12a^2b)(a^3b)}\)
8. \(\dfrac{(4u^2v^5)(15u^3v)}{(12u^3v)(u^4v)}\)
- Answer
-
\(\dfrac{5v^4}{u^2}\)
Divide a Polynomial by a Monomial
In the following exercises, divide each polynomial by the monomial.
9. \((9n^4+6n^3)÷3n\)
10. \((8x^3+6x^2)÷2x\)
- Answer
-
\(4x^2+3x\)
11. \((63m^4−42m^3)÷(−7m^2)\)
12. \((48y^4−24y^3)÷(−8y^2)\)
- Answer
-
\(−6y^2+3y\)
13. \(\dfrac{66x^3y^2−110x^2y^3−44x^4y^3}{11x^2y^2}\)
14. \(\dfrac{72r^5s^2+132r^4s^3−96r^3s^5}{12r^2s^2}\)
- Answer
-
\(6r^3+11r^2s−8rs^3\)
15. \(10x^2+5x−4−5x\)
16. \(20y^2+12y−1−4y\)
- Answer
-
\(−5y−3+\dfrac{1}{4y}\)
Divide Polynomials using Long Division
In the following exercises, divide each polynomial by the binomial.
17. \((y^2+7y+12)÷(y+3)\)
18. \((a^2−2a−35)÷(a+5)\)
- Answer
-
\(a−7\)
19. \((6m^2−19m−20)÷(m−4)\)
20. \((4x^2−17x−15)÷(x−5)\)
- Answer
-
\(4x+3\)
21. \((q^2+2q+20)÷(q+6)\)
22. \((p^2+11p+16)÷(p+8)\)
- Answer
-
\(p+3−\dfrac{8}{p+8}\)
23. \((3b^3+b^2+4)÷(b+1)\)
24. \((2n^3−10n+28)÷(n+3)\)
- Answer
-
\(\dfrac{2n^2−6n+8+4}{n+3}\)
25. \((z^3+1)÷(z+1)\)
26. \((m^3+1000)÷(m+10)\)
- Answer
-
\(m^2−10m+100\)
27. \((64x^3−27)÷(4x−3)\)
28. \((125y^3−64)÷(5y−4)\)
- Answer
-
\(25y^2+20x+16\)
Divide Polynomials using Synthetic Division
In the following exercises, use synthetic Division to find the quotient and remainder.
29. \(x^3−6x^2+5x+14\) is divided by \(x+1\)
30. \(x^3−3x^2−4x+12\) is divided by \(x+2\)
- Answer
-
\(x^2−5x+6; \space 0\)
31. \(2x^3−11x^2+11x+12\) is divided by \(x−3\)
32. \(2x^3−11x^2+16x−12\) is divided by \(x−4\)
- Answer
-
\(2x^2−3x+4; \space 4\)
33. \(x^4-5x^2+2+13x+3\) is divided by \(x+3\)
34. \(x^4+x^2+6x−10\) is divided by \(x+2\)
- Answer
-
\(x^3−2x^2+5x−4; \space −2\)
35. \(2x^4−9x^3+5x^2−3x−6\) is divided by \(x−4\)
36. \(3x^4−11x^3+2x^2+10x+6\) is divided by \(x−3\)
- Answer
-
\(3x^3−2x^2−4x−2;\space 0\)
Divide Polynomial Functions
In the following exercises, divide.
37. For functions \(f(x)=x^2−13x+36\) and \(g(x)=x−4\), find ⓐ \(\left(\dfrac{f}{g}\right)(x)\) ⓑ \(\left(\dfrac{f}{g}\right)(−1)\)
38. For functions \(f(x)=x^2−15x+54\) and \(g(x)=x−9\), find ⓐ \(\left(\dfrac{f}{g}\right)(x)\) ⓑ \(\left(\dfrac{f}{g}\right)(−5)\)
- Answer
-
ⓐ \(\left(\dfrac{f}{g}\right)(x)=x−6\)
ⓑ \(\left(\dfrac{f}{g}\right)(−5)=−11\)
39. For functions \(f(x)=x^3+x^2−7x+2\) and \(g(x)=x−2\), find ⓐ \(\left(\dfrac{f}{g}\right)(x)\) ⓑ \(\left(\dfrac{f}{g}\right)(2)\)
40. For functions \(f(x)=x^3+2x^2−19x+12\) and \(g(x)=x−3\), find ⓐ \(\left(\dfrac{f}{g}\right)(x)\) ⓑ \(\left(\dfrac{f}{g}\right)(0)\)
- Answer
-
ⓐ \(\left(\dfrac{f}{g}\right)(x)=x^2+5x−4\)
ⓑ \(\left(\dfrac{f}{g}\right)(0)=−4\)
41. For functions \(f(x)=x^2−5x+2\) and \(g(x)=x^2−3x−1\), find ⓐ \((f·g)(x)\) ⓑ \((f·g)(−1)\)
42. For functions \(f(x)=x^2+4x−3\) and \(g(x)=x^2+2x+4\), find ⓐ \((f·g)(x)\) ⓑ \((f·g)(1)\)
- Answer
-
ⓐ \((f·g)(x)=x^4+6x^3+9x^2+10x−12\); ⓑ \((f·g)(1)=14\)
Use the Remainder and Factor Theorem
In the following exercises, use the Remainder Theorem to find the remainder.
43. \(f(x)=x^3−8x+7\) is divided by \(x+3\)
44. \(f(x)=x^3−4x−9\) is divided by \(x+2\)
- Answer
-
\(−9\)
45. \(f(x)=2x^3−6x−24\) divided by \(x−3\)
46. \(f(x)=7x^2−5x−8\) divided by \(x−1\)
- Answer
-
\(−6\)
In the following exercises, use the Factor Theorem to determine if x−cx−c is a factor of the polynomial function.
47. Determine whether \(x+3\) a factor of \(x^3+8x^2+21x+18\)
48. Determine whether \(x+4\) a factor of \(x^3+x^2−14x+8\)
- Answer
-
no
49. Determine whether \(x−2\) a factor of \(x^3−7x^2+7x−6\)
50. Determine whether \(x−3\) a factor of \(x^3−7x^2+11x+3\)
- Answer
-
yes
Writing Exercises
51. James divides \(48y+6\) by \(6\) this way: \(\dfrac{48y+6}{6}=48y\). What is wrong with his reasoning?
52. Divide \(\dfrac{10x^2+x−12}{2x}\) and explain with words how you get each term of the quotient.
- Answer
-
Answer will vary
53. Explain when you can use synthetic division.
54. In your own words, write the steps for synthetic division for \(x^2+5x+6\) divided by \(x−2\).
- Answer
-
Answers will vary.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section
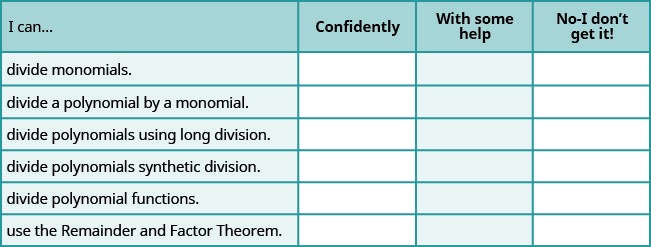
b. On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?


