10.3E: Exercises
- Page ID
- 30569
Practice Makes Perfect
In the following exercises, graph each exponential function.
- \(f(x)=2^{x}\)
- \(g(x)=3^{x}\)
- \(f(x)=6^{x}\)
- \(g(x)=7^{x}\)
- \(f(x)=(1.5)^{x}\)
- \(g(x)=(2.5)^{x}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}\)
- \(g(x)=\left(\frac{1}{3}\right)^{x}\)
- \(f(x)=\left(\frac{1}{6}\right)^{x}\)
- \(g(x)=\left(\frac{1}{7}\right)^{x}\)
- \(f(x)=(0.4)^{x}\)
- \(g(x)=(0.6)^{x}\)
- Answer
-
1.
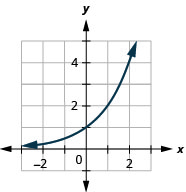
Figure 10.2.22 3.
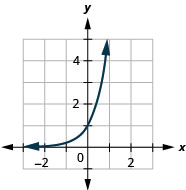
Figure 10.2.23 5.
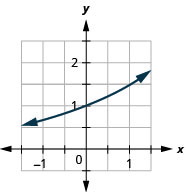
Figure 10.2.24 7.
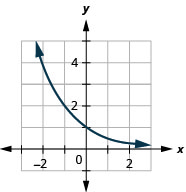
Figure 10.2.25 9.
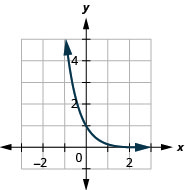
Figure 10.2.26 11.
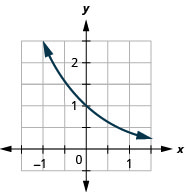
Figure 10.2.27
In the following exercises, graph each function in the same coordinate system.
- \(f(x)=4^{x}, g(x)=4^{x-1}\)
- \(f(x)=3^{x}, g(x)=3^{x-1}\)
- \(f(x)=2^{x}, g(x)=2^{x-2}\)
- \(f(x)=2^{x}, g(x)=2^{x+2}\)
- \(f(x)=3^{x}, g(x)=3^{x}+2\)
- \(f(x)=4^{x}, g(x)=4^{x}+2\)
- \(f(x)=2^{x}, g(x)=2^{x}+1\)
- \(f(x)=2^{x}, g(x)=2^{x}-1\)
- Answer
-
1.
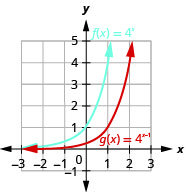
Figure 10.2.28 3.
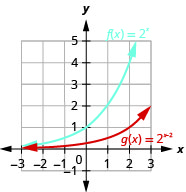
Figure 10.2.29 5.
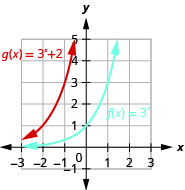
Figure 10.2.30 7.
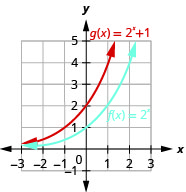
Figure 10.2.31
In the following exercises, graph each exponential function.
- \(f(x)=3^{x+2}\)
- \(f(x)=3^{x-2}\)
- \(f(x)=2^{x}+3\)
- \(f(x)=2^{x}-3\)
- \(f(x)=\left(\frac{1}{2}\right)^{x-4}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}-3\)
- \(f(x)=e^{x}+1\)
- \(f(x)=e^{x-2}\)
- \(f(x)=-2^{x}\)
- \(f(x)=2^{-x-1}-1\)
- Answer
-
1.
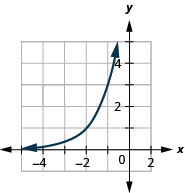
Figure 10.2.32 3.
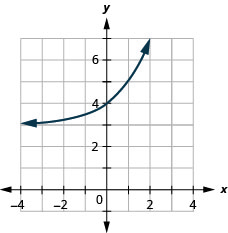
Figure 10.2.33 5.
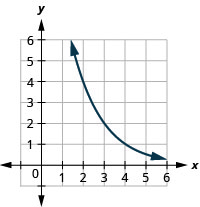
Figure 10.2.34 7.
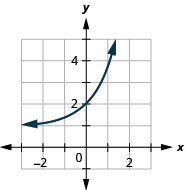
Figure 10.2.35 9.
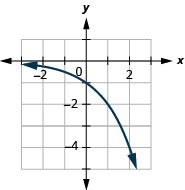
Figure 10.2.36
In the following exercises, solve each equation.
- \(2^{3 x-8}=16\)
- \(2^{2 x-3}=32\)
- \(3^{x+3}=9\)
- \(3^{x^{2}}=81\)
- \(4^{x^{2}}=4\)
- \(4^{x}=32\)
- \(4^{x+2}=64\)
- \(4^{x+3}=16\)
- \(2^{x^{2}+2 x}=\frac{1}{2}\)
- \(3^{x^{2}-2 x}=\frac{1}{3}\)
- \(e^{3 x} \cdot e^{4}=e^{10}\)
- \(e^{2 x} \cdot e^{3}=e^{9}\)
- \(\frac{e^{x^{2}}}{e^{2}}=e^{x}\)
- \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\)
- Answer
-
1. \(x=4\)
3. \(x=-1\)
5. \(x=-1, x=1\)
7. \(x=1\)
9. \(x=-1\)
11. \(x=2\)
13. \(x=-1, x=2\)
In the following exercises, match the graphs to one of the following functions:
- \(2^{x}\)
- \(2^{x+1}\)
- \(2^{x-1}\)
- \(2^{x}+2\)
- \(2^{x}-2\)
- \(3^{x}\)
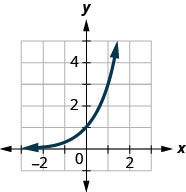
Figure 10.2.37
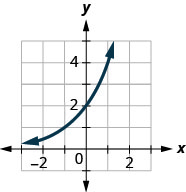
Figure 10.2.38
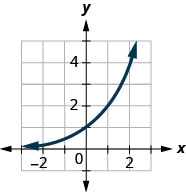
Figure 10.2.39
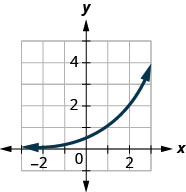
Figure 10.2.40
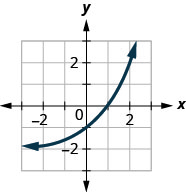
Figure 10.2.41
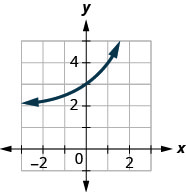
Figure 10.2.42
- Answer
-
1. f
3. a
5. e
In the following exercises, use an exponential model to solve.
- Edgar accumulated $\(5,000\) in credit card debt. If the interest rate is \(20\)% per year, and he does not make any payments for \(2\) years, how much will he owe on this debt in \(2\) years by each method of compounding?
- compound quarterly
- compound monthly
- compound continuously
- Cynthia invested $\(12,000\) in a savings account. If the interest rate is \(6\)%, how much will be in the account in \(10\) years by each method of compounding?
- compound quarterly
- compound monthly
- compound continuously
- Rochelle deposits $\(5,000\) in an IRA. What will be the value of her investment in \(25\) years if the investment is earning \(8\)% per year and is compounded continuously?
- Nazerhy deposits $\(8,000\) in a certificate of deposit. The annual interest rate is \(6\)% and the interest will be compounded quarterly. How much will the certificate be worth in \(10\) years?
- A researcher at the Center for Disease Control and Prevention is studying the growth of a bacteria. He starts his experiment with \(100\) of the bacteria that grows at a rate of \(6\)% per hour. He will check on the bacteria every \(8\) hours. How many bacteria will he find in \(8\) hours?
- A biologist is observing the growth pattern of a virus. She starts with \(50\) of the virus that grows at a rate of \(20\)% per hour. She will check on the virus in \(24\) hours. How many viruses will she find?
- In the last ten years the population of Indonesia has grown at a rate of \(1.12\)% per year to \(258,316,051\). If this rate continues, what will be the population in \(10\) more years?
- In the last ten years the population of Brazil has grown at a rate of \(0.9\)% per year to \(205,823,665\). If this rate continues, what will be the population in \(10\) more years?
- Answer
-
1.
- $\(7,387.28\)
- $\(7,434.57\)
- $\(7,459.12\)
3. $\(36,945.28\)
5. \(223\) bacteria
7. \(288,929,825\)
- Explain how you can distinguish between exponential functions and polynomial functions.
- Compare and contrast the graphs of \(y=x^{2}\) and \(y=2^{x}\).
- What happens to an exponential function as the values of \(x\) decreases? Will the graph ever cross the \(x\)-axis? Explain.
- Answer
-
1. Answers will vary
3. Answers will vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After reviewing this checklist, what will you do to become confident for all objectives?


