11.6E: Exercises
- Page ID
- 30576
Practice Makes Perfect
In the following exercises, solve the system of equations by using graphing.
- \(\left\{\begin{array}{l}{y=2 x+2} \\ {y=-x^{2}+2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=6 x-4} \\ {y=2 x^{2}}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x+y=2} \\ {x=y^{2}}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x-y=-2} \\ {x=y^{2}}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=\frac{3}{2} x+3} \\ {y=-x^{2}+2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=x-1} \\ {y=x^{2}+1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x=-2} \\ {x^{2}+y^{2}=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=-4} \\ {x^{2}+y^{2}=16}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x=2} \\ {(x+2)^{2}+(y+3)^{2}=16}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y-4)^{2}=25}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=-2 x+4} \\ {y=\sqrt{x}+1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=-\frac{1}{2} x+2} \\ {y=\sqrt{x}-2}\end{array}\right.\)
- Answer
-
2.
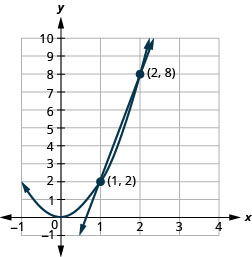
Figure 11.5.61 4.
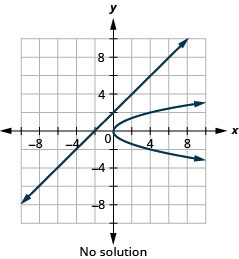
Figure 11.5.62 6.
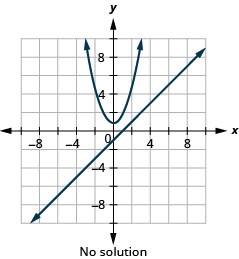
Figure 11.5.63 8.
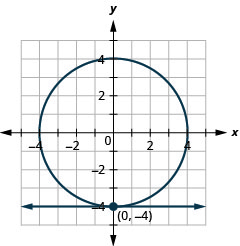
Figure 11.5.64 10.
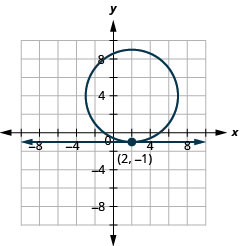
Figure 11.5.65 12.
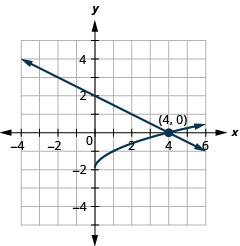
Figure 11.5.66
In the following exercises, solve the system of equations by using substitution.
- \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {y=\frac{1}{2} x-1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x+3}\end{array}\right.\)
- \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=x+3}\end{array}\right.\)
- \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {x=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
- \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{2 y^{2}-x=0} \\ {y=x+1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=x+3}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-y=1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x+y=10}\end{array}\right.\)
- Answer
-
2. \((-1,0),(0,3)\)
4. \((2,0)\)
6. \((12,-5),(12,5)\)
8. No solution
10. \((0,-4),(1,-3)\)
12. \((3,4),(5,0)\)
In the following exercises, solve the system of equations by using elimination.
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y=8}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}+2 y=1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=3}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y^{2}-x=2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x^{2}-3 y^{2}=5}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=20} \\ {x^{2}-y^{2}=-12}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=13} \\ {x^{2}-y^{2}=5}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
- \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}-y^{2}=3} \\ {2 x^{2}+y^{2}=6}\end{array}\right.\)
- \(\left\{\begin{array}{l}{4 x^{2}-y^{2}=4} \\ {4 x^{2}+y^{2}=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}-y^{2}=-5} \\ {3 x^{2}+2 y^{2}=30}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}-y^{2}=1} \\ {x^{2}-2 y=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{2 x^{2}+y^{2}=11} \\ {x^{2}+3 y^{2}=28}\end{array}\right.\)
- Answer
-
2. \((0,-4),(-\sqrt{7}, 3),(\sqrt{7}, 3)\)
4. \((0,-2),(-\sqrt{3}, 1),(\sqrt{3}, 1)\)
6. \((-2,0),(1,-\sqrt{3}),(1, \sqrt{3})\)
8. \((-2,-4),(-2,4),(2,-4),(2,4)\)
10. \((-4,0),(4,0)\)
12. \((-\sqrt{3}, 0),(\sqrt{3}, 0)\)
14. \((-2,-3),(-2,3),(2,-3),(2,3)\)
16. \((-1,-3),(-1,3),(1,-3),(1,3)\)
In the following exercises, solve the problem using a system of equations.
- The sum of two numbers is \(−6\) and the product is \(8\). Find the numbers.
- The sum of two numbers is \(11\) and the product is \(−42\). Find the numbers.
- The sum of the squares of two numbers is \(65\). The difference of the number is \(3\). Find the numbers.
- The sum of the squares of two numbers is \(113\). The difference of the number is \(1\). Find the numbers.
- The difference of the squares of two numbers is \(15\). The difference of twice the square of the first number and the square of the second number is \(30\). Find the numbers.
- The difference of the squares of two numbers is \(20\). The difference of the square of the first number and twice the square of the second number is \(4\). Find the numbers.
- The perimeter of a rectangle is \(32\) inches and its area is \(63\) square inches. Find the length and width of the rectangle.
- The perimeter of a rectangle is \(52\) cm and its area is \(165\) \(\mathrm{cm}^{2}\). Find the length and width of the rectangle.
- Dion purchased a new microwave. The diagonal of the door measures \(17\) inches. The door also has an area of \(120\) square inches. What are the length and width of the microwave door?
- Jules purchased a microwave for his kitchen. The diagonal of the front of the microwave measures \(26\) inches. The front also has an area of \(240\) square inches. What are the length and width of the microwave?
- Roman found a widescreen TV on sale, but isn’t sure if it will fit his entertainment center. The TV is \(60\)”. The size of a TV is measured on the diagonal of the screen and a widescreen has a length that is larger than the width. The screen also has an area of \(1728\) square inches. His entertainment center has an insert for the TV with a length of \(50\) inches and width of \(40\) inches. What are the length and width of the TV screen and will it fit Roman’s entertainment center?
- Donnette found a widescreen TV at a garage sale, but isn’t sure if it will fit her entertainment center. The TV is \(50\)”. The size of a TV is measured on the diagonal of the screen and a widescreen has a length that is larger than the width. The screen also has an area of \(1200\) square inches. Her entertainment center has an insert for the TV with a length of \(38\) inches and width of \(27\) inches. What are the length and width of the TV screen and will it fit Donnette’s entertainment center?
- Answer
-
2. \(-3\) and \(14\)
4. \(-7\) and \(-8\) or \(8\) and \(7\)
6. \(-6\) and \(-4\) or \(-6\) and \(4\) or \(6\) and \(-4\) or \(6\) and \(4\)
8. If the length is \(11\) cm, the width is \(15\) cm. If the length is \(15\) cm, the width is \(11\) cm.
10. If the length is \(10\) inches, the width is \(24\) inches. If the length is \(24\) inches, the width is \(10\) inches.
12. The length is \(40\) inches and the width is \(30\) inches. The TV will not fit Donnette’s entertainment center.
- In your own words, explain the advantages and disadvantages of solving a system of equations by graphing.
- Explain in your own words how to solve a system of equations using substitution.
- Explain in your own words how to solve a system of equations using elimination.
- A circle and a parabola can intersect in ways that would result in \(0, 1, 2, 3,\) or \(4\) solutions. Draw a sketch of each of the possibilities.
- Answer
-
2. Answers may vary
4. Answers may vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?


