12.5: Binomial Theorem
- Page ID
- 5198
By the end of this section, you will be able to:
- Use Pascal’s Triangle to expand a binomial
- Evaluate a binomial coefficient
- Use the Binomial Theorem to expand a binomial
Before you get started, take this readiness quiz.
- Simplify: \(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
If you missed this problem, review Example 1.25. - Expand: \((3 x+5)^{2}\).
If you missed this problem, review Example 5.32. - Expand: \((x-y)^{2}\).
If you missed this problem, review Example 5.32.
Use Pascal's Triangle to Expand a Binomial
In our previous work, we have squared binomials either by using FOIL or by using the Binomial Squares Pattern. We can also say that we expanded \((a+b)^{2}\).
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)
To expand \((a+b)^{3}\), we recognize that this is \((a+b)^{2}(a+b)\) and multiply.
\((a+b)^{3}\)
\((a+b)^{2}(a+b)\)
\(\left(a^{2}+2 a b+b^{2}\right)(a+b)\)
\(a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}\)
\(a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
To find a method that is less tedious that will work for higher expansions like \((a+b)^{7}\), we again look for patterns in some expansions.
| Number of Terms | First Term | Last Term | |
|---|---|---|---|
| \((a+b)^{1}=a+b\) | \(2\) | \(a^{1}\) | \(b^{1}\) |
| \((a+b)^{2}=a^{2}+2 a b+b^{2}\) | \(3\) | \(a^{2}\) | \(b^{2}\) |
| \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\) | \(4\) | \(a^{3}\) | \(b^{3}\) |
| \((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\) | \(5\) | \(a^{4}\) | \(b^{4}\) |
| \((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\) | \(6\) | \(a^{5}\) | \(b^{5}\) |
| \((a+b)^{n}\) | \(n\) | \(a^{n}\) | \(b^{n}\) |
Notice the first and last terms show only one variable. Recall that \(a^{0}=1\), so we could rewrite the first and last terms to include both variables. For example, we could expand \((a+b)^{3}\) to show each term with both variables.
Generally, we don’t show the zero exponents, just as we usually write \(x\) rather than \(1x\).
Patterns in the Expansion of \((a+b)^{n}\)
- The number of terms is \(n+1\).
- The first term is \(a^{n}\) and the last term is \(b^{n}\).
- The exponents on \(a\) decrease by one on each term going left to right.
- The exponents on \(b\) increase by one on each term going left to right.
- The sum of the exponents on any term is \(n\).
Let’s look at an example to highlight the last three patterns.
From the patterns we identified, we see the variables in the expansion of \((a+b)^{n}\), would be
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}\).
To find the coefficients of the terms, we write our expansions again focusing on the coefficients. We rewrite the coefficients to the right forming an array of coefficients.
The array to the right is called Pascal’s Triangle. Notice each number in the array is the sum of the two closest numbers in the row above. We can find the next row by starting and ending with one and then adding two adjacent numbers.
This triangle gives the coefficients of the terms when we expand binomials.
Pascal's Triangle
In the next example, we will use this triangle and the patterns we recognized to expand the binomial.
Use Pascal's Triangle to expand \((x+y)^{6}\).
Solution:
We know the variables for this expansion will follow the pattern we identified. The nonzero exponents of \(x\) will start at six and decrease to one. The nonzero exponents of \(y\) will start at one and increase to six. The sum of the exponents in each term will be six. In our pattern, \(a=x\) and \(b=y\).
\(\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}\)
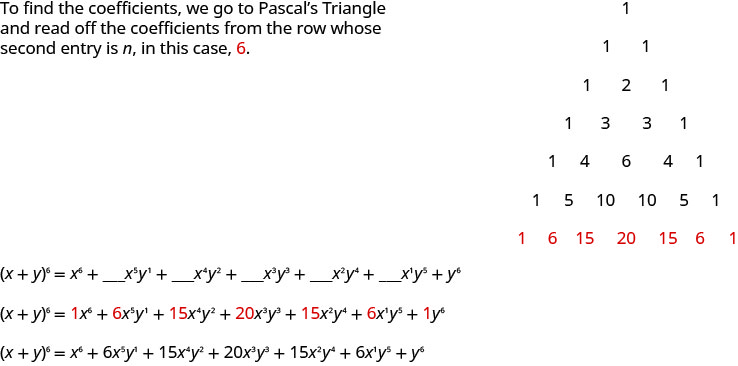
Use Pascal’s Triangle to expand \((x+y)^{5}\).
- Answer
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Use Pascal’s Triangle to expand \((p+q)^{7}\).
- Answer
-
\(\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}\)
In the next example we want to expand a binomial with one variable and one constant. We need to identify the \(a\) and \(b\) to carefully apply the pattern.
Use Pascal’s Triangle to expand \((x+3)^{5}\).
Solution:
We identify the \(a\) and \(b\) of the pattern.
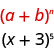
In our pattern, \(a=x\) and \(b=3\).
We know the variables for this expansion will follow the pattern we identified. The sum of the exponents in each term will be five.
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}\)

Use Pascal's Triangle to expand \((x+2)^{4}\).
- Answer
-
\(x^{4}+8 x^{3}+24 x^{2}+32 x+16\)
Use Pascal's Triangle to expand \((x+1)^{6}\).
- Answer
-
\(\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}\)
In the next example, the binomial is a difference and the first term has a constant times the variable. Once we identify the \(a\) and \(b\) of the pattern, we must once again carefully apply the pattern.
Use Pascal's Triangle to expand \((3x-2)^{4}\).
Solution:
We identify the \(a\) and \(b\) of the pattern.
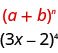
In our pattern, \(a=3x\) and \(b=-2\).

\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.\)
\((3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16\)
\((3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)
Use Pascal's Triangle to expand \((2x-3)^{4}\).
- Answer
-
\(16 x^{4}-96 x^{3}+216 x^{2}-216 x+81\)
Use Pascal's Triangle to expand \((2x-1)^{6}\).
- Answer
-
\(\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}\)
Evaluate a Binomial Coefficient
While Pascal’s Triangle is one method to expand a binomial, we will also look at another method. Before we get to that, we need to introduce some more factorial notation. This notation is not only used to expand binomials, but also in the study and use of probability.
To find the coefficients of the terms of expanded binomials, we will need to be able to evaluate the notation \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) which is called a binomial coefficient. We read \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) as “\(n\) choose \(r\)” or “\(n\) taken \(r\) at a time”.
A binomial coefficient \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\), where \(r\) and \(b\) are integers with \(0 \leq r \leq n\), is defined as
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
We read \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) as "\(n\) choose \(r\)" or "\(n\) taken \(r\) at a time."
Evaluate:
- \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
- \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Solution:
a. We will use the definition of a binomial coefficient,
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
Use the definition, \(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), where \(n=5, r=1\).
\(\frac{5 !}{1 !(5-1) !}\)
Simplify.
\(\frac{5 !}{1 !(4) !}\)
Rewrite \(5!\) as \(5\cdot 4!\)
\(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)
Simplify, by removing common factors.
\(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)
Simplify.
\(5\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)
b. \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
Use the definition, \(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), where \(n=7, r=7\).
\(\frac{7 !}{7 !(7-7) !}\)
Simplify.
\(\frac{7 !}{7 !(0) !}\)
Simplify. Remember \(0!=1\).
\(1\)
\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)
c. \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
Use the definition, \(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), where \(n=4, r=0\).
\(\frac{4 !}{0 !(4-0) !}\)
Simplify.
\(\frac{4 !}{0 !(4) !}\)
Simplify.
\(1\)
\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)
d. \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Use the definition, \(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), where \(n=8, r=5\).
\(\frac{8 !}{5 !(8-5) !}\)
Simplify.
\(\frac{8 !}{5 !(3) !}\)
Rewrite \(8!\) as \(8\cdot 7\cdot 6\cdot 5!\) and remove common factors.
\(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}\)
Simplify.
\(56\)
\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)
Evaluate each binomial coefficient:
- \(\left( \begin{array}{l}{6} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {8}\end{array}\right)\)
- \(\left( \begin{array}{l}{5} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {3}\end{array}\right)\)
- Answer
-
- \(6\)
- \(1\)
- \(1\)
- \(35\)
Evaluate each binomial coefficient:
- \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{11} \\ {11}\end{array}\right)\)
- \(\left( \begin{array}{l}{9} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{6} \\ {5}\end{array}\right)\)
- Answer
-
- \(2\)
- \(1\)
- \(1\)
- \(6\)
In the previous example, \((a)\), \((b)\), \((c)\) demonstrate some special properties of binomial coefficients.
Properties of Binomial Coefficients
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
Use the Binomial Theorem to Expand a Binomial
We are now ready to use the alternate method of expanding binomials. The Binomial Theorem uses the same pattern for the variables, but uses the binomial coefficient for the coefficient of each term.
Binomial Theorem
For any real numbers \(a\) and \(b\), and positive integer \(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Use the Binomial Theorem to expand \((p+q)^{4}\).
Solution:
We identify the \(a\) and \(b\) of the pattern.
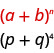
In our pattern, \(a=p\) and \(b=q\).
We use the Binomial Theorem.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substitute in the values \(a=p, b=q\) and \(n=4\).
\((p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Simplify the exponents.
\((p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Evaluate the coefficients, remember, \(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}\)
\((p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}\)
Use the Binomial Theorem to expand \((x+y)^{5}\).
- Answer
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Use the Binomial Theorem to expand \((m+n)^{6}\).
- Answer
-
\(\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}\)
Notice that when we expanded \((p+q)^{4}\) in the last example, using the Binomial Theorem, we got the same coefficients we would get from using Pascal's Triangle.

The next example, the binomial is a difference. When the binomial is a difference, we must be careful in identifying the values we will use in the pattern.
Use the Binomial Theorem to expand \((x-2)^{5}\).
Solution:
We identify the \(a\) and \(b\) of the pattern.
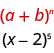
In our pattern, \(a=x\) and \(b=-2\).
We use the Binomial Theorem.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substitute in the values \(a=x, b=-2\), and \(n=5\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
Simplify the coefficients. Remember, \(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
\((x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}\)
\((x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)\)
\((x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32\)
Use the Binomial Theorem to expand \((x-3)^{5}\).
- Answer
-
\(\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}\)
Use the Binomial Theorem to expand \((y-1)^{6}\).
- Answer
-
\(\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}\)
Things can get messy when both terms have a coefficient and a variable.
Use the Binomial Theorem to expand \((2x-3y)^{4}\).
Solution:
We identify the \(a\) and \(b\) of the pattern.
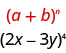
In our pattern, \(a=2x\) and \(b=-3y\).
We use the Binomial Theorem.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substitute in the values \(a=2x, b=-3y\) and \(n=4\).
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}\)
Simplify the exponents.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}\)
Evaluate the coefficients. Remember, \(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}\)
\((2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}\)
\((2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}\)
Use the Binomial Theorem to expand \((3x-2y)^{5}\).
- Answer
-
\(\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}\)
Use the Binomial Theorem to expand \((4x-3y)^{4}\).
- Answer
-
\(\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}\)
The real beauty of the Binomial Theorem is that it gives a formula for any particular term of the expansion without having to compute the whole sum. Let’s look for a pattern in the Binomial Theorem.
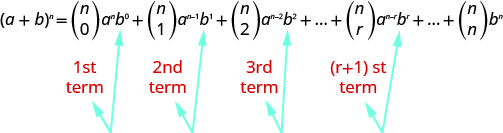
Notice, that in each case the exponent on the \(b\) is one less than the number of the term. The \((r+1)^{st}\) term is the term where the exponent of \(b\) is \(r\). So we can use the format of the \((r+1)^{st}\) term to find the value of a specific term.
Find a Specific Term in a Binomial Expansion
The \((r+1)^{s t}\) term in the expansion of \((a+b)^{n}\) is
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}\)
Find the fourth term of \((x+y)^{7}\).
Solution:
| In our pattern, \(n=7, a=x\) and \(b=y\). | 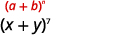 |
|
We are looking for the fourth term. Since \(r+1=4\), then \(r=3\). |
|
| Write the formula | 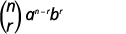 |
| Substitute in the values, \(n=7, r=3, a=x\), and \(b=y\). | 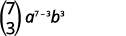 |
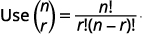 |
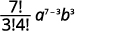 |
| Simplify. | 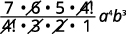 |
| Simplify. |  |
Find the third term of \((x+y)^{6}\).
- Answer
-
\(15x^{4}y^{2}\)
Find the fifth term of \((a+b)^{8}\).
- Answer
-
\(8ab^{7}\)
Find the coefficient of the \(x^{6}\) term of \((x+3)^{9}\).
Solution:
| In our pattern, then \(n=9, a=x\), and \(b=3\). |

|
| We are looking for the coefficient of the \(x^{6}\) term. Since \(a=x\), and \(x^{9-r}=x^{6}\), we know \(r=3\). | |
| Write the formula. |
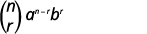
|
| Substitute in the values, \(n=9, 4=3, a=x\), and \(b=3\). |
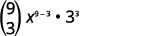
|
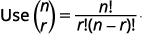
|
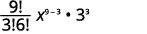
|
| Simplify. |
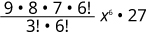
|
| Simplify. |
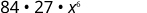
|
| Simplify. |

|
Find the coefficient of the \(x^{5}\) term of \((x+4)^{8}\).
- Answer
-
\(7,168\)
Find the coefficient of the \(x^{4}\) term of \((x+2)^{7}\).
- Answer
-
\(280\)
Access these online resources for additional instruction and practice with sequences.
Key Concepts
- Patterns in the expansion of \((a+b)^{n}\(
- The number of terms is \(n+1\).
- The first term is \(a^{n}\) and the last term is \(b^{n}\).
- The exponents on \(a\) decrease by one on each term going left to right.
- The exponents on \(b\) increase by one on each term going left to right.
- The sum of the exponents on any term is \(n\).
- Pascal’s Triangle

- Binomial Coefficient \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\) : A binomial coefficient \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\), where \(r\) and \(n\) are integers with \(0≤r≤n\), is defined as
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
We read \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) as “\(n\) choose \(r\)” or “\(n\) taken \(r\) at a time”.
- Properties of Binomial Coefficients
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
- Binomial Theorem:
For any real numbers \(a\), \(b\), and positive integer \(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)


