7.3E: Exercises

Last updated
Save as PDF

Page ID: 30324

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Add and Subtract Rational Expressions with a Common Denominator

In the following exercises, add.

1. $\dfrac{2}{15}+\dfrac{7}{15}$

Answer: $\dfrac{3}{5}$

2. $\dfrac{7}{24}+\dfrac{11}{24}$

3. $\dfrac{3c}{4c−5}+\dfrac{5}{4c−5}$

Answer: $\dfrac{3c+5}{4c−5}$

4. $\dfrac{7m}{2m+n}+\dfrac{4}{2m+n}$

5. $\dfrac{2r^2}{2r−1}+\dfrac{15r−8}{2r−1}$

Answer: $r+8$

6. $\dfrac{3s^2}{3s−2}+\dfrac{13s−10}{3s−2}$

7. $\dfrac{2w^2}{w^2−16}+\dfrac{8w}{w^2−16}$

Answer: $\dfrac{2w}{w−4}$

8. $\dfrac{7x^2}{x^2−9}+\dfrac{21x}{x^2−9}$

In the following exercises, subtract.

9. $\dfrac{9a^2}{3a−7}−\dfrac{49}{3a−7}$

Answer: $3a+7$

10. $\dfrac{25b^2}{5b−6}−\dfrac{36}{5b−6}$

11. $\dfrac{3m^2}{6m−30}−\dfrac{21m−30}{6m−30}$

Answer: $\dfrac{m−2}{2}$

12. $\dfrac{2n^2}{4n−32}−\dfrac{18n−16}{4n−32}$

13. $\dfrac{6p^2+3p+4}{p^2+4p−5}−\dfrac{5p^2+p+7}{p^2+4p−5}$

Answer: $\dfrac{p+3}{p+5}$

14. $\dfrac{5q^2+3q−9}{q^2+6q+8}−\dfrac{4q^2+9q+7}{q^2+6q+8}$

15. $\dfrac{5r^2+7r−33}{r^2−49}−\dfrac{4r^2+5r+30}{r^2−49}$

Answer: $\dfrac{r+9}{r+7}$

16. $\dfrac{7t^2−t−4}{t^2−25}−\dfrac{6t^2+12t−44}{t^2−25}$

Add and Subtract Rational Expressions whose Denominators are Opposites

In the following exercises, add or subtract.

17. $\dfrac{10v}{2v−1}+\dfrac{2v+4}{1−2v}$

Answer: $4$

18. $\dfrac{20w}{5w−2}+\dfrac{5w+6}{2−5w}$

19. $\dfrac{10x^2+16x−7}{8x−3}+\dfrac{2x^2+3x−1}{3−8x}$

Answer: $x+2$

20. $\dfrac{6y^2+2y−11}{3y−7}+\dfrac{3y^2−3y+17}{7−3y}$

21. $\dfrac{z^2+6z}{z^2−25}−\dfrac{3z+20}{25−z^2}$

Answer: $\dfrac{z+4}{z−5}$

22. $\dfrac{a^2+3a}{a^2−9}−\dfrac{3a−27}{9−a^2}$

23. $\dfrac{2b^2+30b−13}{b^2−49}−\dfrac{2b^2−5b−8}{49−b^2}$

Answer: $\dfrac{4b−3}{b−7}$

24. $\dfrac{c^2+5c−10}{c^2−16}−\dfrac{c^2−8c−10}{16−c^2}$

Find the Least Common Denominator of Rational Expressions

In the following exercises, a. find the LCD for the given rational expressions b. rewrite them as equivalent rational expressions with the lowest common denominator.

25. $\dfrac{5}{x^2−2x−8},\dfrac{2x}{x^2−x−12}$

Answer: a. $(x+2)(x−4)(x+3)$
b. $\dfrac{5x+15}{(x+2)(x−4)(x+3)}$,
$\dfrac{2x^2+4x}{(x+2)(x−4)(x+3)}$

26. $\dfrac{8}{y^2+12y+35},\dfrac{3y}{y^2+y−42}$

27. $\dfrac{9}{z^2+2z−8},\dfrac{4z}{z^2−4}$

Answer: a. $(z−2)(z+4)(z−4)$
b. $\dfrac{9z−36}{(z−2)(z+4)(z−4)}$,
$\dfrac{4z^2−8z}{(z−2)(z+4)(z−4)}$

28. $\dfrac{6}{a^2+14a+45},\dfrac{5a}{a^2−81}$

29. $\dfrac{4}{b^2+6b+9},\dfrac{2b}{b^2−2b−15}$

Answer: a. $(b+3)(b+3)(b−5)$
b. $\dfrac{4b−20}{(b+3)(b+3)(b−5)}$,
$\dfrac{2b^2+6b}{(b+3)(b+3)(b−5)}$

30. $\dfrac{5}{c^2−4c+4},\dfrac{3c}{c^2−7c+10}$

31. $\dfrac{2}{3d^2+14d−5},\dfrac{5d}{3d^2−19d+6}$

Answer: a. $(d+5)(3d−1)(d−6)$
b. $\dfrac{2d−12}{(d+5)(3d−1)(d−6)}$,
$\dfrac{5d^2+25d}{(d+5)(3d−1)(d−6)}$

32. $\dfrac{3}{5m^2−3m−2},\dfrac{6m}{5m^2+17m+6}$

Add and Subtract Rational Expressions with Unlike Denominators

In the following exercises, perform the indicated operations.

33. $\dfrac{7}{10x^2y}+\dfrac{4}{15xy^2}$

Answer: $\dfrac{21y+8x}{30x^2y^2}$

34. $\dfrac{1}{12a^3b^2}+\dfrac{5}{9a^2b^3}$

35. $\dfrac{3}{r+4}+\dfrac{2}{r−5}$

Answer: $\dfrac{5r−7}{(r+4)(r−5)}$

36. $\dfrac{4}{s−7}+\dfrac{5}{s+3}$

37. $\dfrac{5}{3w−2}+\dfrac{2}{w+1}$

Answer: $\dfrac{11w+1}{(3w−2)(w+1)}$

38. $\dfrac{4}{2x+5}+\dfrac{2}{x−1}$

39. $\dfrac{2y}{y+3}+\dfrac{3}{y−1}$

Answer: $\dfrac{2y^2+y+9}{(y+3)(y−1)}$

40. $\dfrac{3z}{z−2}+\dfrac{1}{z+5}$

41. $\dfrac{5b}{a^2b−2a^2}+\dfrac{2b}{b^2−4}$

Answer: $\dfrac{b(5b+10+2a^2)}{a^2(b−2)(b+2)}$

42. $\dfrac{4}{cd+3c}+\dfrac{1}{d^2−9}$

43. $\dfrac{−3m}{3m−3}+\dfrac{5m}{m^2+3m−4}$

Answer: $-\dfrac{m}{m+4}$

44. $\dfrac{8}{4n+4}+\dfrac{6}{n^2−n−2}$

45. $\dfrac{3r}{r^2+7r+6}+\dfrac{9}{r^2+4r+3}$

Answer: $\dfrac{3(r^2+6r+18)}{(r+1)(r+6)(r+3)}$

46. $\dfrac{2s}{s^2+2s−8}+\dfrac{4}{s^2+3s−10}$

47. $\dfrac{t}{t−6}−\dfrac{t−2}{t+6}$

Answer: $\dfrac{2(7t−6)}{(t−6)(t+6)}$

48. $\dfrac{x−3}{x+6}−\dfrac{x}{x+3}$

49. $\dfrac{5a}{a+3}−\dfrac{a+2}{a+6}$

Answer: $\dfrac{4a^2+25a−6}{(a+3)(a+6)}$

50. $\dfrac{3b}{b−2}−\dfrac{b−6}{b−8}$

51. $\dfrac{6}{m+6}−\dfrac{12m}{m^2−36}$

Answer: $\dfrac{−6}{m−6}$

52. $\dfrac{4}{n+4}−\dfrac{8n}{n^2−16}$

53. $\dfrac{−9p−17}{p^2−4p−21}−\dfrac{p+1}{7−p}$

Answer: $\dfrac{p+2}{p+3}$

54. $\dfrac{−13q−8}{q^2+2q−24}−\dfrac{q+2}{4−q}$

55. $\dfrac{−2r−16}{r^2+6r−16}−\dfrac{5}{2−r}$

Answer: $\dfrac{3}{r−2}$

56. $\dfrac{2t−30}{t^2+6t−27}−\dfrac{2}{3−t}$

57. $\dfrac{2x+7}{10x−1}+3$

Answer: $\dfrac{4(8x+1)}{10x−1}$

58. $\dfrac{8y−4}{5y+2}−6$

59. $\dfrac{3}{x^2−3x−4}−\dfrac{2}{x^2−5x+4}$

Answer: $\dfrac{x−5}{(x−4)(x+1)(x−1)}$

60. $\dfrac{4}{x^2−6x+5}−\dfrac{3}{x^2−7x+10}$

61. $\dfrac{5}{x^2+8x−9}−\dfrac{4}{x^2+10x+9}$

Answer: $\dfrac{1}{(x−1)(x+1)}$

62. $\dfrac{3}{2x^2+5x+2}−\dfrac{1}{2x^2+3x+1}$

63. $\dfrac{5a}{a−2}+\dfrac{9}{a}−\dfrac{2a+18}{a^2−2a}$

Answer: $\dfrac{5a^2+7a−36}{a(a−2)}$

64. $\dfrac{2b}{b−5}+\dfrac{3}{2b}−\dfrac{2b−15}{2b^2−10b}$

65. $\dfrac{c}{c+2}+\dfrac{5}{c−2}−\dfrac{10c}{c^2−4}$

Answer: $\dfrac{c−5}{c+2}$

66. $\dfrac{6d}{d−5}+\dfrac{1}{d+4}+\dfrac{7d−5}{d^2−d−20}$

67. $\dfrac{3d}{d+2}+\dfrac{4}{d}−\dfrac{d+8}{d^2+2d}$

Answer: $\dfrac{3(d+1)}{d+2}$

68. $\dfrac{2q}{q+5}+\dfrac{3}{q−3}−\dfrac{13q+15}{q^2+2q−15}$

Add and Subtract Rational Functions

In the following exercises, find a. $R(x)=f(x)+g(x)$ b. $R(x)=f(x)−g(x)$.

69. $f(x)=\dfrac{−5x−5}{x^2+x−6}$ and $ g(x)=\dfrac{x+1}{2−x}$

Answer: a. $R(x)=−\dfrac{(x+8)(x+1)}{(x−2)(x+3)}$
b. $R(x)=\dfrac{x+1}{x+3}$

70. $f(x)=\dfrac{−4x−24}{x^2+x−30}$ and $ g(x)=\dfrac{x+7}{5−x}$

71. $f(x)=\dfrac{6x}{x^2−64}$ and $g(x)=\dfrac{3}{x−8}$

Answer: a. $R(x)=\dfrac{3(3x+8)}{(x−8)(x+8)}$
b. $R(x)=\dfrac{3}{x+8}$

72. $f(x)=\dfrac{5}{x+7}$ and $ g(x)=\dfrac{10x}{x^2−49}$

Writing Exercises

73. Donald thinks that $\dfrac{3}{x}+\dfrac{4}{x}$ is $\dfrac{7}{2x}$. Is Donald correct? Explain.

Answer: Answers will vary.

74. Explain how you find the Least Common Denominator of $x^2+5x+4$ and $x^2−16$.

75. Felipe thinks $\dfrac{1}{x}+\dfrac{1}{y}$ is $\dfrac{2}{x+y}$.
a. Choose numerical values for x and y and evaluate $\dfrac{1}{x}+\dfrac{1}{y}$.
b. Evaluate $\dfrac{2}{x+y}$ for the same values of x and y you used in part a..
c. Explain why Felipe is wrong.
d. Find the correct expression for $1x+1y$.

Answer: a. Answers will vary.
b. Answers will vary.
c. Answers will vary.
d. $\dfrac{x+y}{x}$

76. Simplify the expression $\dfrac{4}{n^2+6n+9}−\dfrac{1}{n^2−9}$ and explain all your steps.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

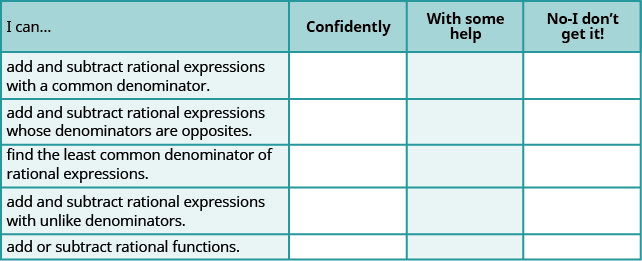
$This table has four columns and six rows. The first row is a header and it labels each column, “I can…”, “Confidently,” “With some help,” and “No-I don’t get it!” In row 2, the I can was add and subtract rational expressions with a common denominator. In row 3, the I can was add and subtract rational expressions with denominators that are opposites. In row 4, the I can find the least common denominator of rational expressions. In row 5, the I can was add and subtract rational expressions with unlike denominators. In row 6, the I can was add or subtract rational functions. There is the nothing in the other columns.$

b. After reviewing this checklist, what will you do to become confident for all objectives?

Search

Text Color

Text Size

Margin Size

Font Type