7.6E: Exercises
- Page ID
- 30803
Solve Proportions
In the following exercises, solve each proportion.
1. \(\dfrac{x}{56}=\dfrac{7}{8}\)
- Answer
-
\(x=49\)
2. \(\dfrac{56}{72}=\dfrac{y}{9}\)
3. \(\dfrac{98}{154}=\dfrac{-7}{p}\)
- Answer
-
\(p=-11\)
4. \(\dfrac{72}{156}=\dfrac{-6}{q}\)
5. \(\dfrac{a}{a+12}=\dfrac{4}{7}\)
- Answer
-
\(a=16\)
6. \(\dfrac{b}{b-16}=\dfrac{11}{9}\)
7. \(\dfrac{m+90}{25}=\dfrac{m+30}{15}\)
- Answer
-
\(m=60\)
8. \(\dfrac{n+10}{4}=\dfrac{40-n}{6}\)
9. \(\dfrac{2 p+4}{8}=\dfrac{p+18}{6}\)
- Answer
-
\(p=30\)
10. \(\dfrac{q-2}{2}=\dfrac{2 q-7}{18}\)
In the following exercises, solve.
- Kevin wants to keep his heart rate at 160 beats per minute while training. During his workout he counts 27 beats in 10 seconds.
- How many beats per minute is this?
- Has Kevin met his target heart rate?
- Answer
-
- 162 beats per minute
- yes
- Jesse’s car gets 30 miles per gallon of gas.
- If Las Vegas is 285 miles away, how many gallons of gas are needed to get there and then home?
- If gas is $3.09 per gallon, what is the total cost of the gas for the trip?
- Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Jocelyn, who weighs 45 pounds?
- Answer
-
9 ml
- A veterinarian prescribed Sunny, a 65-pound dog, an antibacterial medicine in case an infection emerges after her teeth were cleaned. If the dosage is 5 mg for every pound, how much medicine was Sunny given?
- A new energy drink advertises 106 calories for 8 ounces. How many calories are in 12 ounces of the drink?
- Answer
-
159 calories
- One 12-ounce can of soda has 150 calories. If Josiah drinks the big 32-ounce size from the local mini-mart, how many calories does he get?
- Kyra is traveling to Canada and will change $250 US dollars into Canadian dollars. At the current exchange rate, $1 US is equal to $1.3 Canadian. How many Canadian dollars will she get for her trip?
- Answer
-
325 Canadian Dollars
- Maurice is traveling to Mexico and needs to exchange $450 into Mexican pesos. If each dollar is worth 12.29 pesos, how many pesos will he get for his trip?
- Ronald needs a morning breakfast drink that will give him at least 390 calories. Orange juice has 130 calories in one cup. How many cups does he need to drink to reach his calorie goal?
- Answer
-
3 cups
- Sonya drinks a 32-ounce energy drink containing 80 calories per 12 ounce. How many calories did she drink?
- Phil wants to fertilize his lawn. Each bag of fertilizer covers about 4,000 square feet of lawn. Phil’s lawn is approximately 13,500 square feet. How many bags of fertilizer will he have to buy?
- Answer
-
4 bags
- An oatmeal cookie recipe calls for \(\dfrac{1}{2}\) cup of butter to make 4 dozen cookies. Hilda needs to make 10 dozen cookies for the bake sale. How many cups of butter will she need?
Solve Similar Figure Applications
In the following exercises, the triangles are similar. Find the length of the indicated side.
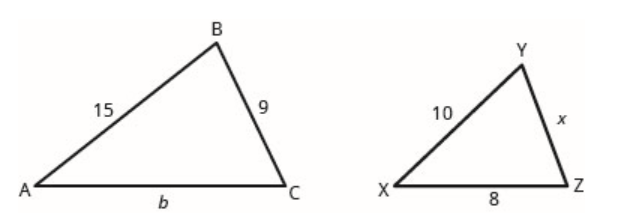
- side x
- side b
- Answer
-
- 6
- 12

- side d
- side q
In the following exercises, use the map shown. On the map, New York City, Chicago, and Memphis form a triangle. The actual distance from New York to Chicago is 800 miles.
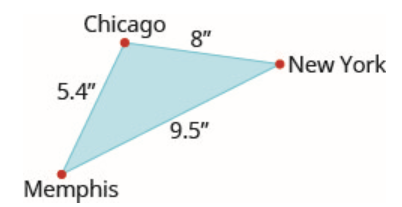
- Find the actual distance from New York to Memphis.
- Answer
-
950 miles
- Find the actual distance from Chicago to Memphis.
In the following exercises, use the map shown. On the map, Atlanta, Miami, and New Orleans form a triangle. The actual distance from Atlanta to New Orleans is 420 miles.
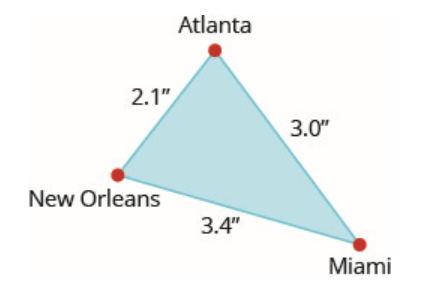
- Find the actual distance from New Orleans to Miami.
- Answer
-
680 miles
- Find the actual distance from Atlanta to Miami.
In the following exercises, answer each question.
- A 2-foot-tall dog casts a 3-foot shadow at the same time a cat casts a one foot shadow. How tall is the cat?
- Answer
-
\(\dfrac{2}{3}\) foot (8 in.)
- Larry and Tom were standing next to each other in the backyard when Tom challenged Larry to guess how tall he was. Larry knew his own height is 6.5 feet and when they measured their shadows, Larry’s shadow was 8 feet and Tom’s was 7.75 feet long. What is Tom’s height?
- The tower portion of a windmill is 212 feet tall. A six foot tall person standing next to the tower casts a seven-foot shadow. How long is the windmill’s shadow?
- Answer
-
247.3 feet
- The height of the Statue of Liberty is 305 feet. Nikia, who is standing next to the statue, casts a 6-foot shadow and she is 5 feet tall. How long should the shadow of the statue be?
Solve Uniform Motion Applications
In the following exercises, solve the application problem provided.
- Mary takes a sightseeing tour on a helicopter that can fly 450 miles against a 35-mph headwind in the same amount of time it can travel 702 miles with a 35-mph tailwind. Find the speed of the helicopter.
- Answer
-
160 mph
- A private jet can fly 1,210 miles against a 25-mph headwind in the same amount of time it can fly 1694 miles with a 25-mph tailwind. Find the speed of the jet.
- A boat travels 140 miles downstream in the same time as it travels 92 miles upstream. The speed of the current is 6mph. What is the speed of the boat?
- Answer
-
29 mph
- Darrin can skateboard 2 miles against a 4-mph wind in the same amount of time he skateboards 6 miles with a 4-mph wind. Find the speed Darrin skateboards with no wind.
- Jane spent 2 hours exploring a mountain with a dirt bike. First, she rode 40 miles uphill. After she reached the peak she rode for 12 miles along the summit. While going uphill, she went 5 mph slower than when she was on the summit. What was her rate along the summit?
- Answer
-
30 mph
- Laney wanted to lose some weight so she planned a day of exercising. She spent a total of 2 hours riding her bike and jogging. She biked for 12 miles and jogged for 6 miles. Her rate for jogging was 10 mph less than biking rate. What was her rate when jogging?
- Byron wanted to try out different water craft. He went 62 miles downstream in a motor boat and 27 miles downstream on a jet ski. His speed on the jet ski was 10 mph faster than in the motor boat. Bill spent a total of 4 hours on the water. What was his rate of speed in the motor boat?
- Answer
-
20 mph
- Nancy took a 3-hour drive. She went 50 miles before she got caught in a storm. Then she drove 68 miles at 9 mph less than she had driven when the weather was good. What was her speed driving in the storm?
- Chester rode his bike uphill 24 miles and then back downhill at 2 mph faster than his uphill. If it took him 2 hours longer to ride uphill than downhill, what was his uphill rate?
- Answer
-
4 mph
- Matthew jogged to his friend’s house 12 miles away and then got a ride back home. It took him 2 hours longer to jog there than ride back. His jogging rate was 25 mph slower than the rate when he was riding. What was his jogging rate?
- Hudson travels 1080 miles in a jet and then 240 miles by car to get to a business meeting. The jet goes 300 mph faster than the rate of the car, and the car ride takes 1 hour longer than the jet. What is the speed of the car?
- Answer
-
60 mph
- Nathan walked on an asphalt pathway for 12 miles. He walked the 12 miles back to his car on a gravel road through the forest. On the asphalt he walked 2 miles per hour faster than on the gravel. The walk on the gravel took one hour longer than the walk on the asphalt. How fast did he walk on the gravel.
- John can fly his airplane 2800 miles with a wind speed of 50 mph in the same time he can travel 2400 miles against the wind. If the speed of the wind is 50 mph, find the speed of his airplane.
- Answer
-
650 mph
- Jim’s speedboat can travel 20 miles upstream against a 3-mph current in the same amount of time it travels 22 miles downstream with a 3-mph current speed . Find the speed of the Jim’s boat.
- Hazel needs to get to her granddaughter’s house by taking an airplane and a rental car. She travels 900 miles by plane and 250 miles by car. The plane travels 250 mph faster than the car. If she drives the rental car for 2 hours more than she rode the plane, find the speed of the car.
- Answer
-
50 mph
- Stu trained for 3 hours yesterday. He ran 14 miles and then biked 40 miles. His biking speed is 6 mph faster than his running speed. What is his running speed?
- When driving the 9-hour trip home, Sharon drove 390 miles on the interstate and 150 miles on country roads. Her speed on the interstate was 15 more than on country roads. What was her speed on country roads?
- Answer
-
50 mph
- Two sisters like to compete on their bike rides. Tamara can go 4 mph faster than her sister, Samantha. If it takes Samantha 1 hours longer than Tamara to go 80 miles, how fast can Samantha ride her bike?
- Dana enjoys taking her dog for a walk, but sometimes her dog gets away, and she has to run after him. Dana walked her dog for 7 miles but then had to run for 1 mile, spending a total time of 2.5 hours with her dog. Her running speed was 3 mph faster than her walking speed. Find her walking speed.
- Answer
-
4.2 mph
- Ken and Joe leave their apartment to go to a football game 45 miles away. Ken drives his car 30 mph faster Joe can ride his bike. If it takes Joe 2 hours longer than Ken to get to the game, what is Joe’s speed?
Solve Work Applications
- Mike, an experienced bricklayer, can build a wall in 3 hours, while his son, who is learning, can do the job in 6 hours. How long does it take for them to build a wall together?
- Answer
-
2 hours
- It takes Sam 4 hours to rake the front lawn while his brother, Dave, can rake the lawn in 2 hours. How long will it take them to rake the lawn working together?
- Mia can clean her apartment in 6 hours while her roommate can clean the apartment in 5 hours. If they work together, how long would it take them to clean the apartment?
- Answer
-
2 hours and 44 minutes
- Brian can lay a slab of concrete in 6 hours, while Greg can do it in 4 hours. If Brian and Greg work together, how long will it take?
- Josephine can correct her students test papers in 5 hours, but if her teacher’s assistant helps, it would take them 3 hours. How long would it take the assistant to do it alone?
- Answer
-
7 hours and 30 minutes
- Washing his dad’s car alone, eight year old Levi takes 2.5 hours. If his dad helps him, then it takes 1 hour. How long does it take Levi’s dad to wash the car by himself?
- At the end of the day Dodie can clean her hair salon in 15 minutes. Ann, who works with her, can clean the salon in 30 minutes. How long would it take them to clean the shop if they work together?
- Answer
-
10 min
- Ronald can shovel the driveway in 4 hours, but if his brother Donald helps it would take 2 hours. How long would it take Donald to shovel the driveway alone?
Solve Direct Variation Problems
In the following exercises, solve.
- If \(y\) varies directly as \(x\) and \(y=14\), when \(x=3\). Find the equation that relates \(x\) and \(y\).
- Answer
-
\(y=\dfrac{14}{3} x\)
- If \(a\) varies directly as \(b\) and \(a=16\), when \(b=4\). Find the equation that relates \(a\) and \(b\).
- If \(p\) varies directly as \(q\) and \(p=9\), when \(q=3\). Find the equation that relates \(p\) and \(q\).
- Answer
-
\(p=3.2 q\)
- If \(v\) varies directly as \(w\) and \(v=8\), when \(w=12\). Find the equation that relates \(v\) and \(w\).
- The price, \(P\), that Eric pays for gas varies directly with the number of gallons, \(g\), he buys. It costs him $50 to buy 20 gallons of gas.
- Write the equation that relates \(P\) and \(g\).
- How much would 33 gallons cost Eric?
- Answer
-
- \(P=2.5 g\)
- \(\$ 82.50\)
- Joseph is traveling on a road trip. The distance, \(d\), he travels before stopping for lunch varies directly with the speed, \(v\), he travels. He can travel 120 miles at a speed of 60 mph.
- Write the equation that relates \(d\) and \(v\).
- How far would he travel before stopping for lunch at a rate of 65 mph?
- The mass of a liquid varies directly with its volume. A liquid with mass 16 kilograms has a volume of 2 liters.
- Write the equation that relates the mass to the volume.
- What is the volume of this liquid if its mass is 128 kilograms?
- Answer
-
- \(m=8 v\)
- 16 liters
- The length that a spring stretches varies directly with a weight placed at the end of the spring. When Sarah placed a 10-pound watermelon on a hanging scale, the spring stretched 5 inches.
- Write the equation that relates the length of the spring to the weight.
- What weight of watermelon would stretch the spring 6 inches?
- The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 6 inch will support a maximum load of 108 pounds.
- Write the equation that relates the load to the diagonal of the cross-section.
- What load will a beam with a 10-inch diagonal support?
- Answer
-
- \(L=3 d^{2}\)
- 300 pounds
- The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 square inches.
- Write the equation that relates the area to the radius.
- What is the area of a personal pizza with a radius 4 inches?
Solve Inverse Variation Problems
In the following exercises, solve.
- If \(y\) varies inversely with \(x\) and \(y=5\), when \(x=4\). Find the equation that relates \(x\) and \(y\).
- Answer
-
\(y=\dfrac{20}{x}\)
- If \(p\) varies inversely with \(q\) and \(p=2\), when \(q=1\). Find the equation that relates \(p\) and \(q\).
- If \(v\) varies inversely with \(w\) and \(v=6\), when \(w=12\). Find the equation that relates \(v\) and \(w\).
- Answer
-
\(v=\dfrac{3}{w}\)
- If \(a\) varies inversely with \(b\) and \(a=12\), when \(b=13\). Find the equation that relates \(a\) and \(b\).
In the following exercises, write an inverse variation equation to solve the following problems.
- The fuel consumption (mpg) of a car varies inversely with its weight. A Toyota Corolla weighs 2800 pounds getting 33 mpg on the highway.
- Write the equation that relates the mpg to the car’s weight.
- What would the fuel consumption be for a Toyota Sequoia that weighs 5500 pounds?
- Answer
-
- \(g=\dfrac{92,400}{w}\)
- 16.8 mpg
- A car’s value varies inversely with its age. Jackie bought a 10-year-old car for $2,400.
- Write the equation that relates the car’s value to its age.
- What will be the value of Jackie’s car when it is 15 years old?
- The time required to empty a tank varies inversely as the rate of pumping. It took Ada 5 hours to pump her flooded basement using a pump that was rated at 200 gpm (gallons per minute).
- Write the equation that relates the number of hours to the pump rate.
- How long would it take Ada to pump her basement if she used a pump rated at 400 gpm?
- Answer
-
- \(t=\dfrac{1000}{r}\)
- 2.5 hours
- On a string instrument, the length of a string varies inversely as the frequency of its vibrations. An 11-inch string on a violin has a frequency of 400 cycles per second.
- Write the equation that relates the string length to its frequency.
- What is the frequency of a 10 inch string?
- Paul, a dentist, determined that the number of cavities that develops in his patient’s mouth each year varies inversely to the number of minutes spent brushing each night. His patient, Lori, had four cavities when brushing her teeth 30 seconds (0.5 minutes) each night.
- Write the equation that relates the number of cavities to the time spent brushing.
- How many cavities would Paul expect Lori to have if she had brushed her teeth for 2 minutes each night?
- Answer
-
- \(c=\dfrac{2}{t}\)
- 1 cavity
- Boyle’s law states that if the temperature of a gas stays constant, then the pressure varies inversely to the volume of the gas. Braydon, a scuba diver, has a tank that holds 6 liters of air under a pressure of 220 psi.
- Write the equation that relates pressure to volume.
- If the pressure increases to 330 psi, how much air can Braydon’s tank hold?
- The cost of a ride service varies directly with the distance traveled. It costs $35 for a ride from the city center to the airport, 14 miles away.
- Write the equation that relates the cost, \(c\), with the number of miles, \(m\).
- What would it cost to travel 22 miles with this service?
- Answer
-
- \(c=2.5 m\)
- \(\$ 55\)
- The number of hours it takes Jack to drive from Boston to Bangor is inversely proportional to his average driving speed. When he drives at an average speed of 40 miles per hour, it takes him 6 hours for the trip.
- Write the equation that relates the number of hours, \(h\), with the speed, \(s\).
- How long would the trip take if his average speed was 75 miles per hour?
Writing Exercises
- Marisol solves the proportion \(\dfrac{144}{a}=\dfrac{9}{4}\) by ‘cross multiplying,’ so her first step looks like \(4 \cdot 144=9 \cdot a\) Explain how this differs from the method of solution shown in Example 7.6.2.
- Answer
-
Answers will vary.
- Paula and Yuki are roommates. It takes Paula 3 hours to clean their apartment. It takes Yuki 4 hours to clean the apartment. The equation \(\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{1}{t}\) can be used to find \(t\), the number of hours it would take both of them, working together, to clean their apartment. Explain how this equation models the situation.
- In your own words, explain the difference between direct variation and inverse variation.
- Answer
-
Answers will vary.
- Make up an example from your life experience of inverse variation.


