12.2: Sequences
- Page ID
- 5195
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Write the first few terms of a sequence
- Find a formula for the general term (nth term) of a sequence
- Use factorial notation
- Find the partial sum
- Use summation notation to write a sum
Before you get started, take this readiness quiz.
- Evaluate \(2n+3\) for the integers \(1, 2, 3\), and \(4\).
If you missed this problem, review Example 1.6. - Evaluate \((−1)^{n}\) for the integers \(1, 2, 3\), and \(4\).
If you missed this problem, review Example 1.19. - If \(f(n)=n^{2}+2\), find \(f(1)+f(2)+f(3)\).
If you missed this problem, review Example 3.49.
Write the First Few Terms of a Sequence
Let’s look at the function \(f(x)=2x\) and evaluate it for just the counting numbers.
| \(f(x)=2x\) | |
| \(x\) | \(2x\) |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(6\) |
| \(4\) | \(8\) |
| \(5\) | \(10\) |
| \(...\) | \(...\) |
If we list the function values in order as \(2, 4, 6, 8\), and \(10\), … we have a sequence. A sequence is a function whose domain is the counting numbers.
A sequence is a function whose domain is the counting numbers.
A sequence can also be seen as an ordered list of numbers and each number in the list is a term. A sequence may have an infinite number of terms or a finite number of terms. Our sequence has three dots (ellipsis) at the end which indicates the list never ends. If the domain is the set of all counting numbers, then the sequence is an infinite sequence. Its domain is all counting numbers and there is an infinite number of counting numbers.
\(2,4,6,8,10, \dots\)
If we limit the domain to a finite number of counting numbers, then the sequence is a finite sequence. If we use only the first four counting numbers, \(1, 2, 3, 4\) our sequence would be the finite sequence,
\(2,4,6,8\)
Often when working with sequences we do not want to write out all the terms. We want more compact way to show how each term is defined. When we worked with functions, we wrote \(f(x)=2x\) and we said the expression \(2x\) was the rule that defined values in the range. While a sequence is a function, we do not use the usual function notation. Instead of writing the function as \(f(x)=2x\), we would write it as \(a_{n}=2n\). The \(a_{n}\) is the \(n\)th term of the sequence, the term in the \(n\)th position where \(n\) is a value in the domain. The formula for writing the \(n\)th term of the sequence is called the general term or formula of the sequence.
The general term of the sequence is found from the formula for writing the \(n\)th term of the sequence. The \(n\)th term of the sequence, \(a_{n}\), is the term in the \(n\)th position where \(n\) is a value in the domain.
When we are given the general term of the sequence, we can find the terms by replacing \(n\) with the counting numbers in order. For \(a_{n}=2 n\),
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(a_{n}\) | 2\(\cdot 1\) | 2\(\cdot 2\) | 2\(\cdot 3\) | 2\(\cdot 4\) | 2\(\cdot 5\) | 2\(\cdot 6\) |
| \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)
\(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)
To find the values of a sequence, we substitute in the counting numbers in order into the general term of the sequence.
Write the first five terms of the sequence whose general term is \(a_{n}=4 n-3\).
Solution:
We substitute the values \(1, 2, 3, 4\), and \(5\) into the formula, \(a_{n}=4n−3\), in order.
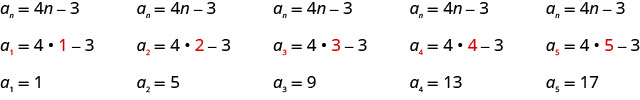
Answer:
The first five terms of the sequence are \(1, 5, 9, 13\), and \(17\).
Write the first five terms of the sequence whose general term is \(a_{n}=3n-4\).
- Answer
-
\(-1,2,5,8,11\)
Write the first five terms of the sequence whose general term is \(a_{n}=2n-5\).
- Answer
-
\(-3,-1,1,3,5\)
For some sequences, the variable is an exponent.
Write the first five terms of the sequence whose general term is \(a_{n}=2^{n}+1\).
Solution:
We substitute the values \(1, 2, 3, 4\), and \(5\) into the formula, \(a_{n}=2^{n}+1\), in order.
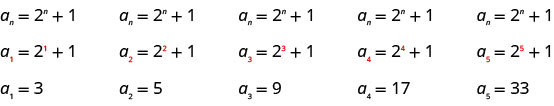
Answer:
The first five terms of the sequence are \(3, 5, 9, 17\), and \(33\).
Write the first five terms of the sequence whose general term is \(a_{n}=3^{n}+4\).
- Answer
-
\(7,13,31,85,247\)
Write the first five terms of the sequence whose general term is \(a_{n}=2^{n}-5\).
- Answer
-
\(-3,-1,3,11,27\)
It is not uncommon to see the expressions \((−1)^{n}\) or \((−1)^{n+1}\) in the general term for a sequence. If we evaluate each of these expressions for a few values, we see that this expression alternates the sign for the terms.
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \((-1)^{n}\) | \((-1)^{1}\) \(-1\) |
\((-1)^{2}\) 1 |
\((-1)^{3}\) \(-1\) |
\((-1)^{4}\) \(1\) |
\((-1)^{5}\) \(-1\) |
| \((-1)^{n+1}\) | \((-1)^{1+1}\) 1 |
\((-1)^{2+1}\) \(-1\) |
\((-1)^{3+1}\) 1 |
\((-1)^{4+1}\) \(-1\) |
\((-1)^{5+1}\) 1 |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)
\(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)
Write the first five terms of the sequence whose general term is \(a_{n}=(-1)^{n} n^{3}\).
Solution:
We substitute the values \(1, 2, 3, 4\), and \(5\) into the formula, \(a_{n}=(-1)^{n} n^{3}\), in order.
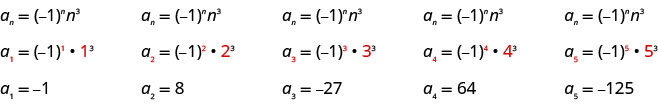
Answer:
The first five terms of the sequence are \(−1, 8, −27, 64, −1, 8, −27, 64\), and \(−125\).
Write the first five terms of the sequence whose general term is \(a_{n}=(-1)^{n} n^{2}\).
- Answer
-
\(-1,4,-9,16,-25\)
Write the first five terms of the sequence whose general term is \(a_{n}=(-1)^{n+1} n^{3}\).
- Answer
-
\(1,-8,27,-64,125\)
Find a Formula for the General Term (\(n\)th Term) of a Sequence
Sometimes we have a few terms of a sequence and it would be helpful to know the general term or \(n\)th term. To find the general term, we look for patterns in the terms. Often the patterns involve multiples or powers. We also look for a pattern in the signs of the terms.
Find a general term for the sequence whose first five terms are shown. \(4,8,12,16,20, \dots\)
Solution:
-
We look for a pattern in the terms. 
The numbers are all multiples of \(4\).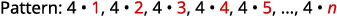 
The general term of the sequence is \(a_{n}=4n\). Table 12.1.4 Answer:
The general term of the sequence is \(a_{n}=4n\).
Find a general term for the sequence whose first five terms are shown.
\(3,6,9,12,15, \dots\)
- Answer
-
\(a_{n}=3 n\)
Find a general term for the sequence whose first five terms are shown.
\(5,10,15,20,25, \dots\)
- Answer
-
\(a_{n}=5 n\)
Find a general term for the sequence whose first five terms are shown. \(2,-4,8,-16,32, \dots\)
Solution:
-
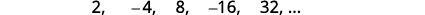
Figure 12.1.8 
Figure 12.1.9 We look for a pattern in the terms.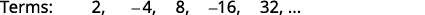 
Figure 12.1.10 The numbers are powers of \(2\). The signs are alternating, with even \(n\) negative.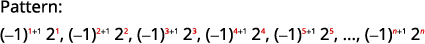 
Figure 12.1.11 The general term of the sequence is \(a_{n}=(-1)^{n+1} 2^{n}\) Table 12.1.5 Answer:
The general term of the sequence is \(a_{n}=(-1)^{n+1}2^{n}\).
Find a general term for the sequence whose first five terms are shown.
\(-3,9,-27,81,-243, \dots\)
- Answer
-
\(a_{n}=(-1)^{n} 3^{n}\)
Find a general term for the sequence whose first five terms are shown
\(1,-4,9,-16,25, \dots\)
- Answer
-
\(a_{n}=(-1)^{n+1} n^{2}\)
Find a general term for the sequence whose first five terms are shown. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)
Solution:
-
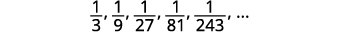
Figure 12.1.12 
Figure 12.1.13 We look for a pattern in the terms.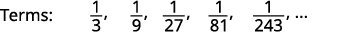 
Figure 12.1.14 The numerators are all \(1\).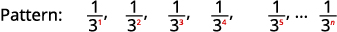 
Figure 12.1.15 The denominators are powers of \(3\). The general term of the sequence is \(a_{n}=\frac{1}{3^{n}}\). Table 12.1.6 Answer:
The general term of the sequence is \(a_{n}=\frac{1}{3^{n}}\).
Find a general term for the sequence whose first five terms are shown.
\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)
- Answer
-
\(a_{n}=\frac{1}{2^{n}}\)
Find a general term for the sequence whose first five terms are shown.
\(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)
- Answer
-
\(a_{n}=\frac{1}{n^{2}}\)
Use Factorial Notation
Sequences often have terms that are products of consecutive integers. We indicate these products with a special notation called factorial notation. For example, \(5!\), read \(5\) factorial, means \(5⋅4⋅3⋅2⋅1\). The exclamation point is not punctuation here; it indicates the factorial notation.
If \(n\) is a positive integer, then \(n!\) is
\(n !=n(n-1)(n-2) \dots\)
We define \(0!\) as \(1\), so \(0!=1\).
The values of \(n!\) for the first \(5\) positive integers are shown.
\(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)
Write the first five terms of the sequence whose general term is \(a_{n}=\frac{1}{n !}\).
Solution:
We substitute the values \(1, 2, 3, 4, 5\) into the formula, \(a_{n}=\frac{1}{n !}\), in order.
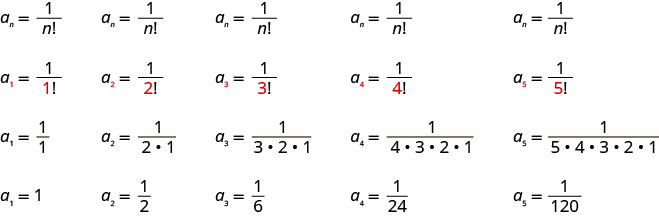
Answer:
The first five terms of the sequence are \(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).
Write the first five terms of the sequence whose general term is \(a_{n}=\frac{2}{n !}\).
- Answer
-
\(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)
Write the first five terms of the sequence whose general term is \(a_{n}=\frac{3}{n !}\).
- Answer
-
\(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)
When there is a fraction with factorials in the numerator and denominator, we line up the factors vertically to make our calculations easier.
Write the first five terms of the sequence whose general term is \(a_{n}=\frac{(n+1) !}{(n-1) !}\).
Solution:
We substitute the values \(1, 2, 3, 4, 5\) into the formula, \(a_{n}=\frac{(n+1) !}{(n-1) !}\), in order.
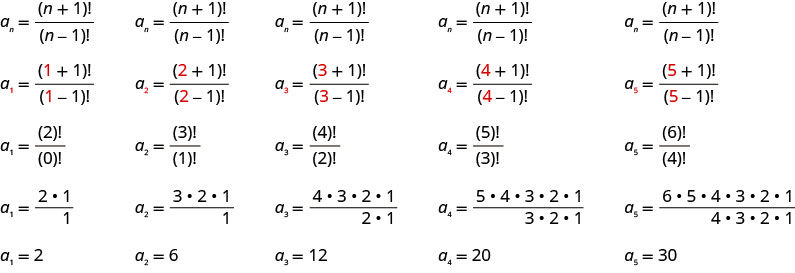
Answer:
The first five terms of the sequence are \(2, 6, 12, 20\), and \(30\).
Write the first five terms of the sequence whose general term is \(a_{n}=\frac{(n-1) !}{(n+1) !}\)
- Answer
-
\(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)
Write the first five terms of the sequence whose general term is \(a_{n}=\frac{n !}{(n+1) !}\).
- Answer
-
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)
Find the Partial Sum
Sometimes in applications, rather than just list the terms, it is important for us to add the terms of a sequence. Rather than just connect the terms with plus signs, we can use summation notation.
For example, \(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) can be written as \(\sum_{i=1}^{5} a_{i}\). We read this as “the sum of \(a\) sub \(i\) from \(i\) equals one to five.” The symbol \(∑\) means to add and the \(i\) is the index of summation. The \(1\) tells us where to start (initial value) and the \(5\) tells us where to end (terminal value).
The sum of the first \(n\) terms of a sequence whose \(n\)th term is \(a_{n}\) is written in summation notation as:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
The \(i\) is the index of summation and the \(1\) tells us where to start and the \(n\) tells us where to end.
When we add a finite number of terms, we call the sum a partial sum.
Expand the partial sum and find its value: \(\sum_{i=1}^{5} 2 i\).
Solution:
-
\(\sum_{i=1}^{5} 2 i\) We substitute the values \(1, 2, 3, 4, 5\) in order. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\) Simplify. \(2+4+6+8+10\) Add. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\) Table 12.1.7 Answer:
\(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
Expand the partial sum and find its value: \(\sum_{i=1}^{5} 3 i\).
- Answer
-
\(45\)
Expand the partial sum and find its value: \(\sum_{i=1}^{5} 4 i\).
- Answer
-
\(60\)
The index does not always have to be \(i\) we can use any letter, but \(i\) and \(k\) are commonly used. The index does not have to start with \(1\) either—it can start and end with any positive integer.
Expand the partial sum and find its value: \(\sum_{k=0}^{3} \frac{1}{k !}\).
Solution:
\(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)
Expand the partial sum and find its value: \(\sum_{k=0}^{3} \frac{2}{k !}\).
- Answer
-
\(\frac{16}{3}\)
Expand the partial sum and find its value: \(\sum_{k=0}^{3} \frac{3}{k !}\).
- Answer
-
\(8\)
Use Summation Notation to Write a Sum
In the last two examples, we went from summation notation to writing out the sum. Now we will start with a sum and change it to summation notation. This is very similar to finding the general term of a sequence. We will need to look at the terms and find a pattern. Often the patterns involve multiples or powers.
Write the sum using summation notation: \(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).
Solution:
\(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)
Write the sum using summation notation: \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).
- Answer
-
\(\sum_{n=1}^{5} \frac{1}{2^{n}}\)
Write the sum using summation notation: \(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)
- Answer
-
\(\sum_{n=1}^{5} \frac{1}{n^{2}}\)
When the terms of a sum have negative coefficients, we must carefully analyze the pattern of the signs.
Write the sum using summation notation: \(-1+8-27+64-125\).
Solution:
-
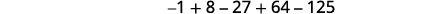
Figure 12.1.18 
Figure 12.1.19 We look for a pattern in the terms. 
Figure 12.1.20 The signs of the terms alternate,
and the odd terms are negative.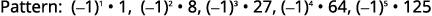
Figure 12.1.21 The numbers are the cubes of the
counting numbers from one to five.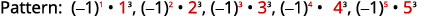
Figure 12.1.22 
Figure 12.1.23 The sum written in summation notation is \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\) Table 12.1.8
Write each sum using summation notation: \(1-4+9-16+25\).
- Answer
-
\(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)
Write each sum using summation notation: \(-2+4-6+8-10\).
- Answer
-
\(\sum_{n=1}^{5}(-1)^{n} 2 n\)
Access this online resource for additional instruction and practice with sequences.
Key Concepts
- Factorial Notation
If \(n\) is a positive integer, then \(n!\) is
\(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)
We define \(0!\) as \(1\), so \(0!=1\)
- Summation Notation
The sum of the first \(n\) terms of a sequence whose \(n\)th term \(a_{n}\) is written in summation notation as:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
The \(i\) is the index of summation and the \(1\) tells us where to start and the \(n\) tells us where to end.
Glossary
- finite sequence
- A sequence with a domain that is limited to a finite number of counting numbers.
- general term of a sequence
- The general term of the sequence is the formula for writing the \(n\)th term of the sequence. The \(n\)th term of the sequence, \(a_{n}\), is the term in the \(n\)th position where \(n\) is a value in the domain.
- infinite sequence
- A sequence whose domain is all counting numbers and there is an infinite number of counting numbers.
- partial sum
- When we add a finite number of terms of a sequence, we call the sum a partial sum.
- sequence
- A sequence is a function whose domain is the counting numbers.