3.2: Compound inequalities
- Page ID
- 45039
Several inequalities are combined together to form compound inequalities. There are three types of compound inequalities which we will investigate in this section: and, or, and tripartite.
Let \(A\) and \(B\) be sets.
- The union of two sets contains all the elements contained in either set (or both sets). The union is denoted \(A ∪ B\).
- The intersection of two sets contains only the elements that are in both sets. The intersection is denoted \(A ∩ B\).
Compound Inequalities with or
For or compound inequalities, the solution is a true statement from either one inequality, the other inequality, or both. This should remind you of the union of two sets except, in this case, we are going to determine the solution by graphing each inequality, and write the solution in interval notation. Hint: We will use the union symbol, \(∪\), in the solution.
Solve the compound inequality. Graph the solution and write the solution in interval notation.
\[2x-5>3\quad\text{or}\quad 4-x\geq 6\nonumber\]
Solution
We begin the solution by solving for each inequality.
\[\begin{array}{rl}2x-5>3\quad\text{or}\quad 4-x\geq 6&\text{Solve each inequality} \\ 2x>8\quad\text{or}\quad -x\geq 2&\text{Divide by the coefficient of }x \\ x>4\quad\text{or}\quad x\leq -2&\text{Solution in inequality notation}\end{array}\nonumber\]
Let’s graph each of these inequalities to determine the union of the two sets.

Looking for the union of these two sets, we see the solution is all the numbers to the left of \(−2\) (inclusive), or to the right of \(4\), or in both. Hence, in interval notation, the solution is \[(-\infty ,-2]\cup (4,\infty )\nonumber\]
The symbol for infinity was first used by the Romans, although, at the time, the number was used for \(1,000\). The Greeks also used the symbol for \(10,000\).
There are special cases with the or compound inequalities when obtaining a solution.
Case 1. As one graph in contained in the other, the union of the two sets will be the larger set.
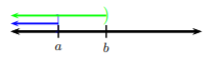
Hence, in this case, the solution is \((-\infty , b)\).

Hence, in this case, the solution is \((−∞, ∞)\).
Compound Inequalities with and
For and compound inequalities, the solution is a true statement from both inequalities. This should remind you of the intersection of two sets except, in this case, we are going to determine the solution by graphing each inequality, and write the solution in interval notation. Hint: The solution is one interval, and no set symbols are used with and problems.
Solve the compound inequality. Graph the solution and write the solution in interval notation.
\[2x+8\geq 5x-7\quad\text{and}\quad 5x-3>3x+1\nonumber\]
Solution
We begin the solution by solving for each inequality.
\[\begin{array}{rl}2x+8\geq 5x-7\quad\text{and}\quad 5x-3>3x+1&\text{Solve each inequality} \\ 8\geq 3x-7\quad\text{and}\quad 2x-3>1 &\text{Isolate the variable term} \\ 15\geq 3x\quad\text{and}\quad 2x>4&\text{Divide by the coefficient of }x \\ 5\geq x\quad\text{and}\quad x>2&\text{Solution in inequality notation}\end{array}\nonumber\]
Let’s graph each of these inequalities to determine the intersection of the two sets.
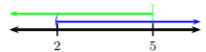
Looking for the intersection of these two sets, we see the solution is all the numbers in between 2 and 5 (inclusive). Hence, in interval notation, the solution is \((2, 5]\).
There are special cases with the and compound inequalities when obtaining a solution.
Case 1. As one graph in contained in the other, the intersection of the two sets will be the smaller set.
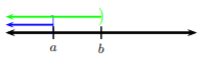
Hence, in this case, the solution is \((−∞, a)\).
Case 2. As the graphs do not intersect, where there is a gap between sets, then there is no solution, i.e., \(∅\).

Hence, in this case, the solution is no solution or \(\emptyset\).
Recall, 3.1.3 from the previous section. Tripartite inequalities are and compound inequalities, where we are find the intersection of the two sets. Notice, the solutions in 3.1.3 were one interval as with and compound inequalities.
Solve the compound inequality. Graph the solution and write the solution in interval notation.
\[-6\leq -4x+2<2\nonumber\]
Solution
We begin the solution by applying the properties of inequalities to every side of the inequality.
\[\begin{array}{rl} -6\leq -4x+2<2&\text{Subtract }2\text{ from all three parts} \\ -8\leq -4x<0&\text{Divide all three parts by }-4 \\ 2\geq x>0&\text{Flip entire statement so values increase from left to right} \\ 0<x\leq 2&\text{Solution in inequality notation}\end{array}\nonumber\]
Let’s graph this inequality to determine the intersection of the two sets.

We can see the intersection is all the numbers in between \(0\) and \(2\) (inclusive). Hence, in interval notation, the solution is \((0, 2]\).
Compound Inequalities Homework
Solve the compound inequalities. Graph the solution and write the solution in interval notation.
\(\frac{n}{3}\leq -3\) or \(-5n\leq -10\)
\(x + 7 ≥ 12\) or \(9x < −45\)
\(x − 6 < −13\) or \(6x ≤ −60\)
\(\frac{v}{8} > −1\) and \(v − 2 < 1\)
\(−8 + b < −3\) and \(4b < 20\)
\(a + 10 ≥ 3\) and \(8a ≤ 48\)
\(3 ≤ 9 + x ≤ 7\)
\(11 < 8 + k ≤ 12\)
\(−3 < x − 1 < 1\)
\(−4 < 8 − 3m ≤ 11\)
\(−16 ≤ 2n − 10 ≤ −22\)
\(−5b + 10 ≤ 30\) and \(7b + 2 ≤ −40\)
\(3x − 9 < 2x + 10\) and \(5 + 7x ≤ 10x − 10\)
\(−8 − 6v ≤ 8 − 8v\) and \(7v + 9 ≤ 6 + 10v\)
\(1 + 5k ≤ 7k − 3\) or \(k − 10 > 2k + 10\)
\(2x + 9 ≥ 10x + 1\) and \(3x − 2 < 7x + 2\)
\(6m ≥ −24\) or \(m − 7 < −12\)
\(10r > 0\) or \(r − 5 < −12\)
\(9 + n < 2\) or \(5n > 40\)
\(−9x < 63\) and \(\frac{x}{4} < 1\)
\(−6n ≤ 12\) and \(\frac{n}{3}≤ 2\)
\(−6 + v ≥ 0\) and \(2v > 4\)
\(0 ≥ \frac{x}{9} ≥ −1\)
\(−11 ≤ n − 9 ≤ −5\)
\(1 ≤ \frac{p}{8} ≤ 0\)
\(3 + 7r > 59\) or \(−6r − 3 > 33\)
\(−6 − 8x ≥ −6\) or \(2 + 10x > 82\)
\(n + 10 ≥ 15\) or \(4n − 5 < −1\)
\(4n + 8 < 3n − 6\) or \(10n − 8 ≥ 9 + 9n\)
\(5 − 2a ≥ 2a + 1\) or \(10a − 10 ≥ 9a + 9\)
\(8 − 10r ≤ 8 + 4r\) or \(−6 + 8r < 2 + 8r\)
\(−9m + 2 < −10 − 6m\) or \(−m + 5 ≥ 10 + 4m\)


