1.7: The Exponential Function
- Page ID
- 47203
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
We have Euler's formula: \(e^{i\theta} = \cos (\theta) + i \sin (\theta)\). We can extend this to the complex exponential function \(e^z\).
For \(z = x + iy\) the complex exponential function is defined as
\[e^z = e^{x + iy} = e^x e^{iy} = e^x (\cos (y) + i \sin (y)). \nonumber \]
In this definition \(e^x\) is the usual exponential function for a real variable \(x\).
It is easy to see that all the usual rules of exponents hold:
- \(e^0 = 1\)
- \(e^{z_1 + z_2} = e^{z_1} e^{z_2}\)
- \((e^z)^n = e^{nz}\) for positive integers \(n\).
- \((e^z)^{-1} = e^{-z}\)
- \(e^z \ne 0\)
It will turn out that the property \(\dfrac{de^z}{dz} = e^z\) also holds, but we can’t prove this yet because we haven’t defined what we mean by the complex derivative \(\dfrac{d}{dz}\).
Here are some more simple, but extremely important properties of \(e^z\). You should become fluent in their use and know how to prove them. - \(|e^{i \theta}| = 1\)
Proof.
\(|e^{i \theta}| = |\cos (\theta) + i \sin (\theta)| = \sqrt{\cos ^2 (\theta) + \sin ^2 (\theta)} = 1\) - \(|e^{x + iy}| = e^x\) (as usual \(z = x + iy\) and \(x, y\) are real).
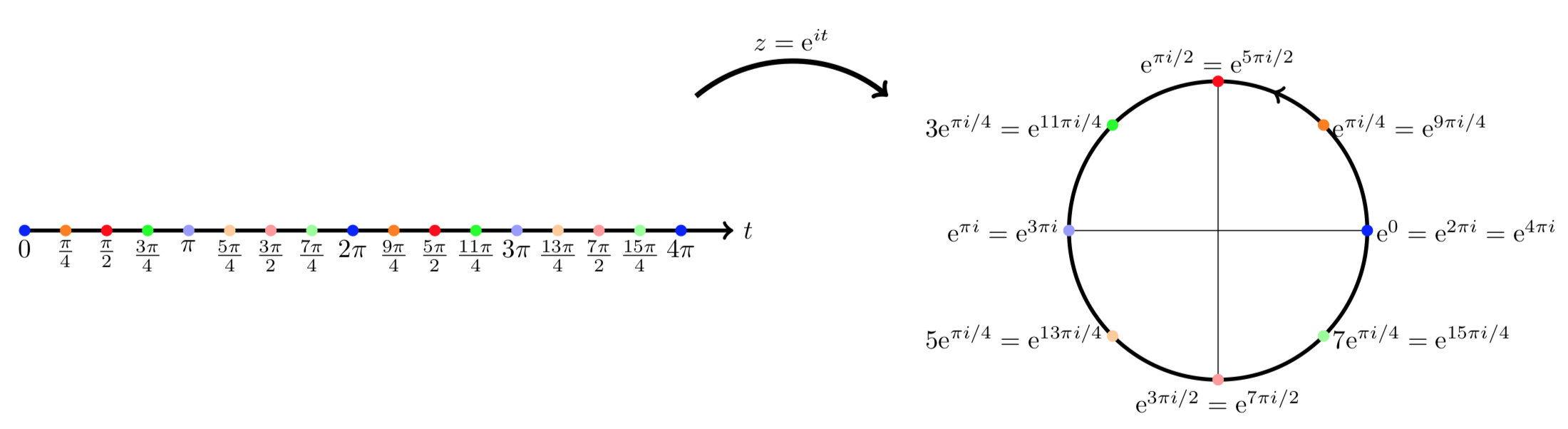
Proof. You should be able to supply this. If not: ask a teacher or TA. - The path \(e^{it}\) for \(0 < t < \infty\) wraps counterclockwise around the unit circle. It does so infinitely many times. This is illustrated in the following picture.