3.8: Open and Closed Sets. Neighborhoods
- Page ID
- 20135
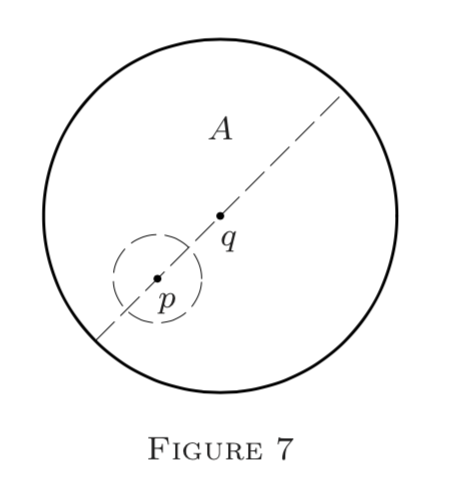
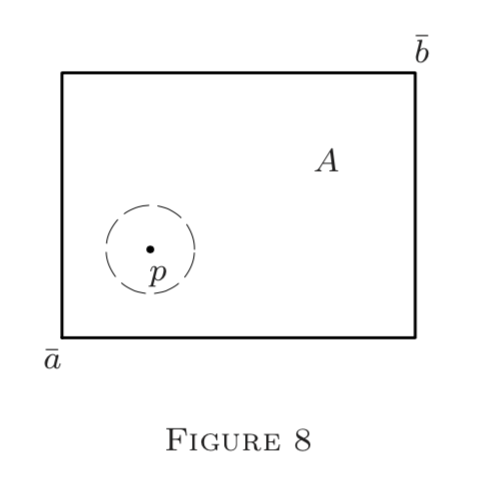
I. Let \(A\) be an open globe in \((S, \rho)\) or an open interval \((\overline{a}, \overline{b})\) in \(E^{n} .\) Then every \(p \in A\) can be enclosed in a small globe \(G_{p}(\delta) \subseteq A(\) Figures 7 and 8\()\). (This would fail for "boundary" points; but there are none inside an open \(G_{q}\) or \((\overline{a}, \overline{b}) . )\).
This suggests the following ideas, for any \((S, \rho)\).
A point \(p\) is said to be interior to a set \(A \subseteq(S, \rho)\) iff \(A\) contains some \(G_{p} ;\) i.e., \(p,\) together with some globe \(G_{p},\) belongs to \(A .\) We then also say that \(A\) is a neighborhood of \(p .\) The set of all interior points of \(A\) ("the interior of \(A^{\prime \prime}\) is denoted \(A^{0} .\) Note: \(\emptyset^{0}=\emptyset\) and \(S^{0}=S !\)
\(\mathrm{A}\) set \(A \subseteq(S, \rho)\) is said to be open iff \(A\) coincides with its interior \(\left(A^{0}=A\right) .\) Such are \(\emptyset\) and \(S .\)
(1) As noted above, an open globe \(G_{q}(r)\) has interior points only, and thus is an open set in the sense of Definition \(2 .\) (See Problem 1 for a proof.)
(2) The same applies to an open interval \((\overline{a}, \overline{b})\) in \(E^{n} .\) (See Problem \(2 . )\)
(3) The interior of any interval in \(E^{n}\) never includes its endpoints \(\overline{a}\) and \(\overline{b}\). In fact, it coincides with the open interval \((\overline{a}, \overline{b}) .\) (See Problem \(4 . )\)
(4) The set \(R\) of all rationals in \(E^{1}\) has no interior points at all \(\left(R^{0}=\emptyset\right)\) because it cannot contain any \(G_{p}=(p-\varepsilon, p+\varepsilon) .\) Indeed, any such \(G_{p}\) contains irrationals (see Chapter 2, §§11-12, Problem 5\(),\) so it is not entirely contained in \(R .\)
(Hausdorff property). Any two points \(p\) and \(q\) \((p \neq q)\) in \((S, \rho)\) are centers of two disjoint globes.
More precisely,
\[(\exists \varepsilon>0) \quad G_{p}(\varepsilon) \cap G_{q}(\varepsilon)=\emptyset.\]
- Proof
-
As \(p \neq q,\) we have \(\rho(p, q)>0\) by metric axiom \(\left(\mathrm{i}^{\prime}\right) .\) Thus we may put
\[\varepsilon=\frac{1}{2} \rho(p, q)>0.\]
It remains to show that with this \(\varepsilon, G_{p}(\varepsilon) \cap G_{q}(\varepsilon)=\emptyset\).
Seeking a contradiction, suppose this fails. Then there is \(x \in G_{p}(\varepsilon) \cap G_{q}(\varepsilon)\) so that \(\rho(p, x)<\varepsilon\) and \(\rho(x, q)<\varepsilon .\) By the triangle law,
\[\rho(p, q) \leq \rho(p, x)+\rho(x, q)<\varepsilon+\varepsilon=2 \varepsilon ; \text{ i.e., } \rho(p, q)<2 \varepsilon,\]
which is impossible since \(\rho(p, q)=2 \varepsilon . \square\)
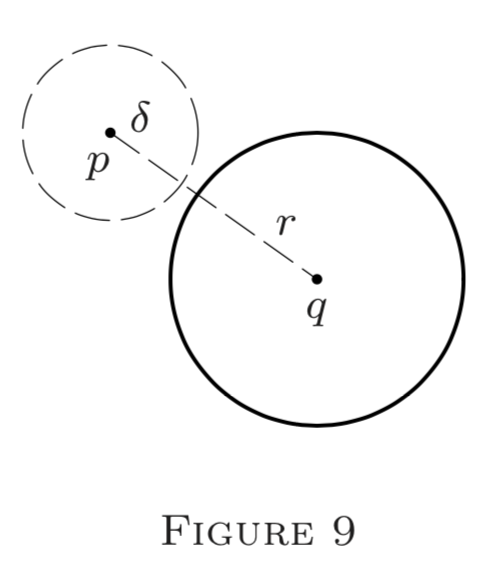
Note. A look at Figure 9 explains the idea of this proof, namely, to obtain two disjoint globes of equal radius, it suffices to choose \(\varepsilon \leq \frac{1}{2} \rho(p, q) .\) The reader is advised to use such diagrams in \(E^{2}\) as a guide.
II. We can now define closed sets in terms of open sets.
A set \(A \subseteq(S, \rho)\) is said to be closed iff its complement \(-A=S-A\) is open, i.e., has interior points only.
That is, each \(p \in-A\) (outside \(A )\) is in some globe \(G_{p} \subseteq-A\) so that
\[A \cap G_{p}=\emptyset.\]
(Continued).
(5) The sets \(\emptyset\) and \(S\) are closed, for their complements, \(S\) and \(\emptyset,\) are open, as noted above. Thus a set may be both closed and open ("clopen").
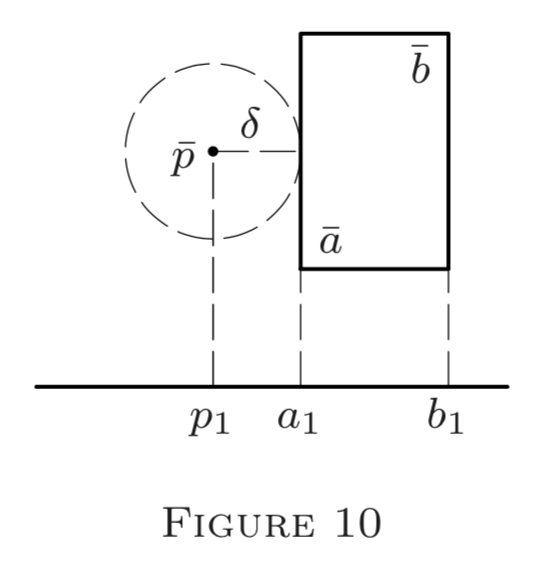
(6) All closed globes in \((S, \rho)\) and all closed intervals in \(E^{n}\) are closed sets by Definition \(3 .\) Indeed (see Figures 9 and \(10 ),\) if \(A=\overline{G}_{q}(r)\) or \(A=[\overline{a}, \overline{b}]\), then any point \(p\) outside \(A\) can be enclosed in a globe \(G_{p}(\delta)\) disjoint from \(A ;\) so, by Definition \(3, A\) is closed (see Problem 12\()\).
(7) A one-point set \(\{q\}\) (also called "singleton") in \((S, \rho)\) is always closed, for any \(p\) outside \(\{q\}(p \neq q)\) is in a globe disjoint from \(\{q\}\) by Theorem 1 In a discrete space (§§11,) Example (3)), \(\{q\}\) is also open since it is an open \(g\) lobe, \(\{q\}=G_{q}\left(\frac{1}{2}\right)(\) why? \() ;\) so it is "clopen. " Hence, in such a space, all sets are "clopen". For \(p \in A\) implies \(\{p\}=G_{p}\left(\frac{1}{2}\right) \subseteq A ;\) similarly for \(-A .\) Thus \(A\) and \(-A\) have interior points only, so both are open.
(8) The interval \((a, b]\) in \(E^{1}\) is neither open nor closed. (Why?)
III. (The rest of this section may be deferred until Chapter (4, §10.)
The union of any finite or infinite family of open sets \(A_{i}(i \in I)\), denoted
\[\bigcup_{i \in I} A_{i},\]
is open itself. So also is
\[\bigcap_{i=1}^{n} A_{i}\]
for finitely many open sets. (This fails for infinitely many sets \(A_{i} ;\) see Problem 11 below.)
- Proof
-
We must show that any point \(p\) of \(A=\bigcup_{i} A_{i}\) is interior to \(A\).
Now if \(p \in \bigcup_{i} A_{i}, p\) is in some \(A_{i},\) and it is an interior point of \(A_{i}\) (for \(A_{i}\) is open, by assumption). Thus there is a globe
\[G_{p} \subseteq A_{i} \subseteq A,\]
as required.
For finite intersections, it suffices to consider two open sets \(A\) and \(B\) (for \(n\) sets, all then follows by induction). We must show that each \(p \in A \cap B\) is interior to \(A \cap B .\)
Now as \(p \in A\) and \(A\) is open, we have some \(G_{p}\left(\delta^{\prime}\right) \subseteq A .\) Similarly, there is \(G_{p}\left(\delta^{\prime \prime}\right) \subseteq B .\) Then the smaller of the two globes, call it \(G_{p},\) is in both \(A\) and \(B,\) so
\[G_{p} \subseteq A \cap B\]
and \(p\) is interior to \(A \cap B,\) indeed. \(\square\)
If the sets \(A_{i}(i \in I)\) are closed, so is
\[\bigcap_{i \in I} A_{i}\]
(even for infinitely many sets). So also is
\[\bigcup_{i=1}^{n} A_{i}\]
for finitely many closed sets \(A_{i} .\) (Again, this fails for infinitely many sets \(A_{i} . )\)
- Proof
-
Let \(A=\bigcap_{i \in I} A_{i} .\) To prove that \(A\) is closed, we show that \(-A\) is open.
Now by set theory (see Chapter 1, §§1-3, Theorem 2) ,
\[-A=-\bigcap_{i} A_{i}=\bigcup_{i}\left(-A_{i}\right),\]
where the \(\left(-A_{i}\right)\) are open (for the \(A_{i}\) are closed \() .\) Thus by Theorem \(2,-A\) is open, as required.
The second assertion (as to \(\bigcup_{i=1}^{n} A_{i} )\) follows quite similarly. \(\square\)
\(A\) nonempty set \(A \subseteq(S, \rho)\) is open iff \(A\) is a union of open globes.
For if \(A\) is such a union, it is open by Theorem \(2 .\) Conversely, if \(A\) is open, then each \(p \in A\) is in some \(G_{p} \subseteq A .\) All such \(G_{p}(p \in A)\) cover all of \(A,\) so \(A \subseteq \bigcup_{p \in A} G_{p} .\) Also, \(\bigcup_{p \in A} G_{p} \subseteq A\) since all \(G_{p}\) are in \(A .\) Thus
\[A=\bigcup_{p \in A} G_{p}.\]
Every finite set \(F\) in a metric space \((S, \rho)\) is closed.
- Proof
-
If \(F=\emptyset, F\) is closed by Example \((5) .\) If \(F \neq \emptyset,\) let
\[F=\left\{p_{1}, \ldots, p_{n}\right\}=\bigcup_{k=1}^{n}\left\{p_{k}\right\}.\]
Now by Example \((7),\) each \(\left\{p_{k}\right\}\) is closed; hence so is \(F\) by by theorem \(3 . \square\)
Note. The family of all open sets in a given space \((S, \rho)\) is denoted by \(\mathcal{G}\); that of all closed sets, by \(\mathcal{F} .\) Thus \(" A \in \mathcal{G}^{\prime \prime}\) means that \(A\) is open; "A \(\in \mathcal{F}^{\prime \prime}\) means that \(A\) is closed. By Theorems 2 and \(3,\) we have
\[(\forall A, B \in \mathcal{G}) \quad A \cup B \in \mathcal{G} \text{ and } A \cap B \in \mathcal{G};\]
similarly for \(\mathcal{F} .\) This is a kind of "closure law." We say that \(\mathcal{F}\) and \(\mathcal{G}\) are "closed under finite unions and intersections."
In conclusion, consider any subspace \((A, \rho)\) of \((S, \rho) .\) As we know from §11 it is a metric space itself, so it has its own open and closed sets (which must consist of points of \(A\) only \() .\) We shall now show that they are obtained from those of \((S, \rho)\) by intersecting the latter sets with \(A .\)
Let \((A, \rho)\) be a subspace of \((S, \rho) .\) Then the open (closed) sets in \((A, \rho)\) are exactly all sets of the form \(A \cap U,\) with \(U\) open \((\)closed\()\) in \(S\).
- Proof
-
Let \(G\) be open in \((A, \rho) .\) By Corollary \(1, G\) is the union of some open globes \(G_{i}^{*}(i \in I)\) in \((A, \rho) .\) (For brevity, we omit the centers and radii; we also omit the trivial case \(G=\emptyset .\)
\[G=\bigcup_{i} G_{i}^{*}=\bigcup_{i}\left(A \cap G_{i}\right)=A \cap \bigcup_{i} G_{i},\]
by set theory (see Chapter 1, §§1-3,\) Problem 9).
Again by Corollary \(1, U=\bigcup_{i} G_{i}\) is an open set in \((S, \rho) .\) Thus \(G\) has the form
\[A \cap \bigcup_{i} G_{i}=A \cap U,\]
with \(U\) open in \(S,\) as asserted.
Conversely, assume the latter, and let \(p \in G .\) Then \(p \in A\) and \(p \in U .\) As \(U\) is open in \((S, \rho),\) there is a globe \(G_{p}\) in \((S, \rho)\) such that \(p \in G_{p} \subseteq U .\) As \(p \in A,\) we have
\[p \in A \cap G_{p} \subseteq A \cap U.\]
However, \(A \cap G_{p}\) is a globe in \((A, \rho),\) call it \(G_{p}^{*} .\) Thus
\[p \in G_{p}^{*} \subseteq A \cap U=G;\]
i.e., \(p\) is an interior point of \(G\) in \((A, \rho) .\) We see that each \(p \in G\) is interior to \(G,\) as a set in \((A, \rho),\) so \(G\) is open in \((A, \rho) .\)
This proves the theorem for open sets. Now let \(F\) be closed in \((A, \rho) .\) Then by Definition \(3, A-F\) is open in \((A, \rho) .\) (Of course, when working in \((A, \rho)\), we replace \(S\) by \(A\) in taking complements.) Let \(G=A-F,\) so \(F=A-G,\) and \(G\) is open in \((A, \rho) .\) By what was shown above, \(G=A \cap U\) with \(U\) open in \(S\).
Thus
\[F=A-G=A-(A \cap U)=A-U=A \cap(-U)\]
by set theory. Here \(-U=S-U\) is closed in \((S, \rho)\) since \(U\) is open there. Thus \(F=A \cap(-U),\) as required.
The proof of the converse (for closed sets) is left as an exercise. \(\square\)


